《2025年5年中考3年模拟九年级数学上册华师大版》

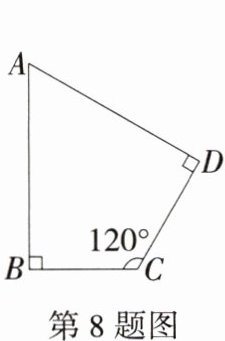
8.[2025福建泉州晋江养正中学一模,★☆]如图,在四边形ABCD中,$∠C= 120^{\circ },∠B= ∠D= 90^{\circ },BC= 2,CD= 3$,则$AB= $( )

A.$\frac {8\sqrt {3}}{3}$
B.5
C.4
D.$2\sqrt {3}$

答案：
A 如图，延长AD，BC交于点E，
∵∠BCD = 120°，∠B = ∠ADC = 90°，
∴∠A = 60°，
∴∠E = 30°，
∵CD = 3，
∴CE = 6，又
∵BC = 2，
∴BE = BC + CE = 8，在Rt△ABE中，∠E = 30°，设AB = x，则AE = 2x，由勾股定理可得(2x)² - x² = 8²，解得x = $\frac{8\sqrt{3}}{3}$（舍负），即AB = $\frac{8\sqrt{3}}{3}$。

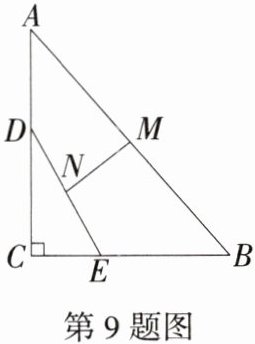
9.[2025四川巴中一模,★☆]如图,在$△ABC$中,$∠C= 90^{\circ },AC= 8,BC= 6$,线段DE的两个端点D、E分别在边AC、BC上移动,且$DE= 6$,若点M、N分别是AB、DE的中点,则MN的最小值为( )

A.2
B.3
C.3.5
D.4

答案：
A 如图，连结CM、CN，
∵在△ABC中，∠ACB = 90°，AC = 8，BC = 6，
∴AB = $\sqrt{AC^2 + BC^2}$ = 10，
∵DE = 6，点M、N分别是AB、DE的中点，
∴CN = $\frac{1}{2}$DE = 3，CM = $\frac{1}{2}$AB = 5，当C、M、N在同一直线上时，MN取得最小值，MN的最小值为5 - 3 = 2。

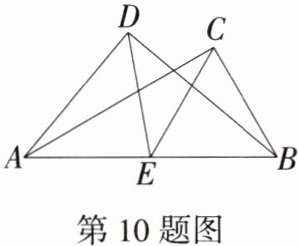
10.[2025福建泉州安溪二模,★☆]如图,在$Rt△ABD和Rt△ABC$中,$∠ADB= ∠ACB= 90^{\circ },∠CAB= 30^{\circ },∠DBA= 40^{\circ }$,E是AB的中点,则$∠DEC=$____40$^{\circ }$.

答案： 答案 40
解析
∵∠ADB = ∠ACB = 90°，∠CAB = 30°，∠DBA = 40°，
∴∠ABC = 60°，∠BAD = 50°，
∵在Rt△ABD和Rt△ABC中，E是AB的中点，
∴DE = AE = CE = BE，
∴∠BCE = ∠ABC = 60°，∠ADE = ∠BAD = 50°，
∴∠CEB = 180° - ∠BCE - ∠ABC = 60°，∠AED = 180° - ∠ADE - ∠BAD = 80°，
∴∠DEC = 180° - 60° - 80° = 40°。

11.学科分类讨论[2024新疆中考,★☆]如图,在$Rt△ABC$中,$∠C= 90^{\circ },∠A= 30^{\circ },AB= 8$.若点D在直线AB上(不与点A,B重合),且$∠BCD= 30^{\circ }$,则AD的长为____.

答案：
答案 6或12
解析
∵在Rt△ABC中，∠ACB = 90°，∠A = 30°，AB = 8，
∴BC = $\frac{1}{2}$×8 = 4，
∴AC = $\sqrt{8^2 - 4^2}$ = 4$\sqrt{3}$，分情况讨论如下：
（1）当点D在AB的延长线上时，如图1所示，
∵∠ACB = 90°，∠A = 30°，
∴∠ABC = 60°。
∵∠BCD = 30°，
∴∠BDC = 60° - 30° = 30°，
∴BD = BC = 4，
∴AD = 8 + 4 = 12。

（2）当点D在AB上时，如图2所示，
∵∠ABC = 60°，∠BCD = 30°，
∴∠CDA = 90°。
∵在Rt△ACD中，∠A = 30°，
∴CD = $\frac{1}{2}$×4$\sqrt{3}$ = 2$\sqrt{3}$，
∴AD = $\sqrt{AC^2 - CD^2}$ = $\sqrt{(4\sqrt{3})^2 - (2\sqrt{3})^2}$ = 6。
综上所述，AD的长为6或12。

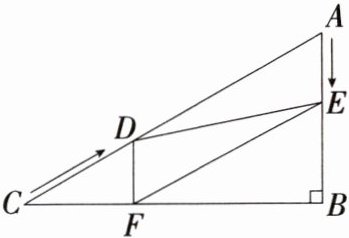
12.新考向动点探究题[2024福建泉州洛江二模,★☆]如图,在$Rt△ABC$中,$∠B= 90^{\circ },AC= 60cm,∠A= 60^{\circ }$,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D,E运动的时间是t秒$(0＜t≤15)$.过点D作$DF⊥BC$于点F,连结DE,EF.
(1)求证:$AE= DF$.
(2)当t为何值时,$△DEF$为直角三角形?请说明理由.

(1)证明：∵在Rt△ABC中，∠B = 90°，∠A = 60°，∴∠C = 90° - ∠A = 30°。∵在Rt△CDF中，∠C = 30°，CD = 4t cm，∴DF = $\frac{1}{2}$CD = 2t cm，∵点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，∴AE = 2t cm，∴AE = DF。
(2)分情况讨论如下：
①当∠DEF = 90°时，由（1）易知四边形AEFD为平行四边形，∴EF//AD，∴∠ADE = ∠DEF = 90°，∵∠A = 60°，∴∠AED = 30°，∴AD = $\frac{1}{2}$AE = t cm，∵AD = (60 - 4t)cm，∴60 - 4t = t，解得t = 12。
②当∠EDF = 90°时，四边形EBFD为矩形，∴∠AED = 90°，∵在Rt△AED中，∠A = 60°，则∠ADE = 30°，∴AD = 2AE = 4t cm，∴60 - 4t = 4t，解得t = $\frac{15}{2}$。
③不存在∠EFD = 90°的情况。
综上所述，当t = $\frac{15}{2}$或12时，△DEF为直角三角形。

答案： 解析 （1）证明：
∵在Rt△ABC中，∠B = 90°，∠A = 60°，
∴∠C = 90° - ∠A = 30°。
∵在Rt△CDF中，∠C = 30°，CD = 4t cm，
∴DF = $\frac{1}{2}$CD = 2t cm，
∵点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动，
∴AE = 2t cm，
∴AE = DF。
（2）分情况讨论如下：
①当∠DEF = 90°时，由（1）易知四边形AEFD为平行四边形，
∴EF//AD，
∴∠ADE = ∠DEF = 90°，
∵∠A = 60°，
∴∠AED = 30°，
∴AD = $\frac{1}{2}$AE = t cm，
∵AD = (60 - 4t)cm，
∴60 - 4t = t，解得t = 12。
②当∠EDF = 90°时，四边形EBFD为矩形，
∴∠AED = 90°，
∵在Rt△AED中，∠A = 60°，则∠ADE = 30°，
∴AD = 2AE = 4t cm，
∴60 - 4t = 4t，解得t = $\frac{15}{2}$。
③不存在∠EFD = 90°的情况。
综上所述，当t = $\frac{15}{2}$或12时，△DEF为直角三角形。

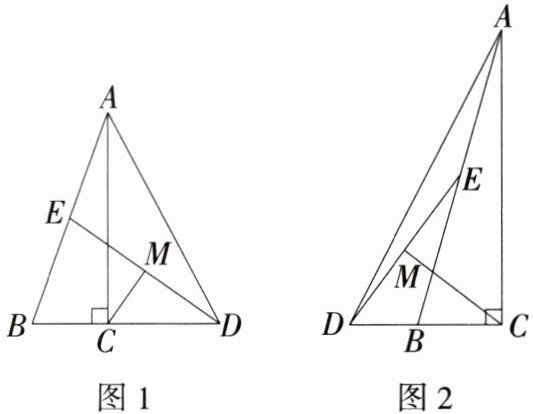
13.新课标推理能力[2025河南新乡原阳期末]如图1,已知$△ABC$为直角三角形,$∠ACB= 90^{\circ }$,在BC的延长线上取一点D,使得$CD= \frac {1}{2}AB$,点E是AB的中点,连结DE,M为ED的中点,连结CM、AD.
(1)试判断CM是否垂直平分ED,并说明理由.
(2)若$∠AED= 105^{\circ }$,请求出$∠BAC$的度数.
(3)如果将题中“在BC的延长线上取一点D”改为“在CB的延长线上取一点D”,其余条件不变,如图2,若$∠AED= 165^{\circ }$,请求出$∠BAC$的度数.

答案：
解析 （1）CM垂直平分ED。理由如下：如图1，连结CE，
∵∠ACB = 90°，点E是AB的中点，
∴AB = 2CE，
∵CD = $\frac{1}{2}$AB，
∴CE = CD，
∵M为ED的中点，
∴CM垂直平分ED。


（2）如图1，
∵∠ACB = 90°，点E是AB的中点，
∴BE = CE = $\frac{1}{2}$AB，
∴∠B = ∠ECB，
∵CE = CD，
∴∠CDE = ∠DEC，
∴∠ECB = ∠DEC + ∠CDE = 2∠CDE，
∴∠B = 2∠CDE，
∵∠AED = ∠B + ∠CDE，
∴∠AED = 3∠CDE，
∵∠AED = 105°，
∴∠CDE = 35°，
∴∠B = 70°，
∵∠ACB = 90°，
∴∠BAC = 180° - 90° - 70° = 20°。
（3）如图2，连结CE，
∵∠ACB = 90°，点E是AB的中点，
∴AB = 2CE，BE = CE，
∴∠EBC = ∠ECB，
∵CD = $\frac{1}{2}$AB，
∴CE = CD，
∴∠CDE = ∠DEC，
∵∠AED = 165°，
∴∠BED = 180° - 165° = 15°，
∵∠EBC = ∠CDE + ∠BED，
∴∠ECB = ∠EBC = ∠CDE + 15°，
∵∠AED = ∠CDE + ∠DBE，∠DBE = ∠ECB + ∠CEB，
∴∠AED = ∠CDE + ∠ECB + ∠CEB，
∵∠CEB = ∠CED - ∠BED，
∴∠CEB = ∠CDE - 15°，
∴∠AED = ∠CDE + ∠CDE + 15° + ∠CDE - 15° = 3∠CDE，
∴∠CDE = 55°，
∴∠EBC = 55° + 15° = 70°，
∴∠BAC = 180° - 90° - 70° = 20°。