第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
1.「2025 山东烟台龙口期中」用计算器求 $\sin 24^{\circ} 37^{\prime} 18^{\prime \prime}$ 的值,下列按键顺序正确的是 (
A
)
答案:
A 先按“sin”键,再输入角的度数,按“=”键即可得到结果.
2.「2025 山东淄博临淄期末」利用科学计算器按顺序输入: $\mathrm{SHIFT} \tan 36 \cdot 79= $, 显示屏显示的结果为 88.443 009 64. 将这个数据精确到 0.1 后,下列说法正确的是 (
A. $36.79^{\circ}$ 角的正切值约为 88.4
B. 正切值为 36.79 的角的度数约是 $88.4^{\circ}$
C. $36^{\circ} 79^{\prime}$ 角的正切值约为 88.4
D. 正切值为 36.79 的角的度数约是 $88^{\circ} 4^{\prime}$
B
)A. $36.79^{\circ}$ 角的正切值约为 88.4
B. 正切值为 36.79 的角的度数约是 $88.4^{\circ}$
C. $36^{\circ} 79^{\prime}$ 角的正切值约为 88.4
D. 正切值为 36.79 的角的度数约是 $88^{\circ} 4^{\prime}$
答案:
B 根据计算器的使用方法可知,正切值为36.79的角的度数约是88.4°.
3.「2025 吉林长春净月实验学校月考」在 $\mathrm{Rt} \triangle A B C$ 中, $\angle C$ $=90^{\circ}, A C= 8, A B= 2 \sqrt{19}$, 则 $\angle A$ 的度数约为
23.4°
. (精确到 $0.1^{\circ}$ )
答案:
答案 23.4°
解析 根据题意可知$\cos A = \frac{AC}{AB} = \frac{8}{2\sqrt{19}} \approx 0.918$,
$\therefore \angle A \approx 23.4^{\circ}$。
解析 根据题意可知$\cos A = \frac{AC}{AB} = \frac{8}{2\sqrt{19}} \approx 0.918$,
$\therefore \angle A \approx 23.4^{\circ}$。
4.「2025 福建泉州泉港二模改编」如图, 某厂房屋顶人字架的跨度 $B C= 16 \mathrm{~m}$, 上弦 $A B= A C, \angle B A C= $ $130^{\circ}$, 则用科学计算器可得上弦 $A B$ 的长是 m. (结果精确到 0.01 )

答案:
答案 8.83
解析 如图,作$AD \perp BC$于点$D$。$\because AB = AC$,$\therefore \triangle ABC$是等腰三角形,$\because AD \perp BC$,$\therefore BD = \frac{1}{2}BC$,$\angle BAD = \frac{1}{2}\angle BAC$,$\because BC = 16m$,$\angle BAC = 130^{\circ}$,$\therefore BD = 8m$,$\angle BAD = 65^{\circ}$,$\because \sin \angle BAD = \frac{BD}{AB}$,
$\therefore AB = BD \div \sin \angle BAD = 8 \div \sin 65^{\circ} \approx 8.83(m)$。

答案 8.83
解析 如图,作$AD \perp BC$于点$D$。$\because AB = AC$,$\therefore \triangle ABC$是等腰三角形,$\because AD \perp BC$,$\therefore BD = \frac{1}{2}BC$,$\angle BAD = \frac{1}{2}\angle BAC$,$\because BC = 16m$,$\angle BAC = 130^{\circ}$,$\therefore BD = 8m$,$\angle BAD = 65^{\circ}$,$\because \sin \angle BAD = \frac{BD}{AB}$,
$\therefore AB = BD \div \sin \angle BAD = 8 \div \sin 65^{\circ} \approx 8.83(m)$。

5. 用计算器求下列各式的值 (精确到 0.0001 ):
(1) $\cos 78^{\circ} 33^{\prime} 52^{\prime \prime} \cdot \tan 50^{\circ} 36^{\prime}$.
(2) $\sin 8.7^{\circ}-\cos 54^{\circ} 3^{\prime \prime}+\sqrt{7} \tan 63^{\circ} 27^{\prime}$.
(1) $\cos 78^{\circ} 33^{\prime} 52^{\prime \prime} \cdot \tan 50^{\circ} 36^{\prime}$.
(2) $\sin 8.7^{\circ}-\cos 54^{\circ} 3^{\prime \prime}+\sqrt{7} \tan 63^{\circ} 27^{\prime}$.
答案:
解析
(1)原式$\approx 0.2414$。
(2)原式$\approx 4.8585$。
(1)原式$\approx 0.2414$。
(2)原式$\approx 4.8585$。
6. 教材变式「2024 陕西咸阳实验中学一模, 」若三个锐角 $\alpha, \beta, \gamma$ 满足 $\sin \alpha=0.848, \cos \beta=0.454, \tan \gamma$ $=1.804$, 则 $\alpha, \beta, \gamma$ 的大小关系为 (
A. $\beta<\alpha<\gamma$
B. $\alpha<\beta<\gamma$
C. $\alpha<\gamma<\beta$
D. $\beta<\gamma<\alpha$
C
)A. $\beta<\alpha<\gamma$
B. $\alpha<\beta<\gamma$
C. $\alpha<\gamma<\beta$
D. $\beta<\gamma<\alpha$
答案:
C 利用计算器进行计算,$\sin \alpha = 0.848$,则$\alpha \approx 58^{\circ}$;$\cos \beta = 0.454$,则$\beta \approx 63^{\circ}$;$\tan \gamma = 1.804$,则$\gamma \approx 61^{\circ}$。故$\alpha < \gamma < \beta$。
7.「2025 湖南衡阳祁东二模, 」用计算器验证, 下列不等式中成立的是 (
A. $\sin 36^{\circ} 24^{\prime}>\cos 37^{\circ} 24^{\prime}+\cos 3^{\circ} 10^{\prime}$
B. $\cos 45^{\circ} 32^{\prime}>\sin 45^{\circ}-\sin 1^{\circ} 12^{\prime}$
C. $\sin 63^{\circ} 47^{\prime}<\cos 18^{\circ} 21^{\prime}-\cos 87^{\circ}$
D. $2 \sin 30^{\circ} 12^{\prime}<\sin 60^{\circ} 24^{\prime}$
B
)A. $\sin 36^{\circ} 24^{\prime}>\cos 37^{\circ} 24^{\prime}+\cos 3^{\circ} 10^{\prime}$
B. $\cos 45^{\circ} 32^{\prime}>\sin 45^{\circ}-\sin 1^{\circ} 12^{\prime}$
C. $\sin 63^{\circ} 47^{\prime}<\cos 18^{\circ} 21^{\prime}-\cos 87^{\circ}$
D. $2 \sin 30^{\circ} 12^{\prime}<\sin 60^{\circ} 24^{\prime}$
答案:
B 利用计算器分别对各选项进行计算,根据计算结果进行验证即可。
8.「2025 福建漳州长泰期末, 」已知 $\alpha$ 为锐角, 且 $\tan \alpha=1.385$, 则 $\sin \alpha \approx$
0.8108
, $\cos \alpha \approx$0.5854
. (精确到 0.0001 )
答案:
答案 0.8108;0.5854
解析 用计算器算得$\alpha \approx 54.17^{\circ}$,则$\sin \alpha \approx 0.8108$,$\cos \alpha \approx 0.5854$。
解析 用计算器算得$\alpha \approx 54.17^{\circ}$,则$\sin \alpha \approx 0.8108$,$\cos \alpha \approx 0.5854$。
9. 运算能力「2025 山东东营垦利期中」
(1) 通过用计算器计算, 比较下列各对数的大小, 并提出你的猜想:
(1) $\sin 36^{\circ}$
(2) $\sin 45^{\circ}$
(3) $\sin 80^{\circ}$
猜想: 已知 $0^{\circ}<\alpha<45^{\circ}$, 则 $\sin 2 \alpha$
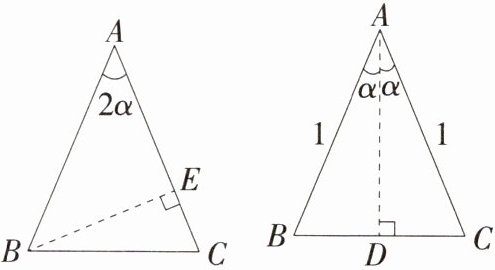
(2) 如图, 在 $\triangle A B C$ 中, $A B= A C= 1, \angle B A C= 2 \alpha$, 请根据图中提示, 利用面积法验证结论.
(1) 通过用计算器计算, 比较下列各对数的大小, 并提出你的猜想:
(1) $\sin 36^{\circ}$
=
$2 \sin 18^{\circ} \cdot \cos 18^{\circ}$;(2) $\sin 45^{\circ}$
=
$2 \sin 22.5^{\circ} \cdot \cos 22.5^{\circ}$;(3) $\sin 80^{\circ}$
=
$2 \sin 40^{\circ} \cdot \cos 40^{\circ}$.猜想: 已知 $0^{\circ}<\alpha<45^{\circ}$, 则 $\sin 2 \alpha$
=
$2 \sin \alpha \cdot \cos \alpha$.(2) 如图, 在 $\triangle A B C$ 中, $A B= A C= 1, \angle B A C= 2 \alpha$, 请根据图中提示, 利用面积法验证结论.

答案:
解析
(1)①$\sin 36^{\circ} = 2\sin 18^{\circ} \cdot \cos 18^{\circ}$。
②$\sin 45^{\circ} = 2\sin 22.5^{\circ} \cdot \cos 22.5^{\circ}$。
③$\sin 80^{\circ} = 2\sin 40^{\circ} \cdot \cos 40^{\circ}$。
猜想:已知$0^{\circ} < \alpha < 45^{\circ}$,则$\sin 2\alpha = 2\sin \alpha \cdot \cos \alpha$。
(2)证明:$\because S_{\triangle ABC} = \frac{1}{2}AC \cdot BE = \frac{1}{2}AC \cdot AB \cdot \sin 2\alpha = \frac{1}{2}\sin 2\alpha$,$S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = \frac{1}{2} \times 2AB \cdot \sin \alpha \cdot AC \cdot \cos \alpha = \sin \alpha \cdot \cos \alpha$,$\therefore \sin 2\alpha = 2\sin \alpha \cdot \cos \alpha$。
(1)①$\sin 36^{\circ} = 2\sin 18^{\circ} \cdot \cos 18^{\circ}$。
②$\sin 45^{\circ} = 2\sin 22.5^{\circ} \cdot \cos 22.5^{\circ}$。
③$\sin 80^{\circ} = 2\sin 40^{\circ} \cdot \cos 40^{\circ}$。
猜想:已知$0^{\circ} < \alpha < 45^{\circ}$,则$\sin 2\alpha = 2\sin \alpha \cdot \cos \alpha$。
(2)证明:$\because S_{\triangle ABC} = \frac{1}{2}AC \cdot BE = \frac{1}{2}AC \cdot AB \cdot \sin 2\alpha = \frac{1}{2}\sin 2\alpha$,$S_{\triangle ABC} = \frac{1}{2}BC \cdot AD = \frac{1}{2} \times 2AB \cdot \sin \alpha \cdot AC \cdot \cos \alpha = \sin \alpha \cdot \cos \alpha$,$\therefore \sin 2\alpha = 2\sin \alpha \cdot \cos \alpha$。
查看更多完整答案,请扫码查看


