《2025年5年中考3年模拟九年级数学上册华师大版》

1. 「2023江苏无锡中考」$\cos 60^{\circ}$的值为 (B)
A. $\frac{\sqrt{3}}{2}$
B. $\frac{1}{2}$
C. $\frac{\sqrt{3}}{3}$
D. $\sqrt{3}$

答案： B　cos60°=$\frac{1}{2}$.

2. 「2025河南南阳邓州期末」若$\tan (\alpha - 10^{\circ}) = 1$,则锐角$\alpha$的度数是 (C)
A. $40^{\circ}$
B. $35^{\circ}$
C. $55^{\circ}$
D. $70^{\circ}$

答案： C
∵tan(α−10°)=1,tan45°=1,
∴α−10°=45°,解得α=55°.

3. 「2025甘肃金昌永昌七中二楼」在$\triangle ABC$中,$\angle A$,$\angle B$是锐角,且$\sin A = \frac{\sqrt{2}}{2}$,$\cos B = \frac{1}{2}$,则$\triangle ABC$的形状是 (C)
A. 直角三角形
B. 钝角三角形
C. 锐角三角形
D. 锐角三角形或钝角三角形

答案： C
∵sinA=$\frac{\sqrt{2}}{2}$,cosB=$\frac{1}{2}$,
∴∠A=45°,∠B=60°,
∴∠C=75°,
∴△ABC是锐角三角形.

4. 在$\triangle ABC$中,已知$\angle A$,$\angle B$是锐角,若$|3\tan A - \sqrt{3}| + (2\cos B - \sqrt{3})^2 = 0$,则$\angle C$的度数为______120°.

答案： 答案　120°
解析
∵|3tanA - $\sqrt{3}$|+(2cosB - $\sqrt{3}$)²=0,
∴3tanA - $\sqrt{3}$=0,2cosB - $\sqrt{3}$=0,
∴tanA=$\frac{\sqrt{3}}{3}$,cosB=$\frac{\sqrt{3}}{2}$,
∴∠A=30°,∠B=30°,
∴∠C=180°−∠A−∠B=120°.

5. 学科易错题「2024黑龙江哈尔滨中考」$\triangle ABC$是直角三角形,$AB = 2\sqrt{3}$,$\angle ABC = 30^{\circ}$,则$AC$的长为2或$\sqrt{3}$.

答案： 答案　2或$\sqrt{3}$
解析　分情况求解如下:
(1) 若∠A=90°,则tan∠ABC=$\frac{AC}{AB}$=$\frac{\sqrt{3}}{3}$,
∵AB=2$\sqrt{3}$,
∴AC=$\frac{\sqrt{3}}{3}$AB=2;
(2) 若∠C=90°,则sin∠ABC=$\frac{AC}{AB}$=$\frac{1}{2}$,
∵AB=2$\sqrt{3}$,
∴AC=$\frac{1}{2}$AB=$\sqrt{3}$.
综上所述,AC的长为2或$\sqrt{3}$.
易错警示　本题易受思维定式的影响而认为∠C=90°,漏掉了∠A=90°的情况.

6. 计算：
(1)$2\sin 30^{\circ} + \tan 45^{\circ} + \cos^2 30^{\circ} - \sin^2 45^{\circ}$.
(2)$6\tan^2 30^{\circ} - \cos 30^{\circ} \cdot \tan 60^{\circ} - 2\sin 45^{\circ} + \cos 60^{\circ}$.
(3)$\cos^2 45^{\circ} - \tan 60^{\circ} \cdot \tan 30^{\circ} + |\sin 60^{\circ} - 1| - (-\tan 45^{\circ})^{2023}$.

答案： 解析　
(1) 原式=2×$\frac{1}{2}$+1+($\frac{\sqrt{3}}{2}$)² - ($\frac{\sqrt{2}}{2}$)²=1+1+$\frac{3}{4}$ - $\frac{1}{2}$=$\frac{9}{4}$.
(2) 原式=6×($\frac{\sqrt{3}}{3}$)² - $\frac{\sqrt{3}}{2}$×$\sqrt{3}$ - 2×$\frac{\sqrt{2}}{2}$+$\frac{1}{2}$=2 - $\frac{3}{2}$ - $\sqrt{2}$+$\frac{1}{2}$=1 - $\sqrt{2}$.
(3) 原式=($\frac{\sqrt{2}}{2}$)² - $\sqrt{3}$×$\frac{\sqrt{3}}{3}$+1 - $\frac{\sqrt{3}}{2}$ - (-1)²⁰²³=$\frac{1}{2}$ - 1+1 - $\frac{\sqrt{3}}{2}$+1=$\frac{3}{2}$ - $\frac{\sqrt{3}}{2}$.

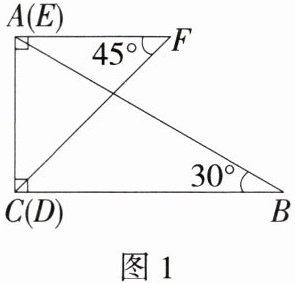
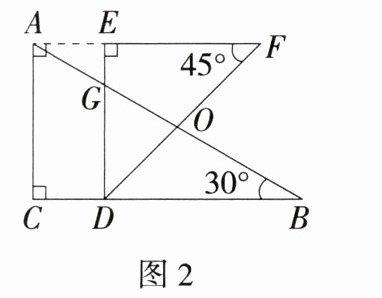
7. 「2025甘肃天水甘谷一模,★☆」如图1,将三角尺$ABC和三角尺DEF$叠放在一起,直角边$AC与DE$完全重合,已知$AB的长为16\mathrm{cm}$。若三角尺$DEF沿CB$方向移动到图2的位置,此时测得$OB的长为6\mathrm{cm}$,则移动距离$CD$为 ( )

A. $2\mathrm{cm}$
B. $5\sqrt{3}\mathrm{cm}$
C. $(5\sqrt{3} - 3)\mathrm{cm}$
D. $(8\sqrt{3} - 5)\mathrm{cm}$

答案：
C　如图,过点O作OH⊥BC于点H,
∵∠ACB=90°,AB=16cm,∠B=30°,
∴BC=AB·cos30°=16×$\frac{\sqrt{3}}{2}$=8$\sqrt{3}$(cm),
∵OB=6cm,
∴BH=OB·cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$(cm),OH=$\frac{1}{2}$OB=$\frac{1}{2}$×6=3(cm),
∵∠EDF=∠FDB=45°,∠OHD=90°,
∴DH=OH=3(cm),
∴CD=BC−DH−HB=8$\sqrt{3}$ - 3 - 3$\sqrt{3}$=(5$\sqrt{3}$ - 3)cm.

8. 「2024四川广元二模,★☆」已知$a$,$b$,$c是\triangle ABC$三边的长,$b ＞ a = c$,且方程$ax^2 - \sqrt{2}bx + c = 0的两根的差的绝对值等于\sqrt{2}$,则$\triangle ABC$中最大角的度数是 ( )
A. $150^{\circ}$
B. $120^{\circ}$
C. $90^{\circ}$
D. $60^{\circ}$

答案：
B　设x₁、x₂是方程ax² - $\sqrt{2}$bx + c = 0的两根,则x₁ + x₂ = $\frac{\sqrt{2}b}{a}$,x₁x₂ = $\frac{c}{a}$,
∵|x₁ - x₂| = $\sqrt{2}$,
∴(x₁ - x₂)² = 2,即(x₁ + x₂)² - 4x₁x₂ = 2,
∴$\frac{2b²}{a²}$ - $\frac{4c}{a}$ = 2.
∵a = c,
∴$\frac{2b²}{c²}$ - 4 = 2,即$\frac{b²}{c²}$ = 3,
∴$\frac{b}{c}$ = $\sqrt{3}$(负值已舍去).根据题意画出示意图如图,过点B作BD⊥AC于点D,
∵a = c,
∴AD = $\frac{b}{2}$,∠ABD = $\frac{1}{2}$∠ABC,
∴sin∠ABD = $\frac{AD}{AB}$ = $\frac{\frac{b}{2}}{c}$ = $\frac{1}{2}$·$\frac{b}{c}$ = $\frac{\sqrt{3}}{2}$,
∴∠ABD = 60°,
∴∠ABC = 2∠ABD = 120°.

9. 「2025湖南衡阳蒸湘一模,★☆」若$\angle A$为锐角,且满足$\sin^2 A + \frac{1}{2} = \frac{3}{2}\sin A$,则$\angle A$的度数为30°.

答案： 答案　30°
解析
∵sin²A + $\frac{1}{2}$ = $\frac{3}{2}$sinA,
∴sinA = $\frac{1}{2}$或sinA = 1,
∵∠A为锐角,
∴sinA = $\frac{1}{2}$,
∴∠A的度数为30°.

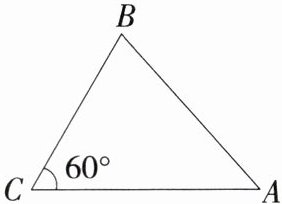
10. 「2024河南周口沈丘二模,★☆」如图,在$\triangle ABC$中,$AC = 8$,$BC = 6$,$\angle C = 60^{\circ}$,求$AB$的长.

答案：
解析　如图,作BD⊥AC,垂足为D,
∴∠BDC = ∠BDA = 90°,
∵在Rt△BDC中,BC = 6,∠C = 60°,
∴CD = BC·cos60° = 6×$\frac{1}{2}$ = 3,BD = BC·sin60° = 6×$\frac{\sqrt{3}}{2}$ = 3$\sqrt{3}$,
∵AC = 8,
∴AD = AC - CD = 5,
∴在Rt△ABD中,AB = $\sqrt{AD² + BD²}$ = $\sqrt{5² + (3\sqrt{3})²}$ = 2$\sqrt{13}$,即AB的长为2$\sqrt{13}$.