第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
11.「2024吉林长春宽城二模,」小丽与小霞两位同学解方程$3(x-3)= (x-3)^{2}$的过程如下:
小丽:
方程两边同除以$(x-3)$,得$3= x-3$,
解得$x= 6$
小霞:
移项,得$3(x-3)-(x-3)^{2}= 0$,
提取公因式,得$(x-3)\cdot (3-x-3)= 0$,
所以$x-3= 0或3-x-3= 0$,
解得$x_{1}= 3,x_{2}= 0$
(1)你认为她们的解法是否正确?若正确,请在框内打“√”;若错误,请在框内打“×”,并写出你的解答过程.
正确的解答过程如下:移项,得$3(x - 3) - (x - 3)^2 = 0$,提取公因式,得$(x - 3)(3 - x + 3) = 0$,所以$x - 3 = 0$或$6 - x = 0$,解得$x_1 = 3$,$x_2 = 6$。
(2)请结合上述题目总结形如$ax^{2}= bx(a≠0)$的一元二次方程的一般解法.
小丽:
方程两边同除以$(x-3)$,得$3= x-3$,
解得$x= 6$
小霞:
移项,得$3(x-3)-(x-3)^{2}= 0$,
提取公因式,得$(x-3)\cdot (3-x-3)= 0$,
所以$x-3= 0或3-x-3= 0$,
解得$x_{1}= 3,x_{2}= 0$
(1)你认为她们的解法是否正确?若正确,请在框内打“√”;若错误,请在框内打“×”,并写出你的解答过程.
×
×
正确的解答过程如下:移项,得$3(x - 3) - (x - 3)^2 = 0$,提取公因式,得$(x - 3)(3 - x + 3) = 0$,所以$x - 3 = 0$或$6 - x = 0$,解得$x_1 = 3$,$x_2 = 6$。
(2)请结合上述题目总结形如$ax^{2}= bx(a≠0)$的一元二次方程的一般解法.
移项,得$ax^2 - bx = 0$,提取公因式,得$x(ax - b) = 0$,所以$x = 0$或$ax - b = 0$,解得$x_1 = 0$,$x_2 = \frac{b}{a}$
答案:
解析
(1) 她们的解法都不正确,正确的解答过程如下:移项,得 $ 3(x - 3) - (x - 3)^2 = 0 $,提取公因式,得 $ (x - 3)(3 - x + 3) = 0 $,所以 $ x - 3 = 0 $ 或 $ 6 - x = 0 $,解得 $ x_1 = 3 $,$ x_2 = 6 $。
(2) 形如 $ ax^2 = bx(a ≠ 0) $ 的一元二次方程的一般解法:移项,得 $ ax^2 - bx = 0 $,提取公因式,得 $ x(ax - b) = 0 $,所以 $ x = 0 $ 或 $ ax - b = 0 $,解得 $ x_1 = 0 $,$ x_2 = \frac{b}{a} $。
(1) 她们的解法都不正确,正确的解答过程如下:移项,得 $ 3(x - 3) - (x - 3)^2 = 0 $,提取公因式,得 $ (x - 3)(3 - x + 3) = 0 $,所以 $ x - 3 = 0 $ 或 $ 6 - x = 0 $,解得 $ x_1 = 3 $,$ x_2 = 6 $。
(2) 形如 $ ax^2 = bx(a ≠ 0) $ 的一元二次方程的一般解法:移项,得 $ ax^2 - bx = 0 $,提取公因式,得 $ x(ax - b) = 0 $,所以 $ x = 0 $ 或 $ ax - b = 0 $,解得 $ x_1 = 0 $,$ x_2 = \frac{b}{a} $。
12.规律探究题「2025四川巴中二模,」将一些棋子按如图所示的方式摆放:

第1个图中有6个棋子,第2个图中有10个棋子,第3个图中有16个棋子,……,按此规律依次递增.
(1)第5个图中有
(2)第n个图中有
(3)如果第n个图中有114个棋子,求出n的值.

第1个图中有6个棋子,第2个图中有10个棋子,第3个图中有16个棋子,……,按此规律依次递增.
(1)第5个图中有
34
个棋子.(2)第n个图中有
n²+n+4
个棋子.(3)如果第n个图中有114个棋子,求出n的值.
10
答案:
解析
(1) 第 5 个图中有 $ 4 + 5×(5 + 1) = 4 + 30 = 34 $ 个棋子。
(2) 第 $ n $ 个图中有 $ 4 + n(n + 1) = (n^2 + n + 4) $ 个棋子。
(3) 由题意得 $ n^2 + n + 4 = 114 $,整理得 $ (n - 10)(n + 11) = 0 $,解得 $ n = 10 $ 或 $ n = -11 $(不合题意,舍去),
∴ $ n $ 的值为 10。
(1) 第 5 个图中有 $ 4 + 5×(5 + 1) = 4 + 30 = 34 $ 个棋子。
(2) 第 $ n $ 个图中有 $ 4 + n(n + 1) = (n^2 + n + 4) $ 个棋子。
(3) 由题意得 $ n^2 + n + 4 = 114 $,整理得 $ (n - 10)(n + 11) = 0 $,解得 $ n = 10 $ 或 $ n = -11 $(不合题意,舍去),
∴ $ n $ 的值为 10。
13.运算能力「2025四川资阳雁江期中改编」我们知道可以用公式$x^{2}+(p+q)x+pq= (x+p)(x+q)$来分解因式,从而解一元二次方程.
例如:$x^{2}+6x+8= 0$,方程分解得
爱钻研的小明同学发现二次项系数不是1的方程也可以借助此方法解.
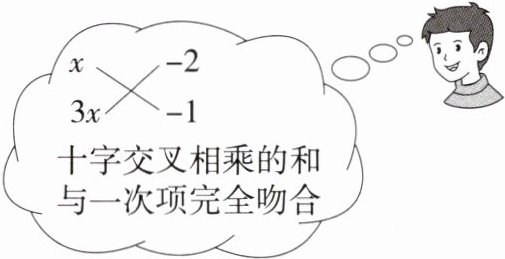
例如:$3x^{2}-7x+2= 0$.
解:方程分解为$(x-2)(3x-1)= 0$,从而可以快速求出方程的解.
(1)补全题中空白部分的内容.
(2)请利用此方法解方程$4x^{2}-8x-5= 0$.
解:分解因式,得
(3)请利用此方法解关于x的一元二次方程$3x^{2}-(6+a)x+2a= 0$.
解:分解因式,得
例如:$x^{2}+6x+8= 0$,方程分解得
$(x + 2)(x + 4)$
= 0,$x^{2}-7x-30= 0$,方程分解得$(x - 10)(x + 3)$
= 0.爱钻研的小明同学发现二次项系数不是1的方程也可以借助此方法解.
例如:$3x^{2}-7x+2= 0$.
解:方程分解为$(x-2)(3x-1)= 0$,从而可以快速求出方程的解.

(1)补全题中空白部分的内容.
(2)请利用此方法解方程$4x^{2}-8x-5= 0$.
解:分解因式,得
$(2x - 5)(2x + 1)$
= 0,∴$2x - 5 = 0$
或$2x + 1 = 0$
,解得$x_1 = \frac{5}{2}$,$x_2 = -\frac{1}{2}$
。(3)请利用此方法解关于x的一元二次方程$3x^{2}-(6+a)x+2a= 0$.
解:分解因式,得
$(3x - a)(x - 2)$
= 0,∴$3x - a = 0$
或$x - 2 = 0$
,解得$x_1 = \frac{a}{3}$,$x_2 = 2$
。
答案:
解析
(1) $ (x + 2)(x + 4) $;$ (x - 10)(x + 3) $。
(2) 分解因式,得 $ (2x - 5)(2x + 1) = 0 $,
∴ $ 2x - 5 = 0 $ 或 $ 2x + 1 = 0 $,解得 $ x_1 = \frac{5}{2} $,$ x_2 = -\frac{1}{2} $。
(3) 分解因式,得 $ (3x - a)(x - 2) = 0 $,
∴ $ 3x - a = 0 $ 或 $ x - 2 = 0 $,解得 $ x_1 = \frac{a}{3} $,$ x_2 = 2 $。
(1) $ (x + 2)(x + 4) $;$ (x - 10)(x + 3) $。
(2) 分解因式,得 $ (2x - 5)(2x + 1) = 0 $,
∴ $ 2x - 5 = 0 $ 或 $ 2x + 1 = 0 $,解得 $ x_1 = \frac{5}{2} $,$ x_2 = -\frac{1}{2} $。
(3) 分解因式,得 $ (3x - a)(x - 2) = 0 $,
∴ $ 3x - a = 0 $ 或 $ x - 2 = 0 $,解得 $ x_1 = \frac{a}{3} $,$ x_2 = 2 $。
查看更多完整答案,请扫码查看


