《2025年5年中考3年模拟九年级数学上册华师大版》

1. 「2024 甘肃兰州中考」如图,小张想估测被池塘隔开的 A,B 两处景观之间的距离,他先在 AB 外取一点 C,然后步测出 AC,BC 的中点 D,E,并步测出 DE 的长约为 18 m,由此估测 A,B 之间的距离为(36m)
A. 18 m
B. 24 m
C. 36 m
D. 54 m

答案： C
∵D,E分别是AC,BC的中点，
∴DE是△ABC的中位线，
∴AB = 2DE = 36m。

2. 「2024 四川广安中考」如图,在△ABC 中,点 D,E 分别是 AC,BC 的中点,若∠A = 45°,∠CED = 70°,则∠C 的度数为(65°)
A. 45°
B. 50°
C. 60°
D. 65°

答案： D
∵点D,E分别是AC,BC的中点，
∴DE是△ABC的中位线，
∴DE//AB，
∴∠B = ∠CED = 70°，
∴∠C = 180° - ∠A - ∠B = 180° - 45° - 70° = 65°。

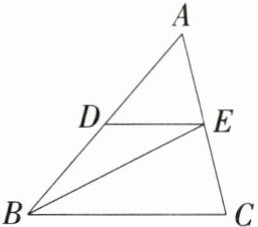
3. 「2024 浙江中考」如图,D,E 分别是△ABC 边 AB,AC 的中点,连结 BE,DE. 若∠AED = ∠BEC,DE = 2,则 BE 的长为______4.

答案： 答案 4
解析
∵D,E分别是△ABC边AB,AC的中点，
∴DE是△ABC的中位线，
∴BC = 2DE = 2×2 = 4，DE//BC，
∴∠AED = ∠C，
∵∠AED = ∠BEC，
∴∠BEC = ∠C，
∴BE = BC = 4。

4. 如图,在四边形 ABCD 中,E、F 分别是 AD、BC 的中点,G、H 分别是 BD、AC 的中点,AB = CD,EF 与 GH 有什么位置关系？请说明理由.

答案：
解析 EF⊥GH。理由：如图，连结GE、GF、HF、EH。
∵E、G分别是AD、BD的中点，
∴EG = $\frac{1}{2}$AB，同理HF = $\frac{1}{2}$AB，FG = $\frac{1}{2}$CD，EH = $\frac{1}{2}$CD，
∵AB = CD，
∴EG = GF = FH = EH，
∴四边形EGFH是菱形，
∴EF⊥GH。

5. 新考向 「2025 河南鹤壁淇县期中」下列选项中,用尺规作图所得点 P 是△ABC 的重心的是(C)

答案： C 三角形的重心是三条中线的交点，用尺规作图确定重心位置时，一般只需作出三角形的两条中线即可，其交点即为该三角形的重心。

6. 「2025 浙江宁波海曙兴宁中学月考」如图,△ABC 的重心为 G,△ABC 和△GBC 在 BC 边上的高之比为( )

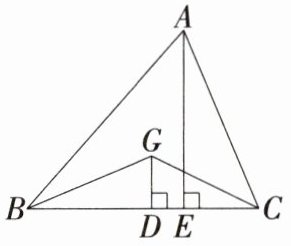
A. 1:2
B. 1:3
C. 2:1
D. 3:1

答案：
D 如图，连结AG，并延长交BC于F，
∵G是△ABC的重心，
∴AF = 3FG，
∵AE是△ABC的高，DG是△GBC的高，
∴DG//AE，
∴△FDG∽△FEA，
∴AE:DG = AF:FG = 3:1。

7. 「2025 山西晋城二模,」如图,已知点 M 是△ABC 的重心,AB = 18,MN//AB,则 MN 的长为(6)
A. 9
B. $\frac{9}{4}$
C. $\frac{9}{2}$
D. 6

答案： D
∵点M是△ABC的重心，
∴AD = DB = $\frac{1}{2}$AB = 9，$\frac{CM}{CD}$ = $\frac{2}{3}$，
∵MN//AB，
∴△CMN∽△CDB，
∴$\frac{MN}{DB}$ = $\frac{CM}{CD}$ = $\frac{2}{3}$，
∴$\frac{MN}{9}$ = $\frac{2}{3}$，解得MN = 6。

8. 教材变式 「2025 福建泉州永春二模,」如图,在△ABC 中,D,E,F 分别是边 AB,AC,BC 的中点,AF,CD,BE 相交于点 G,AF,BE,CD 分别与 DE,DF,EF 相交于点 H,M,N,若 AF = 18$\sqrt{5}$,则 GH 的长为(3$\sqrt{5}$)

A. 2$\sqrt{5}$
B. 3$\sqrt{5}$
C. $\sqrt{5}$
D. 6$\sqrt{5}$

答案： B
∵D,E,F分别是边AB,AC,BC的中点，
∴点G是△ABC的重心，
∴GF = $\frac{1}{3}$AF = $\frac{1}{3}$×18$\sqrt{5}$ = 6$\sqrt{5}$，EG = $\frac{1}{2}$GB，
∵D,E分别是边AB,AC的中点，
∴DE是△ABC的中位线，
∴DE//BC，
∴△EGH∽△BGF，
∴$\frac{GH}{GF}$ = $\frac{EG}{GB}$ = $\frac{1}{2}$，
∴GH = $\frac{1}{2}$GF = 3$\sqrt{5}$。