《2025年5年中考3年模拟九年级数学上册华师大版》

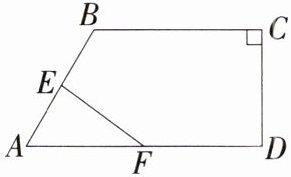
1.「2025四川资阳一模」如图,在四边形ABCD中,$∠C= 90^{\circ }$,E、F分别为AB、AD的中点,$BC= 2,CD= \frac {3}{2}$,则EF的长为____.

答案：
答案 $\frac{5}{4}$
解析 如图，连结 $BD$，在 $Rt\triangle BCD$ 中，$\angle C = 90^{\circ}$，$BC = 2$，$CD = \frac{3}{2}$，
$\therefore BD = \sqrt{BC^{2} + CD^{2}} = \frac{5}{2}$，$\because E$、$F$ 分别为 $AB$、$AD$ 的中点，$\therefore EF$ 是 $\triangle ABD$ 的中位线，
$\therefore EF = \frac{1}{2}BD = \frac{5}{4}$。

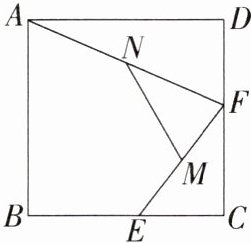
2.「2023广西中考」如图,在边长为2的正方形ABCD中,E,F分别是BC,CD上的动点,M,N分别是EF,AF的中点,则MN的最大值为$\sqrt{2}$.

答案： 答案 $\sqrt{2}$
解析 连结 $AE$（图略）。$\because M$，$N$ 分别是 $EF$，$AF$ 的中点，
$\therefore MN = \frac{1}{2}AE$。易知当点 $E$ 与点 $C$ 重合时，$AE$ 取得最大值，为 $2\sqrt{2}$，$\therefore MN$ 的最大值为 $\sqrt{2}$。

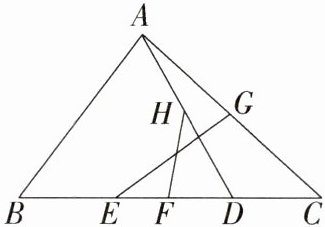
3.「2024福建漳州三中期中」已知:$△ABC$中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,求证:EG、HF互相平分.

答案：
证明 如图，连结 $EH$、$GH$、$GF$，$\because E$、$F$、$G$、$H$ 分别是 $BD$、$BC$、$AC$、$AD$ 的中点，$\therefore AB // EH // GF$，$GH // BC$，$\therefore$ 四边形 $EHGF$ 为平行四边形，$\therefore EG$、$HF$ 互相平分。

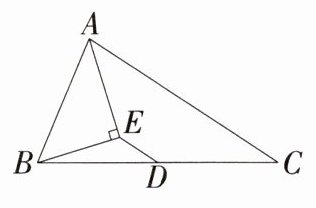
4.「2025湖南衡阳成章实验中学月考」如图,$△ABC$中,D是BC边的中点,AE平分$∠BAC,BE⊥AE$于E,若$AB= 5,AC= 7$,求ED的长.

答案：
解析 如图，延长 $BE$ 交 $AC$ 于 $F$，$\because AE$ 平分 $\angle BAC$，$BE \perp AE$，$\therefore \triangle BAF$ 是等腰三角形，
$\therefore BE = EF$，$AB = AF$，$\because AB = 5$，
$\therefore AF = 5$，
$\because AC = 7$，$\therefore CF = AC - AF = 7 - 5 = 2$，
$\because D$ 为 $BC$ 的中点，$\therefore DE$ 是 $\triangle BCF$ 的中位线，$\therefore DE = \frac{1}{2}CF = 1$。

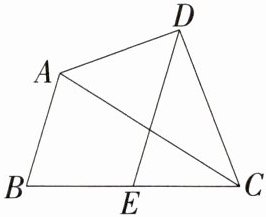
5.「2025河南洛阳孟津期中」如图,$△ABC$中,$AB= 8$,AD为$△ABC$的一个外角的平分线,且$AD⊥CD$于点D,E为BC的中点,若$DE= 10$,求AC的长.

答案：
解析 如图，延长 $BA$、$CD$ 交于点 $F$，
$\because AD$ 为 $\triangle ABC$ 的一个外角的平分线，$\therefore \angle DAF = \angle DAC$，
$\because AD \perp CD$，$\therefore \angle ADF = \angle ADC = 90^{\circ}$，
在 $\triangle ADF$ 和 $\triangle ADC$ 中，
$\left\{\begin{array}{l}\angle DAF = \angle DAC,\\AD = AD,\\\angle ADF = \angle ADC,\end{array}\right.$
$\therefore \triangle ADF \cong \triangle ADC$，$\therefore CD = DF$，$AC = AF$，
$\because E$ 为 $BC$ 的中点，$\therefore DE$ 是 $\triangle BCF$ 的中位线，
$\therefore BF = 2DE = 20$，
$\therefore AF = BF - AB = 20 - 8 = 12$，$\therefore AC = AF = 12$。