《2025年5年中考3年模拟九年级数学上册华师大版》

9. 「2025 湖南衡阳南岳一模,」如图,在△ABC 中,AB = AC,M、N 分别是 AB、AC 的中点,D、E 为 BC 上的点,连结 DN、EM,若 AB = 13 cm,BC = 10 cm,DE = 5 cm,则阴影部分的面积为( )

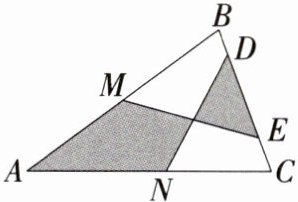
$A. 15 cm^2$
$B. 20 cm^2$
$C. 25 cm^2$
$D. 30 cm^2$

答案：
D 如图，连结MN，则MN是△ABC的中位线，
∴MN = $\frac{1}{2}$BC = 5cm，过点A作AF⊥BC于F，
∵AB = AC，
∴BF = CF = $\frac{1}{2}$BC = 5cm，由勾股定理得AF = $\sqrt{13^{2}-5^{2}}$ = 12(cm)。
∵图中阴影部分由三个底边长都是5cm，且高的和为12cm的三角形组成，
∴S阴影 = $\frac{1}{2}$×5×12 = 30(cm²)。

10. 「2024 吉林长春南关模拟,」【教材呈现】
如图所示的是九年级上册数学教材第 80 页的第 3 题,请完成这道题的证明.
 
证明：∵P,M,N分别是BD,DC,AB的中点，∴PM = $\frac{1}{2}$BC，PN = $\frac{1}{2}$AD，∵BC = AD，∴PM = PN，∴∠PMN = ∠PNM。
【结论应用】
(1)如图,在该题目的条件下,延长线段 AD 交 NM 的延长线于点 E,延长线段 BC 交 NM 的延长线于点 F,求证：∠AEN = ∠F.
证明：∵P,M,N分别是BD,DC,AB的中点，∴PM//BC，PN//AD，∴∠F = ∠PMN，∠AEN = ∠PNM，∵∠PMN = ∠PNM，∴∠AEN = ∠F。
(2)若(1)中的∠A + ∠ABC = 130°,求∠F 的大小.

解：∵∠A + ∠ANE + ∠AEN = 180°，∠NBF + ∠BNF + ∠F = 180°，∴∠A + ∠NBF + ∠ANE + ∠BNF + ∠AEN + ∠F = 360°，∴130° + 180° + 2∠F = 360°，∴∠F = 25°。

答案： 解析 【教材呈现】证明：
∵P,M,N分别是BD,DC,AB的中点，
∴PM = $\frac{1}{2}$BC，PN = $\frac{1}{2}$AD，
∵BC = AD，
∴PM = PN，
∴∠PMN = ∠PNM。
【结论应用】
(1) 证明：
∵P,M,N分别是BD,DC,AB的中点，
∴PM//BC，PN//AD，
∴∠F = ∠PMN，∠AEN = ∠PNM，
∵∠PMN = ∠PNM，
∴∠AEN = ∠F。
(2)
∵∠A + ∠ANE + ∠AEN = 180°，∠NBF + ∠BNF + ∠F = 180°，
∴∠A + ∠NBF + ∠ANE + ∠BNF + ∠AEN + ∠F = 360°，
∴130° + 180° + 2∠F = 360°，
∴∠F = 25°。

11. 新课标推理能力 定义：至少有一组对边相等的凸四边形为等对边四边形,如图,已知四边形 ABCD,点 E,F 是对角线 AC,BD 的中点,G 为 BC 的中点,连结 EF,FG,EG,△EFG 为等边三角形.
(1)求证：四边形 ABCD 是等对边四边形.
(2)若∠BAC + ∠BDC = 180°,求∠DBC 的度数.

答案：
解析
(1) 证明：
∵△EFG为等边三角形，
∴EG = FG，
∵点E,F是对角线AC,BD的中点，G为BC的中点，
∴EG是△CBA的中位线，FG是△BCD的中位线，
∴CD = 2FG，AB = 2EG，
∴CD = AB，
∴四边形ABCD是等对边四边形。
(2) 如图，过B作BM⊥CA交CA的延长线于M，过C作CN⊥BD于N，
∵∠BAC + ∠BDC = 180°，∠BAC + ∠BAM = 180°，
∴∠BAM = ∠CDN，
∵∠AMB = ∠DNC = 90°，AB = DC，
∴△BAM≌△CDN，
∴BM = CN，
∵BC = CB，
∴Rt△BCM≌Rt△CBN，
∴∠DBC = ∠ACB，
∵EG是△CBA的中位线，FG是△BCD的中位线，
∴EG//AB，FG//CD，
∴∠CEG = ∠BAC，∠BFG = ∠BDC，
∵∠BAC + ∠BDC = 180°，
∴∠CEG + ∠BFG = 180°，
∵△EFG是等边三角形，
∴∠EFG = ∠FEG = 60°，
∵∠BFG + ∠EFG + ∠EFD + ∠CEG + ∠FEG + ∠FEA = 180° + 180°，
∴∠EFD + ∠FEA = 60°，
∴∠DBC + ∠ACB = 60°，
∴∠DBC = $\frac{1}{2}$×60° = 30°。

 1. 平行四边形 ABCD 各边中点依次是 E,F,G,H,关于四边形 EFGH,下面结论一定成立的是( )

A. 有一个内角等于 90°
B. 有一组邻边相等
C. 对角线互相垂直
D. 对角线互相平分

答案：
D 如图，连结AC，
∵平行四边形ABCD各边中点依次是E,F,G,H，
∴EF是△ABC的中位线，GH是△ACD的中位线，
∴EF//AC，EF = $\frac{1}{2}$AC，GH//AC，GH = $\frac{1}{2}$AC，
∴EF//GH，EF = GH，
∴四边形EFGH是平行四边形，
∴对角线互相平分。

2. 「2025 甘肃天水九中月考」如图,在矩形 ABCD 中,顺次连结矩形四边的中点得到四边形 EFGH. 若 AB = 8,AD = 6,则四边形 EFGH 的周长等于

 ______.

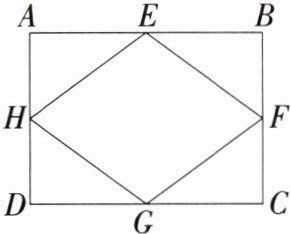
答案：
答案 20
解析 如图，连结AC、BD，在Rt△ABD中，BD = $\sqrt{AB^{2}+AD^{2}}$ = 10，
∵四边形ABCD是矩形，
∴AC = BD = 10，
∵E、H分别是AB、AD的中点，
∴EH = $\frac{1}{2}$BD = 5。同理可得，FG = $\frac{1}{2}$BD = 5，GH = $\frac{1}{2}$AC = 5，EF = $\frac{1}{2}$AC = 5，
∴四边形EFGH的周长 = 5×4 = 20。