第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
7.「2025河南周口沈丘一模,」如图1,有一张长32cm,宽16cm的长方形硬纸片,裁去角上2个小正方形和2个小长方形(图中阴影部分)之后,恰好能沿虚线折成如图2所示的有盖纸盒.若纸盒的底面积是$130cm^2,$则纸盒的高为______

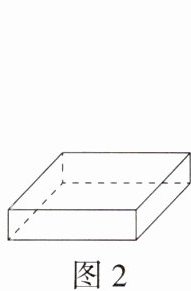
3
cm.

答案:
答案 3
解析 设纸盒的高为 $ x \, \text{cm} $,依题意得 $ \frac{32 - 2x}{2} \times (16 - 2x) = 130 $,整理得 $ x^2 - 24x + 63 = 0 $,解得 $ x_1 = 3 $,$ x_2 = 21 $。当 $ x = 3 $ 时,$ 16 - 2x = 10 > 0 $,符合题意;当 $ x = 21 $ 时,$ 16 - 2x = -26 < 0 $,不符合题意,舍去。故纸盒的高为 $ 3 \, \text{cm} $。
解析 设纸盒的高为 $ x \, \text{cm} $,依题意得 $ \frac{32 - 2x}{2} \times (16 - 2x) = 130 $,整理得 $ x^2 - 24x + 63 = 0 $,解得 $ x_1 = 3 $,$ x_2 = 21 $。当 $ x = 3 $ 时,$ 16 - 2x = 10 > 0 $,符合题意;当 $ x = 21 $ 时,$ 16 - 2x = -26 < 0 $,不符合题意,舍去。故纸盒的高为 $ 3 \, \text{cm} $。
8.新课标运算能力「2025重庆沙坪坝二模」如图,△ABC中,AC= 6√2cm,BC= 14cm,∠ACB= 45°,AD⊥BC于D.点P从点B出发,沿BD方向匀速运动,速度为2cm/s;同时,点Q从点D出发,沿DA方向匀速运动,速度为1cm/s.过点Q作QE⊥AD交AC于点E,连结PE.设运动时间为t s(0<t<4).解答下列问题:
(1)线段AD= ______cm,线段PD= ______cm(用含t的代数式表示).
(2)当四边形ABPE的面积为$119/4cm^2$时,求t的值.
(3)在运动过程中,是否存在某一时刻,使点Q在PE的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

(1)线段AD= ______cm,线段PD= ______cm(用含t的代数式表示).
(2)当四边形ABPE的面积为$119/4cm^2$时,求t的值.
(3)在运动过程中,是否存在某一时刻,使点Q在PE的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.

答案:
解析
(1)
∵ $ AD \perp BC $,
∴ $ \angle ADC = 90^\circ $,
∵ $ \angle C = 45^\circ $,
∴ $ AD = CD $,
∴ $ AD^2 + CD^2 = 2AD^2 = AC^2 = (6\sqrt{2})^2 $,
∴ $ AD = CD = 6 \, \text{cm} $,
∵ $ BC = 14 \, \text{cm} $,
∴ $ BD = BC - CD = 14 - 6 = 8 \, \text{cm} $,
∵ $ PB = 2t \, \text{cm} $,
∴ $ PD = (8 - 2t) \, \text{cm} $。故答案为 $ 6 $;$ (8 - 2t) $。
(2) 如图,过点 $ E $ 作 $ EH \perp BC $ 于点 $ H $,则四边形 $ DQEH $ 是矩形。
∵ $ \angle EHC = 90^\circ $,$ \angle C = 45^\circ $,
∴ $ EH = CH = QD = t \, \text{cm} $,
∵ $ S_{\text{四边形}ABPE} = S_{\triangle ABC} - S_{\triangle PCE} $,
∴ $ \frac{119}{4} = \frac{1}{2} \times 14 \times 6 - \frac{1}{2} \times (14 - 2t) \times t $,整理得 $ 4t^2 - 28t + 49 = 0 $,解得 $ t_1 = t_2 = \frac{7}{2} $。故当四边形 $ ABPE $ 的面积为 $ \frac{119}{4} \, \text{cm}^2 $ 时,$ t $ 的值为 $ \frac{7}{2} $。
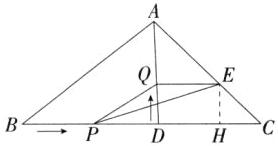
(3) 不存在。理由如下:若点 $ Q $ 在 $ PE $ 的垂直平分线上,则 $ QE = PQ $,易知 $ \triangle AQE $ 是等腰直角三角形,
∴ $ QE = AQ = (6 - t) \, \text{cm} $,在 $ \text{Rt} \triangle PQD $ 中,$ PD = (8 - 2t) \, \text{cm} $,$ QD = t \, \text{cm} $,由勾股定理得 $ PQ^2 = PD^2 + QD^2 = (8 - 2t)^2 + t^2 $,
∵ $ QE = PQ $,
∴ $ (6 - t)^2 = (8 - 2t)^2 + t^2 $,整理得 $ t^2 - 5t + 7 = 0 $,
∵ $ \Delta = (-5)^2 - 4 \times 1 \times 7 = -3 < 0 $,
∴ 方程无实数根,
∴ 不存在某一时刻,使点 $ Q $ 在 $ PE $ 的垂直平分线上。
解析
(1)
∵ $ AD \perp BC $,
∴ $ \angle ADC = 90^\circ $,
∵ $ \angle C = 45^\circ $,
∴ $ AD = CD $,
∴ $ AD^2 + CD^2 = 2AD^2 = AC^2 = (6\sqrt{2})^2 $,
∴ $ AD = CD = 6 \, \text{cm} $,
∵ $ BC = 14 \, \text{cm} $,
∴ $ BD = BC - CD = 14 - 6 = 8 \, \text{cm} $,
∵ $ PB = 2t \, \text{cm} $,
∴ $ PD = (8 - 2t) \, \text{cm} $。故答案为 $ 6 $;$ (8 - 2t) $。
(2) 如图,过点 $ E $ 作 $ EH \perp BC $ 于点 $ H $,则四边形 $ DQEH $ 是矩形。
∵ $ \angle EHC = 90^\circ $,$ \angle C = 45^\circ $,
∴ $ EH = CH = QD = t \, \text{cm} $,
∵ $ S_{\text{四边形}ABPE} = S_{\triangle ABC} - S_{\triangle PCE} $,
∴ $ \frac{119}{4} = \frac{1}{2} \times 14 \times 6 - \frac{1}{2} \times (14 - 2t) \times t $,整理得 $ 4t^2 - 28t + 49 = 0 $,解得 $ t_1 = t_2 = \frac{7}{2} $。故当四边形 $ ABPE $ 的面积为 $ \frac{119}{4} \, \text{cm}^2 $ 时,$ t $ 的值为 $ \frac{7}{2} $。

(3) 不存在。理由如下:若点 $ Q $ 在 $ PE $ 的垂直平分线上,则 $ QE = PQ $,易知 $ \triangle AQE $ 是等腰直角三角形,
∴ $ QE = AQ = (6 - t) \, \text{cm} $,在 $ \text{Rt} \triangle PQD $ 中,$ PD = (8 - 2t) \, \text{cm} $,$ QD = t \, \text{cm} $,由勾股定理得 $ PQ^2 = PD^2 + QD^2 = (8 - 2t)^2 + t^2 $,
∵ $ QE = PQ $,
∴ $ (6 - t)^2 = (8 - 2t)^2 + t^2 $,整理得 $ t^2 - 5t + 7 = 0 $,
∵ $ \Delta = (-5)^2 - 4 \times 1 \times 7 = -3 < 0 $,
∴ 方程无实数根,
∴ 不存在某一时刻,使点 $ Q $ 在 $ PE $ 的垂直平分线上。
例题 「2025重庆江津二中期中」如图,一块长12m,宽8m的长方形空地上,修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为$60m^2,$则道路的宽应为
2
m.
答案:
答案 2
解析 设道路的宽为 $ x \, \text{m} $,则剩余部分可合成长为 $ (12 - x) \, \text{m} $,宽为 $ (8 - x) \, \text{m} $ 的长方形,依题意得 $ (12 - x)(8 - x) = 60 $,整理得 $ x^2 - 20x + 36 = 0 $,解得 $ x_1 = 2 $,$ x_2 = 18 $(不合题意,舍去),
∴ 道路的宽为 $ 2 \, \text{m} $。
解析 设道路的宽为 $ x \, \text{m} $,则剩余部分可合成长为 $ (12 - x) \, \text{m} $,宽为 $ (8 - x) \, \text{m} $ 的长方形,依题意得 $ (12 - x)(8 - x) = 60 $,整理得 $ x^2 - 20x + 36 = 0 $,解得 $ x_1 = 2 $,$ x_2 = 18 $(不合题意,舍去),
∴ 道路的宽为 $ 2 \, \text{m} $。
1.如图所示,某市世纪广场有一块长18m,宽15m的长方形绿地,在绿地中开辟三条道路后剩余绿地的面积为$224m^2,$则图中x的值为(
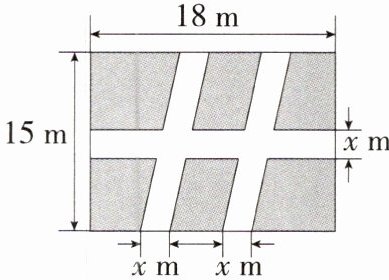
A.1
B.2
C.3
D.4
1
)
A.1
B.2
C.3
D.4
答案:
A 根据题意得剩余绿地可合成长为 $ (18 - 2x) \, \text{m} $,宽为 $ (15 - x) \, \text{m} $ 的长方形,则 $ (18 - 2x)(15 - x) = 224 $,整理得 $ x^2 - 24x + 23 = 0 $,解得 $ x_1 = 1 $,$ x_2 = 23 $(不符合题意,舍去),
∴ 题图中 $ x $ 的值为 1。
∴ 题图中 $ x $ 的值为 1。
2.「2025湖南衡阳成章实验中学月考」如图所示,某旅游景点要在一个长、宽分别为20m和12m的矩形水池ABCD中建一个与矩形的边互相平行的正方形观赏亭和连接观赏亭的四条道路,道路的宽度相等,其中两条与AB平行,另两条与BC平行,已知道路的宽为正方形观赏亭边长的1/4,若道路与观赏亭的面积之和是原矩形水池面积的1/6,则道路的宽为(
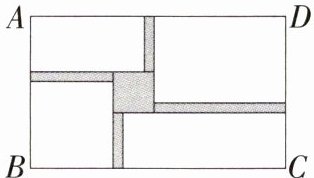
A.0.8m
B.1m
C.1.2m
D.0.8m或1.2m
1m
)
A.0.8m
B.1m
C.1.2m
D.0.8m或1.2m
答案:
B 设道路的宽为 $ x \, \text{m} $,则正方形的边长为 $ 4x \, \text{m} $,依题意得 $ x(12 - 4x) + x(20 - 4x) + 16x^2 = \frac{1}{6} \times 20 \times 12 $,整理得 $ x^2 + 4x - 5 = 0 $,解得 $ x_1 = 1 $,$ x_2 = -5 $(舍去),故道路的宽为 $ 1 \, \text{m} $。
查看更多完整答案,请扫码查看


