《2025年5年中考3年模拟九年级数学上册华师大版》

14.「2025吉林省第二实验学校一模改编,★☆」如果一个三角形的三边长分别为a,b,c,则该三角形的面积$S= \sqrt {\frac {1}{4}[a^{2}b^{2}-(\frac {a^{2}+b^{2}-c^{2}}{2})^{2}]}$。现已知$\triangle ABC的三边长分别为1,3,\sqrt {10}$,则$\triangle ABC$的面积为____$\frac{3}{2}$。

答案： 答案 $\frac{3}{2}$
解析 $\because \triangle ABC$ 的三边长分别为 $1$，$3$，$\sqrt{10}$，$\therefore S_{\triangle ABC} = \sqrt{\frac{1}{4}\times\left[1^{2}\times3^{2} - \left(\frac{1^{2} + 3^{2} - (\sqrt{10})^{2}}{2}\right)^{2}\right]} = \frac{3}{2}$。

15.「★☆」已知正实数a,b,c,d满足关系式$a+b+c+d= 1$,设$s= \sqrt {3a^{2}+1}+\sqrt {3b^{2}+1}+\sqrt {3c^{2}+1}+\sqrt {3d^{2}+1}$,那么s与5的大小关系为$s＜5$。

答案： 答案 $s＜5$
解析 $\because$ 正实数 $a$，$b$，$c$，$d$ 满足关系式 $a + b + c + d = 1$，$\therefore 0＜a＜1$，$a^{2}＜a$，$\therefore \sqrt{3a^{2} + 1}＜\sqrt{a^{2} + 2a + 1} = \sqrt{(a + 1)^{2}} = a + 1$，同理可得 $\sqrt{3b^{2} + 1}＜b + 1$，$\sqrt{3c^{2} + 1}＜c + 1$，$\sqrt{3d^{2} + 1}＜d + 1$。$\therefore s = \sqrt{3a^{2} + 1} + \sqrt{3b^{2} + 1} + \sqrt{3c^{2} + 1} + \sqrt{3d^{2} + 1}＜a + 1 + b + 1 + c + 1 + d + 1 = 5$，即 $s＜5$。

16.「2025山西晋城二模,★☆」求代数式$a+\sqrt {1-2a+a^{2}}$的值,其中$a= 1012$。下图是小亮和小芳的解答过程：

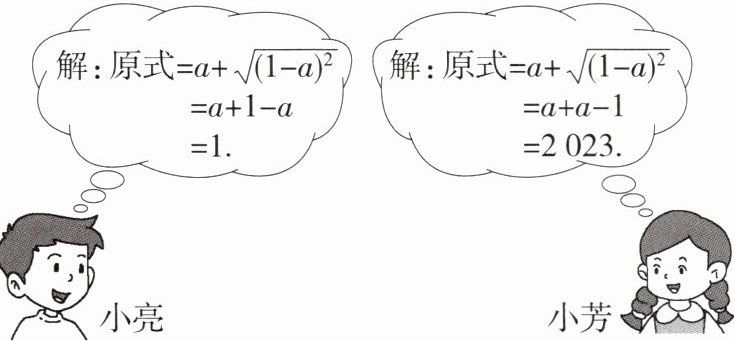
(1)小亮的解法是错误的。
(2)错误的原因在于未能正确地运用二次根式的性质：$\sqrt {a^{2}}=$$|a|$=$\begin{cases}a(a\geqslant0)\\-a(a＜0)\end{cases}$
(3)求代数式$a+2\sqrt {a^{2}-6a+9}$的值,其中$a= -2025$。2031

答案： 解析 （1）$\because a = 1012$，$\therefore 1 - a＜0$，$\therefore \sqrt{(1 - a)^{2}} = |1 - a| = a - 1$，$\therefore a + \sqrt{1 - 2a + a^{2}} = a + \sqrt{(1 - a)^{2}} = a + a - 1 = 2023$，$\therefore$ 小亮的解法是错误的。
（2）$|a|$；$\begin{cases}a(a\geqslant0)\\-a(a＜0)\end{cases}$。
（3）当 $a = - 2025$ 时，$a + 2\sqrt{a^{2} - 6a + 9} = a + 2\sqrt{(a - 3)^{2}} = a + 2|a - 3| = a + 2(3 - a) = - a + 6 = 2025 + 6 = 2031$。

17. 新课标运算能力「2024河南南阳唐河一模」阅读下列解题过程。
例：若代数式$\sqrt {(a-1)^{2}}+\sqrt {(a-3)^{2}}$的值是2,求a的取值范围。
解：$\sqrt {(a-1)^{2}}+\sqrt {(a-3)^{2}}= |a-1|+|a-3|$,
当$a＜1$时,原式$=(1-a)+(3-a)= 4-2a$,令$4-2a= 2$,解得$a= 1$(舍去)；
当$1≤a≤3$时,原式$=(a-1)+(3-a)= 2$,符合条件；
当$a＞3$时,原式$=(a-1)+(a-3)= 2a-4$,令$2a-4= 2$,解得$a= 3$(舍去)。
综上所述,a的取值范围是$1≤a≤3$。
上述解题过程主要运用了分类讨论的方法,请你根据上述解法,解答问题。
(1)当$2≤a≤5$时,化简：$\sqrt {(a-2)^{2}}+\sqrt {(a-5)^{2}}=$3。
(2)若等式$\sqrt {(3-a)^{2}}+\sqrt {(a-7)^{2}}= 4$成立,则a的取值范围是$3\leqslant a\leqslant7$。
(3)若$\sqrt {(a+1)^{2}}+\sqrt {(a-5)^{2}}= 8$,求a的取值。
$a = - 2$ 或 $a = 6$

答案： 解析 （1）$\because 2\leqslant a\leqslant5$，$\therefore a - 2\geqslant0$，$a - 5\leqslant0$，$\therefore$ 原式 $= |a - 2| + |a - 5| = a - 2 - (a - 5) = 3$。
（2）$\sqrt{(3 - a)^{2}} + \sqrt{(a - 7)^{2}} = |3 - a| + |a - 7| = 4$，当 $a\leqslant3$ 时，$3 - a\geqslant0$，$a - 7＜0$，$\therefore |3 - a| + |a - 7| = 3 - a - (a - 7) = 4$，$\therefore a = 3$，符合题意；当 $3＜a＜7$ 时，$3 - a＜0$，$a - 7＜0$，$\therefore |3 - a| + |a - 7| = - (3 - a) - (a - 7) = 4$，符合题意；当 $a\geqslant7$ 时，$3 - a＜0$，$a - 7\geqslant0$，$\therefore |3 - a| + |a - 7| = - (3 - a) + (a - 7) = 4$，$\therefore a = 7$，符合题意。综上所述，$a$ 的取值范围是 $3\leqslant a\leqslant7$。
（3）$\sqrt{(a + 1)^{2}} + \sqrt{(a - 5)^{2}} = |a + 1| + |a - 5| = 8$，当 $a\leqslant - 1$ 时，$a + 1\leqslant0$，$a - 5＜0$，$\therefore |a + 1| + |a - 5| = - (a + 1) - (a - 5) = 8$，解得 $a = - 2$，符合题意；当 $- 1＜a＜5$ 时，$a + 1＞0$，$a - 5＜0$，$\therefore |a + 1| + |a - 5| = a + 1 - (a - 5) = 8$，此方程无解，舍去；当 $a\geqslant5$ 时，$a + 1＞0$，$a - 5\geqslant0$，$\therefore |a + 1| + |a - 5| = a + 1 + a - 5 = 8$，解得 $a = 6$，符合题意。综上所述，$a = - 2$ 或 $a = 6$。

1. 若$y= \sqrt {4-x}+\sqrt {x-4}+2$,则$x^{y}$的值为(B)
A. 8
B. 16
C. -8
D. -16

答案： B 由题意得 $4 - x\geqslant0$，$x - 4\geqslant0$，解得 $x = 4$，则 $y = 2$，$\therefore x^{y} = 4^{2} = 16$。

2. 已知$a^{2}+\sqrt {2b-12}= 12a-36$,则$\sqrt {ab}$的值为____6。

答案： 答案 6
解析 $\because a^{2} + \sqrt{2b - 12} = 12a - 36$，$\therefore a^{2} - 12a + 36 + \sqrt{2b - 12} = 0$，即 $(a - 6)^{2} + \sqrt{2b - 12} = 0$，$\therefore a - 6 = 0$，$2b - 12 = 0$，$\therefore a = 6$，$b = 6$，$\therefore ab = 36$，$\therefore \sqrt{ab} = 6$。

3. 已知$|m-\sqrt {2}|+\sqrt {n-2}+(p-\sqrt {2})^{2}= 0$,则以m,n,p为三边长的三角形是等腰直角三角形。

答案： 答案 等腰直角
解析 依题意可得 $m - \sqrt{2} = 0$，$n - 2 = 0$，$p - \sqrt{2} = 0$，解得 $m = \sqrt{2}$，$n = 2$，$p = \sqrt{2}$，$\therefore m = p$。$\because (\sqrt{2})^{2} + (\sqrt{2})^{2} = 4 = 2^{2}$，即 $m^{2} + p^{2} = n^{2}$，$\therefore$ 以 $m$，$n$，$p$ 为三边长的三角形是等腰直角三角形。