《2025年海淀单元测试AB卷六年级数学下册鲁教版》

23. [10分/12分] 新考向 开放题 如图是李老师在课堂上展示的一道数学题，小颖的解题过程如下：
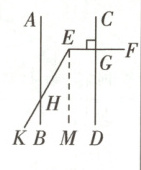
如图，$AB// CD$，$EF\perp CD$于点$G$，$EK$交$AB$于点$H$，当$\angle BHK = 30^{\circ}$时，求$\angle KEF$的度数。
解：如图，过点$E$作$EM// AB$。
因为$EM// AB$，$\angle BHK = 30^{\circ}$，
所以$\angle MEK=\angle BHK = 30^{\circ}$，
……
（1）请你补全小颖的解题过程。
（2）李老师还提供了两种解题思路。思路一：过点$H$作$HN// EF$交$CD$于点$N$。思路二：过点$G$作$GQ// EK$交$AB$于点$O$。请你从中任选一种，写出解题过程。

答案：
解:
(1)如题图,过点E作$EM// AB$.因为$EM// AB,∠BHK = 30^{\circ}$,所以$∠MEK = ∠BHK = 30^{\circ}$.因为$EF⊥CD$,所以$∠EGC = 90^{\circ}$.因为$AB// CD$,所以$EM// CD$,所以$∠MEG = ∠EGC = 90^{\circ}$,所以$∠KEF = ∠MEK + ∠MEG = 120^{\circ}$.
(2)选择思路一:如图①,过点H作$HN// EF$交CD于点N.因为$HN// EF,EF⊥CD$,所以$∠GNH = ∠CGE = 90^{\circ},∠KEF = ∠KHN$.因为$AB// CD$,所以$∠BHN = ∠GNH = 90^{\circ}$.因为$∠BHK = 30^{\circ}$,所以$∠KHN = ∠KHB + ∠BHN = 120^{\circ}$,所以$∠KEF = 120^{\circ}$.选择思路二:如图②,过点G作$GQ// EK$交AB于点O.因为$GO// EK,∠BHK = 30^{\circ}$,所以$∠QOB = ∠BHK = 30^{\circ},∠KEF + ∠EGO = 180^{\circ}$.因为$AB// CD$,所以$∠OGD = ∠QOB = 30^{\circ}$.因为$EF⊥CD$,所以$∠EGD = 90^{\circ}$,所以$∠EGO = ∠EGD - ∠OGD = 60^{\circ}$,所以$∠KEF = 180^{\circ}-∠EGO = 120^{\circ}$(任选其中一种作答即可)
　

24. [12分/14分] （威海文登期中）两个边长分别为$a$和$b$的正方形如图放置（图①），其未叠合部分（阴影）的面积为$S_{1}$；若再在图①中大正方形的右下角摆放一个边长为$b$的小正方形（如图②），两个小正方形叠合部分（阴影）的面积为$S_{2}$。
（1）用含$a$，$b$的代数式分别表示$S_{1}$，$S_{2}$。
（2）若$a + b = 10$，$ab = 23$，求$S_{1}+S_{2}$的值。
（3）当$S_{1}+S_{2}=28$时，求出图③中阴影部分的面积$S_{3}$。

答案： 解:
(1)由题图①②,可得$S_{1}=a^{2}-b^{2},S_{2}=2b^{2}-ab$.
(2)因为$a + b = 10,ab = 23$,所以$S_{1}+S_{2}=a^{2}-b^{2}+2b^{2}-ab=a^{2}+b^{2}-ab=(a + b)^{2}-3ab=100 - 3×23 = 31$,所以$S_{1}+S_{2}$的值为31.
(3)由题图③,得$S_{3}=a^{2}+b^{2}-\frac{1}{2}b(a + b)-\frac{1}{2}a^{2}=\frac{1}{2}(a^{2}+b^{2}-ab)$.因为$S_{1}+S_{2}=a^{2}+b^{2}-ab = 28$,所以$S_{3}=\frac{1}{2}×28 = 14$,所以题图③中阴影部分的面积$S_{3}$为14.