2025年海淀单元测试AB卷六年级数学下册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年海淀单元测试AB卷六年级数学下册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第53页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
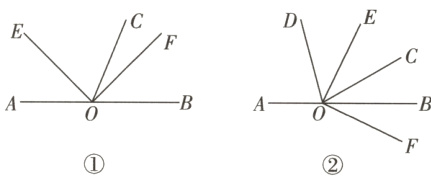
21. [8分/10分] (济南莱芜期末)已知O为直线AB上一点,∠EOF为直角,OC平分∠BOE.
(1)如图①,若∠AOE = 45°,求∠COF的度数.
(2)若∠EOF的位置如图②所示,OD平分∠AOC,且∠AOD = 75°,求∠COF的度数.
(1)如图①,若∠AOE = 45°,求∠COF的度数.
(2)若∠EOF的位置如图②所示,OD平分∠AOC,且∠AOD = 75°,求∠COF的度数.

答案:
解:
(1)因为∠AOE = 45°,所以∠BOE = 135°.因为OC平分∠BOE,所以∠COE = 67.5°.因为∠EOF为直角,所以∠COF = ∠EOF - ∠EOC = 22.5°.
(2)因为OD平分∠AOC,所以∠AOC = 2∠AOD = 2×75° = 150°,所以∠BOC = 180° - ∠AOC = 30°.因为OC平分∠BOE,所以∠EOC = ∠BOC = 30°,所以∠COF = ∠EOF - ∠EOC = 90° - 30° = 60°.
(1)因为∠AOE = 45°,所以∠BOE = 135°.因为OC平分∠BOE,所以∠COE = 67.5°.因为∠EOF为直角,所以∠COF = ∠EOF - ∠EOC = 22.5°.
(2)因为OD平分∠AOC,所以∠AOC = 2∠AOD = 2×75° = 150°,所以∠BOC = 180° - ∠AOC = 30°.因为OC平分∠BOE,所以∠EOC = ∠BOC = 30°,所以∠COF = ∠EOF - ∠EOC = 90° - 30° = 60°.
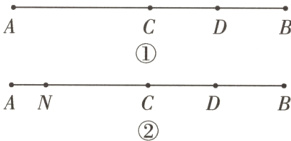
22. [10分/12分] (济宁任城期中)如图,线段AB = 16,点C是线段AB的中点,点D是线段BC的中点.
(1)如图①,求线段AD的长.
(2)如图②,点N是线段AC上一点,且NC = 3AN,求DN的长.
(3)在(2)的条件下,点M是线段AB上一点,且MC = 2,求MN的长.
(1)如图①,求线段AD的长.
(2)如图②,点N是线段AC上一点,且NC = 3AN,求DN的长.
(3)在(2)的条件下,点M是线段AB上一点,且MC = 2,求MN的长.

答案:
解:
(1)
∵点C是线段AB的中点,点D是线段BC的中点,
∴BC = AC = $\frac{1}{2}$AB,BD = $\frac{1}{2}$BC,
∴BD = $\frac{1}{4}$AB.
∵AB = 16,AD = AB - BD,
∴AD = 12.
(2)
∵NC = 3AN,
∴设AN = x,则NC = 3x.
∵AC = $\frac{1}{2}$AB = 8,
∴x + 3x = 8,解得x = 2,
∴AN = 2,NC = 6.
∵DN = AD - AN,
∴DN = 10.
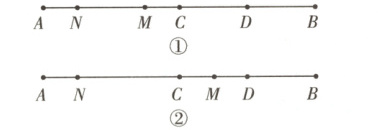
(3)当点M在点C左边时,如图①.
∵NC = 6,MC = 2,
∴MN = NC - MC = 4.当点M在点C右边时,如图②.
∵NC = 6,MC = 2,
∴MN = NC + MC = 8.
解:
(1)
∵点C是线段AB的中点,点D是线段BC的中点,
∴BC = AC = $\frac{1}{2}$AB,BD = $\frac{1}{2}$BC,
∴BD = $\frac{1}{4}$AB.
∵AB = 16,AD = AB - BD,
∴AD = 12.
(2)
∵NC = 3AN,
∴设AN = x,则NC = 3x.
∵AC = $\frac{1}{2}$AB = 8,
∴x + 3x = 8,解得x = 2,
∴AN = 2,NC = 6.
∵DN = AD - AN,
∴DN = 10.
(3)当点M在点C左边时,如图①.
∵NC = 6,MC = 2,
∴MN = NC - MC = 4.当点M在点C右边时,如图②.
∵NC = 6,MC = 2,
∴MN = NC + MC = 8.

23. [12分/14分] 【新课标 模型观念】(烟台牟平期末)某超市第一次用7 000元购进A,B两种商品,其中B商品的件数比A商品件数的$\frac{1}{2}$多20件,A,B两种商品的进价和售价如下表.
|商品|A|B|
|----|----|----|
|进价/(元/件)|25|30|
|售价/(元/件)|35|40|
(1)求该超市第一次购进A,B两种商品各多少件.
(2)该超市将第一次购进的A,B两种商品全部卖完后一共可获得多少利润?A商品的利润率是多少?
(3)该超市第二次以第一次的进价又购进A,B两种商品. 其中A商品的件数不变,B商品的件数是第一次的2倍;A商品按原售价销售,B商品按原售价打折销售. 第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多200元,求第二次B商品是按原价打几折销售.
|商品|A|B|
|----|----|----|
|进价/(元/件)|25|30|
|售价/(元/件)|35|40|
(1)求该超市第一次购进A,B两种商品各多少件.
(2)该超市将第一次购进的A,B两种商品全部卖完后一共可获得多少利润?A商品的利润率是多少?
(3)该超市第二次以第一次的进价又购进A,B两种商品. 其中A商品的件数不变,B商品的件数是第一次的2倍;A商品按原售价销售,B商品按原售价打折销售. 第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多200元,求第二次B商品是按原价打几折销售.
答案:
解:
(1)设第一次购进A商品x件,则购进B商品($\frac{1}{2}$x + 20)件.由题意,得25x + 30×($\frac{1}{2}$x + 20)=7000,解得x = 160,则$\frac{1}{2}$x + 20 = 80 + 20 = 100,因此,该超市第一次购进A商品160件,B商品100件.
(2)(35 - 25)×160+(40 - 30)×100 = 2600(元),因此,两种商品全部卖完后可获得2600元利润.$\frac{35 - 25}{25}$×100% = 40%,因此,A商品的利润率是40%.
(3)设第二次B商品是按原价打y折销售.由题意得,(35 - 25)×160+(40×$\frac{y}{10}$ - 30)×100×2 = 2600 + 200,解得y = 9.因此,第二次B商品是按原价打九折销售.
(1)设第一次购进A商品x件,则购进B商品($\frac{1}{2}$x + 20)件.由题意,得25x + 30×($\frac{1}{2}$x + 20)=7000,解得x = 160,则$\frac{1}{2}$x + 20 = 80 + 20 = 100,因此,该超市第一次购进A商品160件,B商品100件.
(2)(35 - 25)×160+(40 - 30)×100 = 2600(元),因此,两种商品全部卖完后可获得2600元利润.$\frac{35 - 25}{25}$×100% = 40%,因此,A商品的利润率是40%.
(3)设第二次B商品是按原价打y折销售.由题意得,(35 - 25)×160+(40×$\frac{y}{10}$ - 30)×100×2 = 2600 + 200,解得y = 9.因此,第二次B商品是按原价打九折销售.
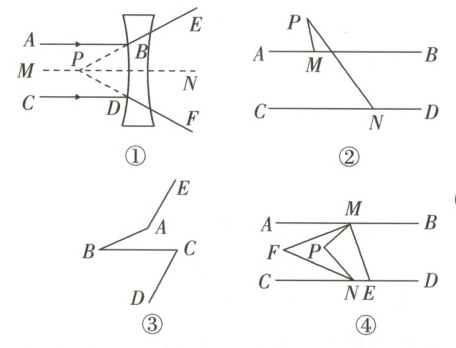
24. [12分/14分] 【新考向 探究题】【发现问题】如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
【提出问题】小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 _______;如图③,已知∠ABC = 25°,∠C = 60°,AE//CD,则∠BAE = _______ °.(不需要写解答过程)
探究三:如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P = 2∠F,求∠FME的度数.
【提出问题】小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 _______;如图③,已知∠ABC = 25°,∠C = 60°,AE//CD,则∠BAE = _______ °.(不需要写解答过程)
探究三:如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P = 2∠F,求∠FME的度数.

答案:
解:探究一:∠BPD = ∠ABP + ∠CDP.理由如下:
∵AB//MN//CD,
∴∠BPN = ∠ABP,∠DPN = ∠CDP,
∴∠BPN + ∠DPN = ∠ABP + ∠CDP,
∴∠BPD = ∠ABP + ∠CDP.
探究二:∠AMP = ∠P + ∠CNP 145
探究三:
∵射线ME,NF分别平分∠BMP和∠CNP,
∴∠PME = $\frac{1}{2}$∠PMB,∠CNF = ∠PNF.由探究一的结论,得∠P = ∠AMF + ∠PMF + ∠CNF + ∠PNF,∠F = ∠AMF + ∠CNF.
∵∠P = 2∠F,
∴∠AMF + ∠PMF + ∠CNF + ∠PNF = 2∠AMF + 2∠CNF.
∵∠CNF = ∠PNF,
∴∠AMF + ∠PMF = 2∠AMF,
∴∠PMF = ∠AMF = $\frac{1}{2}$∠AMP,
∴∠PMF + ∠PME = $\frac{1}{2}$(∠AMP + ∠PMB),
∴∠FME = $\frac{1}{2}$∠AMB = $\frac{1}{2}$×180° = 90°.
∵AB//MN//CD,
∴∠BPN = ∠ABP,∠DPN = ∠CDP,
∴∠BPN + ∠DPN = ∠ABP + ∠CDP,
∴∠BPD = ∠ABP + ∠CDP.
探究二:∠AMP = ∠P + ∠CNP 145
探究三:
∵射线ME,NF分别平分∠BMP和∠CNP,
∴∠PME = $\frac{1}{2}$∠PMB,∠CNF = ∠PNF.由探究一的结论,得∠P = ∠AMF + ∠PMF + ∠CNF + ∠PNF,∠F = ∠AMF + ∠CNF.
∵∠P = 2∠F,
∴∠AMF + ∠PMF + ∠CNF + ∠PNF = 2∠AMF + 2∠CNF.
∵∠CNF = ∠PNF,
∴∠AMF + ∠PMF = 2∠AMF,
∴∠PMF = ∠AMF = $\frac{1}{2}$∠AMP,
∴∠PMF + ∠PME = $\frac{1}{2}$(∠AMP + ∠PMB),
∴∠FME = $\frac{1}{2}$∠AMB = $\frac{1}{2}$×180° = 90°.
查看更多完整答案,请扫码查看


