《2025年海淀单元测试AB卷六年级数学下册鲁教版》

23.(12分 14分 新考向 探究题)已知：∠AOB和∠COD都是直角.
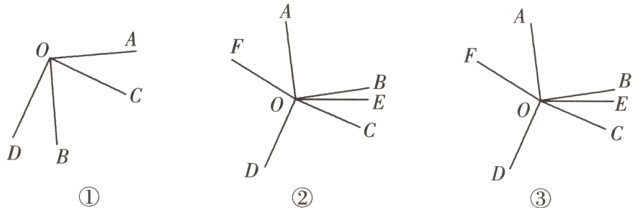
(1)如图①，当射线OB在∠COD内部时，请探究∠AOD和∠BOC之间的关系.
(2)如图②，当射线OA、射线OB都在∠COD的外部时，过点O作射线OE、射线OF，满足∠BOE = $\frac{1}{3}$∠BOC，∠DOF = $\frac{2}{3}$∠AOD，求∠EOF的度数.
(3)如图③，在(2)的条件下，在平面内是否存在射线OG，使得∠GOF∶∠GOE = 2∶3？若存在，求出∠GOF的度数；若不存在，请说明理由.

答案： 解:
(1)因为∠AOB和∠COD都是直角，所以∠AOB = ∠COD = 90°.因为∠BOD + ∠BOC = ∠COD,所以∠BOD = 90° - ∠BOC,所以∠AOD = ∠AOB + ∠BOD = 90° + 90° - ∠BOC = 180° - ∠BOC,所以∠AOD + ∠BOC = 180°.
(2)设∠BOE = α,则∠BOC = 3α.因为∠BOE + ∠EOC = ∠BOC,所以∠EOC = ∠BOC - ∠BOE = 2α.因为∠AOD + ∠COD + ∠BOC + ∠AOB = 360°,所以∠AOD = 360° - ∠COD - ∠BOC - ∠AOB = 360° - 90° - 3α - 90° = 180° - 3α.因为∠DOF = $\frac{2}{3}$∠AOD,所以∠DOF = $\frac{2}{3}$(180° - 3α)=120° - 2α,所以∠AOF = $\frac{1}{3}$∠AOD = $\frac{1}{3}$(180° - 3α)=60° - α,所以∠EOF = ∠BOE + ∠AOB + ∠AOF = α + 90° + 60° - α = 150°,所以∠EOF的度数为150°.
(3)存在.①当射线OG在∠EOF内部时，因为∠GOF∶∠GOE = 2∶3,所以∠GOF = $\frac{2}{2 + 3}$(∠GOF + ∠GOE)= $\frac{2}{5}$∠EOF = $\frac{2}{5}$×150° = 60°;②当射线OG在∠EOF外部时，因为∠GOF∶∠GOE = 2∶3,所以∠GOF = $\frac{2}{2 + 3}$(∠GOF + ∠GOE)= $\frac{2}{5}$(∠DOF + ∠COD + ∠EOC)= $\frac{2}{5}$×(120° - 2α + 90° + 2α)=84°.综上所述，∠GOF的度数是60°或84°.

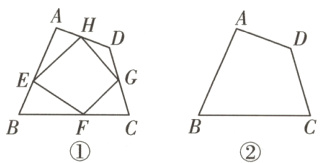
24.(12分 14分 新教材 变式题)(1)如图①，在四边形ABCD的各边上任意取一个点，分别是E，F，G，H，并顺次连接得到四边形EFGH，则四边形EFGH的周长一定小于原四边形ABCD的周长，请根据线段的性质说明理由.
∵EF ＜ BE + BF，(________________)
同理可得FG ＜ CF + CG，
HG ＜ DH + DG，
EH ＜ AE + AH，
∴EF + FG + HG + EH ＜ AB + BC + CD + DA.
即四边形EFGH的周长小于四边形ABCD的周长.
(2)联系拓广：
在四边形ABCD内一定存在一点P，使点P到四个顶点的距离之和最短.
请在图②中画出这个点，并说明理由.(提示：要想说明点P到四个顶点的距离之和最短，只需在该四边形内部另找任意的一个点Q，说明点Q到四个顶点的距离之和大于点P到四个顶点的距离之和即可)

答案：
解:
(1)两点之间线段最短
(2)如图，连接AC,BD,其交点为P,点P即为所求.理由如下:在四边形ABCD的内部任取一点Q,连接QA,QB,QC,QD.
∵BD ＜ QB + QD,AC ＜ QC + QA,
∴AC + BD ＜ QA + QB + QC + QD,
∴PA + PB + PC + PD ＜ QA + QB + QC + QD.即点P是四边形ABCD内到四个顶点距离之和最短的点.