《2025年海淀单元测试AB卷六年级数学下册鲁教版》

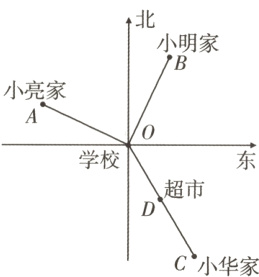
22. [10分 12分] 新教材 变式题 如图，点A，B，C，D，O分别表示小亮家、小明家、小华家、超市、学校的位置，点A位于点O北偏西65°，点B位于点O北偏东25°，点C位于点O南偏东30°，且点D是线段OC的中点。
(1)计算∠AOB，∠COB的度数。
(2)小亮与小华均以80米/分的速度从家出发去上学，到学校的时间分别是10分钟、15分钟。 若小亮沿“家→学校→超市”的路线买文具，请你计算他家到超市的路程。

答案： 解：
(1)∠AOB = 65° + 25° = 90°，∠COB = 180° - 25° - 30° = 125°.
(2)小亮家到学校的路程是 AO = 80×10 = 800(米)，小华家到学校的路程是 CO = 80×15 = 1200(米). 因为点 D 是线段 OC 的中点，所以 OD = $\frac{1}{2}$OC = $\frac{1}{2}$×1200 = 600(米)，则小亮家到超市的路程是 AO + OD = 800 + 600 = 1400(米).

23. [10分 12分] 辨思维 设元法 已知C，D两点将线段AB分为三部分，且AC∶CD∶DB = 2∶3∶4，若AB的中点为点M，BD的中点为点N，且MN = 5，求AB的长。

答案：
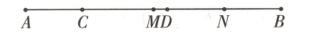
解：如图，因为 C，D 两点将线段 AB 分为三部分，且 AC：CD：DB = 2：3：4，设 AC = 2x，则 CD = 3x，DB = 4x，所以 AB = AC + CD + DB = 2x + 3x + 4x = 9x. 因为 AB 的中点为点 M，BD 的中点为点 N，所以 BM = $\frac{1}{2}$AB = $\frac{9}{2}$x，BN = $\frac{1}{2}$BD = 2x，所以 MN = BM - BN = $\frac{9}{2}$x - 2x = 5，解得 x = 2，所以 AB = 9x = 9×2 = 18.

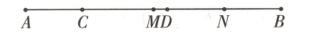
24. [13分 14分] 新考向 探究题 (淄博张店月考)将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕。
(1)如图①，求∠CBD的度数。
(2)如图②，若∠A′BE′ = 50°，求∠CBD的度数。
(3)如图③，若∠A′BE′ = α，请写出∠CBD的度数。(用含α的式子表示)

答案： 解：
(1)由题意知∠ABC = ∠A'BC，∠EBD = ∠E'BD，
∴∠A'BC = $\frac{1}{2}$∠ABA'，∠E'BD = $\frac{1}{2}$∠E'BE，
∴∠CBD = $\frac{1}{2}$(∠ABA' + ∠E'BE) = 90°.
(2)
∵∠A'BE' = 50°，
∴∠ABA' + ∠EBE' = 180° - ∠A'BE' = 130°.
∵∠A'BC = $\frac{1}{2}$∠ABA'，∠DBE' = $\frac{1}{2}$∠EBE'，
∴∠CBA' + ∠DBE' = $\frac{1}{2}$(∠ABA' + ∠EBE') = 65°，
∴∠CBD = ∠CBA' + ∠DBE' + ∠A'BE' = 65° + 50° = 115°.
(3)
∵∠A'BC = $\frac{1}{2}$∠ABA'，∠DBE' = $\frac{1}{2}$∠EBE'，
∴∠CBA' + ∠DBE' = $\frac{1}{2}$(∠ABA' + ∠EBE')，
∴∠CBD = ∠CBA' + ∠DBE' - ∠A'BE' = $\frac{1}{2}$(∠ABA' + ∠EBE') - ∠A'BE' = $\frac{1}{2}$(180° + α) - α = 90° - $\frac{α}{2}$.