《2025年海淀单元测试AB卷六年级数学下册鲁教版》

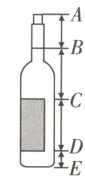
19. (8分 8分)(淄博桓台期中)如图是一种盛装葡萄酒的瓶子，已量得瓶塞$AB$与标签$CD$的高度之比为2∶3，且标签底部$DE=\frac{1}{2}AB$，$C$是$BD$的中点，又量得$AE = 330$ mm，求标签$CD$的高度.

答案： 解：设DE的长为x mm。由DE = $\frac{1}{2}$AB，得AB = 2DE = 2x mm。由AB:CD = 2:3，AB = 2x mm，得CD = 3x mm。$\because$C是BD的中点，$\therefore$BC = CD = 3x mm。$\because$AE = 330 mm，$\therefore$AB + BC + CD + DE = 2x + 3x + 3x + x = 330，$\therefore$x = $\frac{110}{3}$，3x = 110，$\therefore$标签CD的高度为110 mm。

20. (8分 10分)(烟台栖霞期末)小聪在做解方程练习时，其中有一个方程“$2y-\frac{1}{2}=\frac{1}{2}y+\blacksquare$”中的$\blacksquare$没印清晰，小聪问老师，老师说：“$\blacksquare$是一个有理数，该方程的解与当$x = 2$时代数式$5(x - 1)-2(x - 2)-4$的值相同.”小聪很快补上了这个常数. 同学们，你们能补上这个常数吗？请试一试.

答案：
解：当x = 2时，代数式5(x - 1)-2(x - 2)-4 = 5x - 5 - 2x + 4 - 4 = 3x - 5 = 3×2 - 5 = 1，即y = 1，代入方程中得到2×1 - $\frac{1}{2}$ = $\frac{1}{2}$×1 + ，解得 = 1。即这个常数是1。

21. [10分 12分](淄博张店月考)如图所示的一个圆分割成四个扇形，它们的圆心角的度数比为2∶3∶4∶3.
(1)求这四个扇形的圆心角的度数，并画出四个扇形.
(2)若圆的半径为2 cm，请分别求出这四个扇形的面积.

答案：
解：
(1)如图所示，$\because$一个圆分割成四个扇形，它们的圆心角的度数比为2:3:4:3，$\therefore$它们所对的圆心角分别为360°×$\frac{2}{12}$ = 60°，360°×$\frac{3}{12}$ = 90°，360°×$\frac{4}{12}$ = 120°，360°×$\frac{3}{12}$ = 90°。 已知圆的半径为2 cm，$\therefore$S1 = $\frac{60π×2²}{360}$ = $\frac{2}{3}$π(cm²)，S2 = $\frac{120π×2²}{360}$ = $\frac{4}{3}$π(cm²)，S3 = $\frac{90π×2²}{360}$ = π(cm²)，S4 = $\frac{90π×2²}{360}$ = π(cm²)。