2025年海淀单元测试AB卷六年级数学下册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年海淀单元测试AB卷六年级数学下册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
6. 【新课标 抽象能力】(烟台招远期末)如图,追梦小组在编写数学谜题时, 内要求填写同一个数字,若设 内的数字为t,则列出的方程正确的是( )
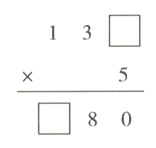
A. $13t×5=t + 80$
B. $5(130 + t)=100t + 80$
C. $5(130 + t)=80t$
D. $13 + t=100t + 80$
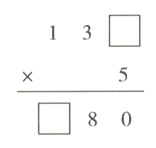
A. $13t×5=t + 80$
B. $5(130 + t)=100t + 80$
C. $5(130 + t)=80t$
D. $13 + t=100t + 80$
答案:
B
7. (泰安泰山期中)下列说法中,正确的是( )
A. 一个角的补角一定大于这个角
B. 任何一个角都有补角
C. 若∠1 + ∠2 + ∠3 = 90°,则∠1,∠2,∠3互余
D. 一个角若有余角,则这个角的补角与它的余角的差为90°
A. 一个角的补角一定大于这个角
B. 任何一个角都有补角
C. 若∠1 + ∠2 + ∠3 = 90°,则∠1,∠2,∠3互余
D. 一个角若有余角,则这个角的补角与它的余角的差为90°
答案:
D
8. (烟台蓬莱期中)六年级正在举办“线段争霸赛”,题板上出示一个抢答题目:如图,点C为线段AB上一点,AC - BC = 4,点M为线段AC中点,AM = 6,点N为线段MB的中点,则CN =( )
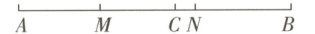
A. 2
B. 1
C. 1.5
D. 3
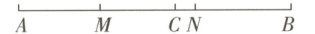
A. 2
B. 1
C. 1.5
D. 3
答案:
B [解析]
∵点M为AC的中点,
∴MC = AM = 6,
∴AC = 12.
∵AC - BC = 4,
∴BC = 8,
∴MB = MC + BC = 6 + 8 = 14.又
∵点N为BM的中点,
∴MN = $\frac{1}{2}$BM = $\frac{1}{2}$×14 = 7,
∴CN = MN - MC = 7 - 6 = 1.
∵点M为AC的中点,
∴MC = AM = 6,
∴AC = 12.
∵AC - BC = 4,
∴BC = 8,
∴MB = MC + BC = 6 + 8 = 14.又
∵点N为BM的中点,
∴MN = $\frac{1}{2}$BM = $\frac{1}{2}$×14 = 7,
∴CN = MN - MC = 7 - 6 = 1.
9. 【新课标 推理能力】(淄博鱼台期末)如图,∠C + ∠D = 180°,∠DAE = 3∠EBF,∠EBF = 27°,点G是AB上的一点,若∠AGF = 102°,∠BAF = 34°,下列结论错误的是( )
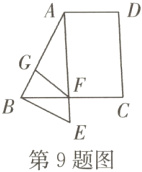
A. ∠AFB = 81°
B. ∠E = 54°
C. AD//BC
D. BE//FG

A. ∠AFB = 81°
B. ∠E = 54°
C. AD//BC
D. BE//FG
答案:
D [解析]
∵∠C + ∠D = 180°,
∴AD//BC,故选项C正确,不符合题意;
∵∠DAE = ∠CFE.
∵∠CFE = ∠EBF + ∠BEF,∠DAE = 3∠EBF,∠EBF = 27°,
∴∠CFE = 3∠EBF = 81°,∠BEF = 54°,故选项B正确,不符合题意;
∵∠AFB = ∠CFE = 81°,故选项A正确,不符合题意;
∵∠AGF = 102°,∠BAF = 34°,
∴∠AFG = 44°.
∵∠E = 54°,
∴∠AFG≠∠E,
∴BE和FG不平行,故选项D错误,符合题意.
∵∠C + ∠D = 180°,
∴AD//BC,故选项C正确,不符合题意;
∵∠DAE = ∠CFE.
∵∠CFE = ∠EBF + ∠BEF,∠DAE = 3∠EBF,∠EBF = 27°,
∴∠CFE = 3∠EBF = 81°,∠BEF = 54°,故选项B正确,不符合题意;
∵∠AFB = ∠CFE = 81°,故选项A正确,不符合题意;
∵∠AGF = 102°,∠BAF = 34°,
∴∠AFG = 44°.
∵∠E = 54°,
∴∠AFG≠∠E,
∴BE和FG不平行,故选项D错误,符合题意.
10. 【辨思维 易错题】(济宁任城期末)如图,∠COD在∠AOB的内部,且$\angle COD=\frac{1}{2}\angle AOB$,若将∠COD绕点O顺时针旋转,使∠COD在∠AOB的外部,在运动过程中,OE平分∠BOC,则∠DOE与∠AOC之间满足的数量关系是( )
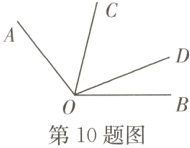
A. $2\angle DOE=\angle AOC$
B. $\angle AOC = 360° - 2\angle DOE$
C. $2\angle DOE=\angle AOC$或$\angle AOC = 360° - 2\angle DOE$
D. $2\angle DOE=\angle AOC$或$\angle AOC = 180° - 2\angle DOE$

A. $2\angle DOE=\angle AOC$
B. $\angle AOC = 360° - 2\angle DOE$
C. $2\angle DOE=\angle AOC$或$\angle AOC = 360° - 2\angle DOE$
D. $2\angle DOE=\angle AOC$或$\angle AOC = 180° - 2\angle DOE$
答案:
C [解析]设∠COD = α,∠BOE = β.如图①,当旋转角度小于180°时.因为∠COD = $\frac{1}{2}$∠AOB,所以∠AOB = 2α.因为OE平分∠BOC,所以∠BOE = ∠EOC = β,所以∠DOE = ∠EOC + ∠COD = β + α,∠AOC = ∠AOB + ∠BOC = 2α + 2β,所以2∠DOE = ∠AOC;如图②,当旋转角度大于180°时.因为∠COD = $\frac{1}{2}$∠AOB,所以∠AOB = 2α.因为OE平分∠BOC,所以∠BOE = ∠EOC = β,所以∠AOD = 360° - ∠AOB - ∠BOC - ∠COD = 360° - 3α - 2β,所以∠AOC = ∠AOD + ∠COD = 360° - 2α - 2β,∠DOE = ∠DOC + ∠COE = α + β,所以∠AOC = 360° - 2∠DOE.
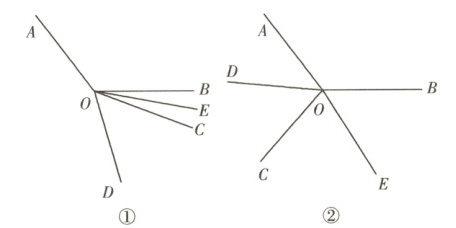
★答题策略——分类讨论
设∠COD = α,∠BOE = β,分两种情况讨论:①当旋转角度小于180°时,可求得∠DOE = ∠EOC + ∠COD = β + α,∠AOC = ∠AOB + ∠BOC = 2α + 2β;②当旋转角度大于180°时,可求得∠AOC = ∠AOD + ∠COD = 360° - 2α - 2β,∠DOE = ∠DOC + ∠COE = α + β.即可求解.
C [解析]设∠COD = α,∠BOE = β.如图①,当旋转角度小于180°时.因为∠COD = $\frac{1}{2}$∠AOB,所以∠AOB = 2α.因为OE平分∠BOC,所以∠BOE = ∠EOC = β,所以∠DOE = ∠EOC + ∠COD = β + α,∠AOC = ∠AOB + ∠BOC = 2α + 2β,所以2∠DOE = ∠AOC;如图②,当旋转角度大于180°时.因为∠COD = $\frac{1}{2}$∠AOB,所以∠AOB = 2α.因为OE平分∠BOC,所以∠BOE = ∠EOC = β,所以∠AOD = 360° - ∠AOB - ∠BOC - ∠COD = 360° - 3α - 2β,所以∠AOC = ∠AOD + ∠COD = 360° - 2α - 2β,∠DOE = ∠DOC + ∠COE = α + β,所以∠AOC = 360° - 2∠DOE.

★答题策略——分类讨论
设∠COD = α,∠BOE = β,分两种情况讨论:①当旋转角度小于180°时,可求得∠DOE = ∠EOC + ∠COD = β + α,∠AOC = ∠AOB + ∠BOC = 2α + 2β;②当旋转角度大于180°时,可求得∠AOC = ∠AOD + ∠COD = 360° - 2α - 2β,∠DOE = ∠DOC + ∠COE = α + β.即可求解.
11. (东营广饶期末)若代数式 - 2x与代数式3x - 1互为相反数,则x = _______.
答案:
1
12. 如图,把一个直径8米的圆平均分成四个扇形,再把每个扇形的弧三等分. 则点A在点O的 _______ 偏 _______ _______ °方向 _______ 米处.


答案:
北 东 30 4
查看更多完整答案,请扫码查看


