《2025年师说高中数学选择性必修第三册人教版》

1.下列两个变量中能够具有相关关系的是 （ ）
A.人的身高与受教育的程度
B.人的体重与眼睛的近视程度
C.企业员工的工号与工资
D.儿子的身高与父亲的身高

答案： 解析:对于A，人的身高与受教育的程度不具有相关关系，故A错误;对于B,人的体重与眼睛的近视程度不具有相关关系，故B错误;对于C,企业员工的工号与工资不具有相关关系，故C错误;对于D,儿子的身高与父亲的身高具有相关关系，故D正确.故选D.
答案:D

2.下图中的两个变量,具有相关关系的是 （ ）

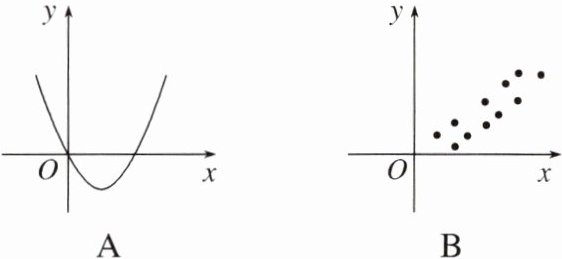
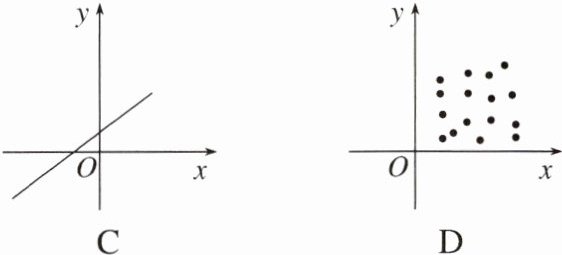
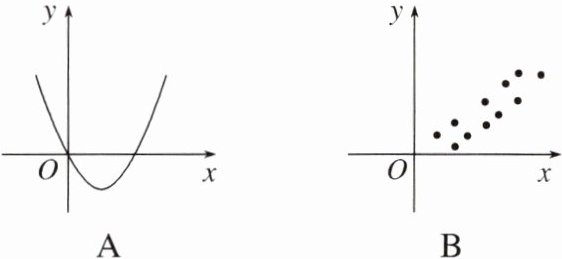
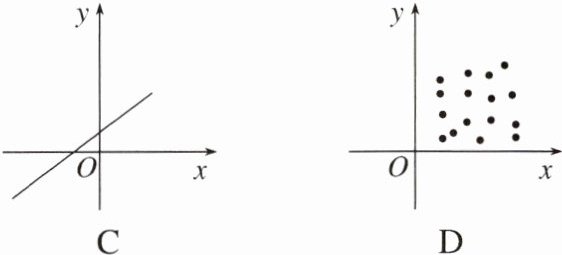
答案： 解析:相关关系是一种非确定性关系.对于A,C，两个变量具有函数关系，是一种确定性关系，故A,C错误;对于D,图中的散点分布没有什么规律，故两个变量之间不具有相关关系，故D错误;对于B,图中的散点分布在从左下角区域到右上角区域，两个变量具有相关关系，故B正确.故选B.
答案:B

3.(多选)对于任意给定的两个变量的统计数据,下列说法错误的是 （ ）

A.一定可以分析出两个变量之间的关系
B.一定可以用一条直线近似地表示两者之间的关系
C.一定可以画出散点图
D.一定可以用确定的表达式表示两者之间的关系

答案： 解析:给出两个变量的统计数据，总可以画出相应的散点图，故C中说法正确;但不一定能分析出两个变量之间的关系，更不一定符合线性相关，即不一定能用一条直线近似地表示两者之间的关系，故A，B中说法不正确;两个变量之间不一定具有函数关系，故D中说法不正确.故选ABD.
答案:ABD

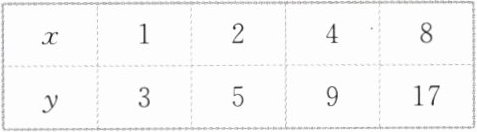
4.给出成对x,y值的数据如下：
则根据数据可以判断x和y的关系是______.(填“确定关系”“相关关系”或“没有关系”)

答案： 解析:由题表中数据可以得到$x$，$y$之间是一种函数关系，函数解析式为$y = 2x + 1$，所以$x$，$y$之间是一种确定的关系，即函数关系.
答案:确定关系

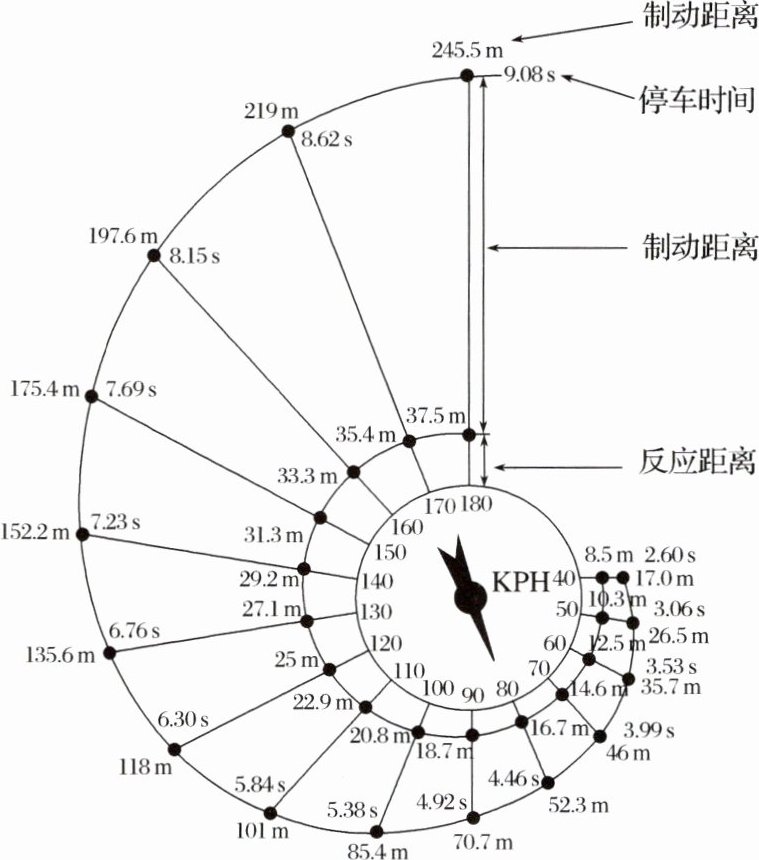
在研究急刹车的停车距离问题时,通常假定停车距离等于反应距离d1(单位:m)与制动距离d2(单位:m)之和.如图为某实验所测得的数据,其中“KPH”表示刹车时汽车的初速度v(单位:km/h).根据实验数据可以推测,下面四组函数中最适合描述d1,d2与v的函数关系的是 （ ）

A.d1 = αv,d2 = β√v
B.d1 = αv,d2 = βv²
C.d1 = α√v,d2 = βv
D.d1 = α√v,d2 = βv²

答案：
解析:设$d_1(v)=f(v)$，$d_2(v)=g(v)$.
由题图知，$d_1(v)=f(v)$过点$(40,8.5)$，$(50,10.3)$，$(60,12.5)$，$(70,14.6)$，$(80,16.7)$，$(90,18.7)$，$(100,20.8)$，$(110,22.9)$，$(120,25)$，$(130,27.1)$，$(140,29.2)$，$(150,31.3)$，$(160,33.3)$，$(170,35.4)$，$(180,37.5)$.
作出散点图，如图①.

由图①可得，$d_1$与$v$呈现线性关系，可选择用$d_1=\alpha v$.
$d_2(v)=g(v)$过点$(40,8.5)$，$(50,16.2)$，$(60,23.2)$，$(70,31.4)$，$(80,35.6)$，$(90,52)$，$(100,64.6)$，$(110,78.1)$，$(120,93)$，$(130,108.5)$，$(140,123)$，$(150,144.1)$，$(160,164.3)$，$(170,183.6)$，$(180,208)$.
作出散点图，如图②.

由图②可得，$d_2$与$v$呈现非线性关系，比较之下，可选择用$d_2=\beta v^2$.故选B.
答案:B