《2025年师说高中数学选择性必修第三册人教版》

例 3 （1）如图，一环形花坛分成 A，B，C，D 四块，现有四种不同的花供选种，要求在每块花坛里种一种花，且相邻的两块花坛种不同的花，则不同的种法数为 （ ）

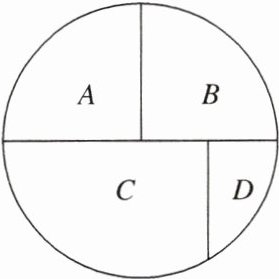
A.108 B.96 C.72 D.48
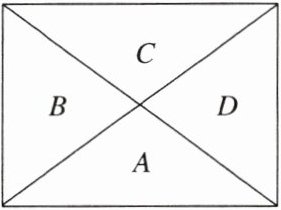
（2）用红、黄、蓝三种不同颜色给如图所示的 4 块区域 A、B、C、D 涂色，要求同一区域用同一种颜色，有公共边的区域使用不同颜色，则共有涂色方法 （ ）
A.14 种 B.16 种 C.20 种 D.18 种

答案： 解析:
(1)完成这件事情需要四步，第一步，A地块有4种选择;第二步，B地块有3种选择;第三步，C地块有2种选择;第四步,D地块有2种选择，共有4×3×2×2=48(种).故选D.
(2)先涂A,有3种涂法，再涂B有2种涂法，涂C时，与A 同色，有1种涂法，此时D有2种涂法，当C与A异色时有1种涂法，这时D有1种涂法，所以共有3×2×(1×2+1×1)=18(种).故选D.
答案:
(1)D　
(2)D

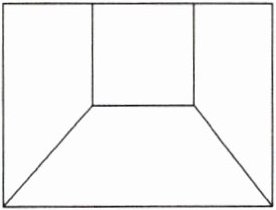
跟踪训练 3 某学校有一块绿化用地，其形状如图所示.为了让效果更美观，要求在四个区域内种植花卉，且相邻区域颜色不同.现有五种不同颜色的花卉可供选择，则不同的种植方案共有________种.（用数字作答）

答案：
解析:先在1中种植，有5种不同的种植方法，再在2中种植，有4种不同的种植方法，

再在3中种植，有3种不同的种植方法，最后在4中种植，有3种不同的种植方法，
所以不同的种植方法共有5×4×3×3=180(种).
答案:180

1.由数字 1，2，3，4 构成的三位数有 （ ）
A.4³ 个
B.3⁴ 个
C.4×3×2 个
D.1×2×3 个

答案： 解析:百位有4种选择，十位有4种选择，个位有4种选择，故构成的三位数共有4³个.故选A.
答案:A

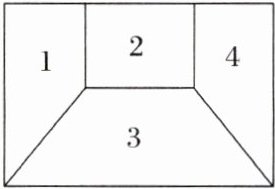
2.如图所示，用 6 种不同的颜色给图中的 4 个格子涂色，每个格子涂一种颜色，要求相邻的两个格子颜色不同，则不同的涂色方法共有( )种.

A.480
B.600
C.360
D.750

答案： 解析:首先给最左边的一个格子涂色，有6种选择，左边第二个格子有5种选择，第三个格子有5种选择，第四个格子也有5种选择，根据分步乘法计数原理，共有6×5×5×5=750(种)涂色方法.故选D.
答案:D

3.5 人排一个 5 天的值日表，每天排一人值日，每人可以排多天或不排，但相邻两天不能排同一人，值日表排法的总数为 （ ）
A.120
B.324
C.720
D.1 280

答案： 解析:第一天可以排5个人中的任意一个，有5种排法;第二天可以排另外4个人中任意一个，有4种排法;第三天同上，有4种排法;第四天同上，有4种排法;第五天同上，有4种排法.根据分步乘法计数原理，所有的排法总数为5×4×4×4×4=1280.故选D.
答案:D

4.从 4 种蔬菜品种中选出 3 种，分别种植在 3 块不同土质的土地上，则不同的种植方法有________种.

答案： 解析:按3块土地依次种植分三步，第一块土地上有4种种植方法，第二块土地上有3种种植方法，第三块土地上有2 种种植方法，所以不同的种植方法共有4×3×2=24(种).答案:24

如果一个三位正整数如“a₁a₂a₃”满足 a₁＞a₂，且 a₂＜a₃，则称这样的三位数为“好数”（如 201，325 等），那么由数字 1，2，3，4，5 能组成____________个无重复数字的“好数”.
指津：讨论首位分别为 1、2、3、4、5，再依次安排中间位置上的数字，并求出对应好数的个数，最后加总即可.

答案： 解析:当首位为2，中间位置为1有3个好数;
当首位为3，中间位置为1有3个好数，中间位置为2有2个好数;
当首位为4，中间位置为1有3个好数，中间位置为2有2个好数，中间位置为3有1个好数;
当首位为5，中间位置为1有3个好数，中间位置为2有2个好数，中间位置为3有1个好数.
综上，共有20个无重复数字的好数.
答案:20