2025年师说高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年师说高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
跟踪训练2 某公司的一次招聘中,应聘者都要经过
A、B、C三个独立项目的测试,如果通过其中的两个或三个项目的测试即可被录用.若甲、乙、丙三人通过每个项目测试的概率都是$\frac{1}{2}$.
(1)求甲被录用的概率;
(2)设甲、乙、丙三人中被录用的人数为X,求X的分布列.
A、B、C三个独立项目的测试,如果通过其中的两个或三个项目的测试即可被录用.若甲、乙、丙三人通过每个项目测试的概率都是$\frac{1}{2}$.
(1)求甲被录用的概率;
(2)设甲、乙、丙三人中被录用的人数为X,求X的分布列.
答案:
解析:
(1)通过两个项目测试的概率为$C_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{3}{8}$,
通过三个项目测试的概率为$C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$,
则甲被录用的概率为$\frac{3}{8}+\frac{1}{8}=\frac{1}{2}$.
(2)由于甲、乙、丙三人通过每个项目测试的概率都是$\frac{1}{2}$,由此知甲、乙、丙被录用的概率都是$\frac{1}{2}$,所以$X\sim B(3,\frac{1}{2})$,
所以$P(X = 0) = C_{3}^{0}(\frac{1}{2})^{3}=\frac{1}{8}$,
$P(X = 1) = C_{3}^{1}\frac{1}{2}×(\frac{1}{2})^{2}=\frac{3}{8}$,
$P(X = 2) = C_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{3}{8}$,
$P(X = 3) = C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$.
所以X的分布列为
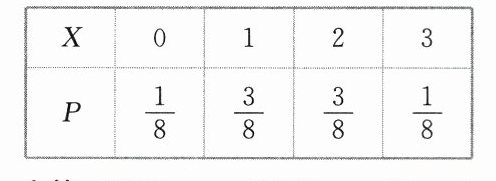
解析:
(1)通过两个项目测试的概率为$C_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{3}{8}$,
通过三个项目测试的概率为$C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$,
则甲被录用的概率为$\frac{3}{8}+\frac{1}{8}=\frac{1}{2}$.
(2)由于甲、乙、丙三人通过每个项目测试的概率都是$\frac{1}{2}$,由此知甲、乙、丙被录用的概率都是$\frac{1}{2}$,所以$X\sim B(3,\frac{1}{2})$,
所以$P(X = 0) = C_{3}^{0}(\frac{1}{2})^{3}=\frac{1}{8}$,
$P(X = 1) = C_{3}^{1}\frac{1}{2}×(\frac{1}{2})^{2}=\frac{3}{8}$,
$P(X = 2) = C_{3}^{2}(\frac{1}{2})^{2}×\frac{1}{2}=\frac{3}{8}$,
$P(X = 3) = C_{3}^{3}(\frac{1}{2})^{3}=\frac{1}{8}$.
所以X的分布列为

师问:若随机变量X服从二项分布B(n,p),那么X的均值和方差是什么?
生答:
生答:
答案:
$E(X)=np;D(X)=np(1 - p)$.
例3 一出租车司机从某饭店到火车站途中有5个交通岗,假设他在各交通岗遇到红灯这一事件是相互独立的,并且概率是$\frac{1}{3}$.
(1)求这位司机遇到红灯数X的均值与方差.
(2)若遇上红灯,则需等待30秒,求司机总共等待时间Y的均值与方差.
(1)求这位司机遇到红灯数X的均值与方差.
(2)若遇上红灯,则需等待30秒,求司机总共等待时间Y的均值与方差.
答案:
解析:
(1)由题意得这位司机遇到红灯数X服从二项分布$X\sim B(5,\frac{1}{3})$,
所以$E(X)=5×\frac{1}{3}=\frac{5}{3}$,$D(X)=5×\frac{1}{3}×(1 - \frac{1}{3})=\frac{10}{9}$.
(2)由题意得Y = 30X,由
(1)得$E(X)=\frac{5}{3}$,$D(X)=\frac{10}{9}$,
所以$E(Y)=30E(X)=30×\frac{5}{3}=50$,$D(Y)=30^{2}·D(X)=900×\frac{10}{9}=1000$.
(1)由题意得这位司机遇到红灯数X服从二项分布$X\sim B(5,\frac{1}{3})$,
所以$E(X)=5×\frac{1}{3}=\frac{5}{3}$,$D(X)=5×\frac{1}{3}×(1 - \frac{1}{3})=\frac{10}{9}$.
(2)由题意得Y = 30X,由
(1)得$E(X)=\frac{5}{3}$,$D(X)=\frac{10}{9}$,
所以$E(Y)=30E(X)=30×\frac{5}{3}=50$,$D(Y)=30^{2}·D(X)=900×\frac{10}{9}=1000$.
跟踪训练3 某一中学生心理咨询中心服务电话的接通率为$\frac{3}{4}$,某班3名同学商定明天分别就同一问题询问该服务中心,且每人只拨打一次.
(1)求他们中成功咨询的人数X的分布列;
(2)求E(X)与D(X)的值.
(1)求他们中成功咨询的人数X的分布列;
(2)求E(X)与D(X)的值.
答案:
解析:
(1)依题意知$X\sim B(3,\frac{3}{4})$,
且$P(X = k) = C_{3}^{k}×(\frac{3}{4})^{k}×(\frac{1}{4})^{3 - k},k = 0,1,2,3$,
$P(X = 0) = C_{3}^{0}×(\frac{3}{4})^{0}×(\frac{1}{4})^{3}=\frac{1}{64}$,
$P(X = 1) = C_{3}^{1}×\frac{3}{4}×(\frac{1}{4})^{2}=\frac{9}{64}$,
$P(X = 2) = C_{3}^{2}×(\frac{3}{4})^{2}×\frac{1}{4}=\frac{27}{64}$,
$P(X = 3) = C_{3}^{3}×(\frac{3}{4})^{3}=\frac{27}{64}$.
∴X的分布列为
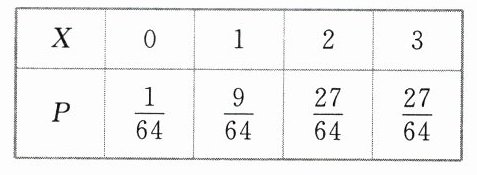
(2)由$X\sim B(3,\frac{3}{4})$及二项分布的性质得,
$E(X)=np=3×\frac{3}{4}=\frac{9}{4}$,
$D(X)=np(1 - p)=3×\frac{3}{4}×(1 - \frac{3}{4})=\frac{9}{16}$.
解析:
(1)依题意知$X\sim B(3,\frac{3}{4})$,
且$P(X = k) = C_{3}^{k}×(\frac{3}{4})^{k}×(\frac{1}{4})^{3 - k},k = 0,1,2,3$,
$P(X = 0) = C_{3}^{0}×(\frac{3}{4})^{0}×(\frac{1}{4})^{3}=\frac{1}{64}$,
$P(X = 1) = C_{3}^{1}×\frac{3}{4}×(\frac{1}{4})^{2}=\frac{9}{64}$,
$P(X = 2) = C_{3}^{2}×(\frac{3}{4})^{2}×\frac{1}{4}=\frac{27}{64}$,
$P(X = 3) = C_{3}^{3}×(\frac{3}{4})^{3}=\frac{27}{64}$.
∴X的分布列为

(2)由$X\sim B(3,\frac{3}{4})$及二项分布的性质得,
$E(X)=np=3×\frac{3}{4}=\frac{9}{4}$,
$D(X)=np(1 - p)=3×\frac{3}{4}×(1 - \frac{3}{4})=\frac{9}{16}$.
1.在100件产品中有5件次品,采用放回的方式从中任意抽取10件,设X表示这10件产品中的次品数,则 ( )
A.X~B(100,0.05) B.X~B(10,0.05)
C.X~B(1000,95) D.X~B(10,0.95)
A.X~B(100,0.05) B.X~B(10,0.05)
C.X~B(1000,95) D.X~B(10,0.95)
答案:
解析:有放回抽取,每次取到次品的概率都是$\frac{5}{100}=0.05$,相当于10次独立重复的伯努利实验,所以服从二项分布$X\sim B(10,0.05)$.故选B.
答案:B
答案:B
2.某一批种子的发芽率为$\frac{2}{3}$.从中随机选择3颗种子进行播种,那么恰有2颗种子发芽的概率为 ( )
A.$\frac{2}{9}$
B.$\frac{8}{27}$
C.$\frac{4}{9}$
D.$\frac{2}{3}$
A.$\frac{2}{9}$
B.$\frac{8}{27}$
C.$\frac{4}{9}$
D.$\frac{2}{3}$
答案:
解析:由题意可知种子发芽的颗数X服从二项分布$X\sim B(3,\frac{2}{3})$,所以恰好有2颗种子发芽的概率为$C_{3}^{2}(\frac{2}{3})^{2}×\frac{1}{3}=\frac{4}{9}$.故选C.
答案:C
答案:C
3.已知随机变量S服从二项分布S~B(6,$\frac{1}{3}$),即P(S=2)等于 ( )
A.$\frac{3}{16}$
B.$\frac{1}{243}$
C.$\frac{13}{243}$
D.$\frac{80}{243}$
A.$\frac{3}{16}$
B.$\frac{1}{243}$
C.$\frac{13}{243}$
D.$\frac{80}{243}$
答案:
解析:因为随机变量$\xi$服从二项分布$\xi\sim B(6,\frac{1}{3})$,
所以$P(\xi = 2) = C_{6}^{2}(\frac{1}{3})^{2}(\frac{2}{3})^{4}=\frac{80}{243}$.故选D.
答案:D
所以$P(\xi = 2) = C_{6}^{2}(\frac{1}{3})^{2}(\frac{2}{3})^{4}=\frac{80}{243}$.故选D.
答案:D
4.已知随机变量X服从二项分布B(n,p),且X的期望E(X)=4,方差D(X)=2,则n=________.
答案:
解析:依题意$X\sim B(n,p)$,所以$E(X)=np = 4$,$D(X)=np(1 - p)=2$,解得$p=\frac{1}{2}$,$n = 8$.
答案:8
答案:8
在荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是 ( )
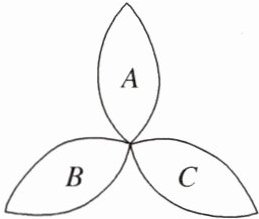
A.$\frac{4}{81}$ B.$\frac{8}{81}$ C.$\frac{16}{81}$ D.$\frac{8}{27}$

A.$\frac{4}{81}$ B.$\frac{8}{81}$ C.$\frac{16}{81}$ D.$\frac{8}{27}$
答案:
解析:因为逆时针方向跳的概率是顺时针方向跳的概率的两倍,所以逆时针方向跳的概率是$\frac{2}{3}$,顺时针方向跳的概率是$\frac{1}{3}$,若青蛙在A叶上,则跳四次之后停在A叶上,则满足四次跳跃中有2次是顺时针方向跳,有2次是逆时针跳.若先按逆时针开始从A→B,则剩余3次中有1次是按逆时针,其余2次按顺时针跳,则对应的概率为$\frac{2}{3}×C_{3}^{1}×\frac{2}{3}×(\frac{1}{3})^{2}=\frac{4}{27}$;若先按顺时针开始从A→C,则剩余3次中有1次是按顺时针,其余2次按逆时针跳,则对应的概率为$\frac{1}{3}×C_{3}^{1}×\frac{1}{3}×(\frac{2}{3})^{2}=\frac{4}{27}$.故跳四次之后停在A叶上的概率为$\frac{4}{27}+\frac{4}{27}=\frac{8}{27}$.故选D.
答案:D
答案:D
温馨提示:请完成课时作业18
答案:
查看更多完整答案,请扫码查看


