2025年师说高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年师说高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
师问:如果X是一个离散型随机变量,X加一个常数或乘一个常数后,其均值会怎样变化?
即E(X + b)和E(aX)(其中a,b为常数)分别与E(X)有怎样的关系?
即E(X + b)和E(aX)(其中a,b为常数)分别与E(X)有怎样的关系?
答案:
设离散型随机变量$X$的分布列为
$X$ $x_1$ $x_2$ $\cdots$ $x_i$ $\cdots$ $x_n$
$P$ $p_1$ $p_2$ $\cdots$ $p_i$ $\cdots$ $p_n$
则$E(X + b)=(x_1 + b)p_1+(x_2 + b)p_2+\cdots+(x_n + b)p_n$
$=(x_1p_1 + x_2p_2+\cdots+x_np_n)+b(p_1 + p_2+\cdots+p_n)$
$=E(X)+b$.
类似地,可得$E(aX)=aE(X)$.
$X$ $x_1$ $x_2$ $\cdots$ $x_i$ $\cdots$ $x_n$
$P$ $p_1$ $p_2$ $\cdots$ $p_i$ $\cdots$ $p_n$
则$E(X + b)=(x_1 + b)p_1+(x_2 + b)p_2+\cdots+(x_n + b)p_n$
$=(x_1p_1 + x_2p_2+\cdots+x_np_n)+b(p_1 + p_2+\cdots+p_n)$
$=E(X)+b$.
类似地,可得$E(aX)=aE(X)$.
例2 已知随机变量X的分布列为

(1)求m的值;
(2)求E(X);
(3)若Y = 2X-3,求E(Y).

(1)求m的值;
(2)求E(X);
(3)若Y = 2X-3,求E(Y).
答案:
解析:
(1)依题意,由分布列得$\frac{1}{4}+\frac{1}{3}+\frac{1}{5}+m+\frac{1}{20}=1$,解得$m=\frac{1}{6}$,
所以$m$的值为$\frac{1}{6}$.
(2)由
(1)得$E(X)=-2\times\frac{1}{4}+(-1)\times\frac{1}{3}+0\times\frac{1}{5}+1\times\frac{1}{6}+2\times\frac{1}{20}=-\frac{17}{30}$.
(3)方法一 因为$Y = 2X - 3$,
所以$E(Y)=2E(X)-3=2\times(-\frac{17}{30})-3=-\frac{62}{15}$.
方法二 因为$Y = 2X - 3$,所以$Y$的分布列为
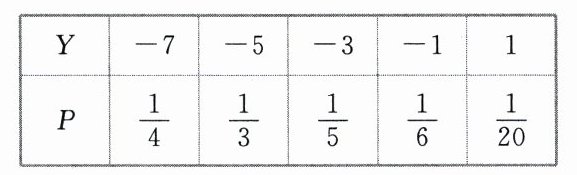
所以$E(Y)=-7\times\frac{1}{4}+(-5)\times\frac{1}{3}+(-3)\times\frac{1}{5}+(-1)\times\frac{1}{6}+1\times\frac{1}{20}=-\frac{62}{15}$.
解析:
(1)依题意,由分布列得$\frac{1}{4}+\frac{1}{3}+\frac{1}{5}+m+\frac{1}{20}=1$,解得$m=\frac{1}{6}$,
所以$m$的值为$\frac{1}{6}$.
(2)由
(1)得$E(X)=-2\times\frac{1}{4}+(-1)\times\frac{1}{3}+0\times\frac{1}{5}+1\times\frac{1}{6}+2\times\frac{1}{20}=-\frac{17}{30}$.
(3)方法一 因为$Y = 2X - 3$,
所以$E(Y)=2E(X)-3=2\times(-\frac{17}{30})-3=-\frac{62}{15}$.
方法二 因为$Y = 2X - 3$,所以$Y$的分布列为

所以$E(Y)=-7\times\frac{1}{4}+(-5)\times\frac{1}{3}+(-3)\times\frac{1}{5}+(-1)\times\frac{1}{6}+1\times\frac{1}{20}=-\frac{62}{15}$.
跟踪训练2 (1)已知随机变量X的概率分布列为
P(X = n)=a$\sin\frac{\pi}{4n - 2}$(n = 1,2),其中a是常数,
则E($\frac{1}{a}X$) = ( )
A.$\frac{2}{3}$ B.$\frac{4}{3}$ C.2 D.$\frac{8}{9}$
(2)已知随机变量X的分布列为

且Y = aX + 3,若E(Y)=-2,则a等于 ( )
A.-3 B.-2 C.$\frac{5}{3}$ D.3
P(X = n)=a$\sin\frac{\pi}{4n - 2}$(n = 1,2),其中a是常数,
则E($\frac{1}{a}X$) = ( )
A.$\frac{2}{3}$ B.$\frac{4}{3}$ C.2 D.$\frac{8}{9}$
(2)已知随机变量X的分布列为

且Y = aX + 3,若E(Y)=-2,则a等于 ( )
A.-3 B.-2 C.$\frac{5}{3}$ D.3
答案:
解析:
(1)由$P(X = n)=a\sin\frac{\pi}{4n - 2}(n = 1,2)$,得$P(X = 1)=a$,$P(X = 2)=\frac{1}{2}a$,
由$P(X = 1)+P(X = 2)=1$,得$a=\frac{2}{3}$,
于是$E(X)=1\times P(X = 1)+2\times P(X = 2)=2a=\frac{4}{3}$,
所以$E(\frac{1}{a}X)=\frac{3}{2}E(X)=2$. 故选C.
(2)结合题意,$E(X)=1\times\frac{1}{2}+2\times\frac{1}{3}+3\times\frac{1}{6}=\frac{5}{3}$,因为$Y = aX + 3$,所以$E(Y)=aE(X)+3=\frac{5}{3}a+3=-2$,解得$a=-3$. 故选A.
答案:
(1)C
(2)A
(1)由$P(X = n)=a\sin\frac{\pi}{4n - 2}(n = 1,2)$,得$P(X = 1)=a$,$P(X = 2)=\frac{1}{2}a$,
由$P(X = 1)+P(X = 2)=1$,得$a=\frac{2}{3}$,
于是$E(X)=1\times P(X = 1)+2\times P(X = 2)=2a=\frac{4}{3}$,
所以$E(\frac{1}{a}X)=\frac{3}{2}E(X)=2$. 故选C.
(2)结合题意,$E(X)=1\times\frac{1}{2}+2\times\frac{1}{3}+3\times\frac{1}{6}=\frac{5}{3}$,因为$Y = aX + 3$,所以$E(Y)=aE(X)+3=\frac{5}{3}a+3=-2$,解得$a=-3$. 故选A.
答案:
(1)C
(2)A
例3 某环保机器制造商为响应号召,对一次购买2台机器的客户推出了两种超过机器保修期后5年内的延保维修方案:
方案一:交纳延保金5 000元,在延保的5年内可免费维修2次,超过2次每次收取维修费1 000元;
方案二:交纳延保金6 230元,在延保的5和内可免费维修4次,超过4次每次收取维修费t元;
制造商为制定的收取标准,为此搜集并整理了200台这种机器超过保修期后5年内维修的次数,统计得到下表
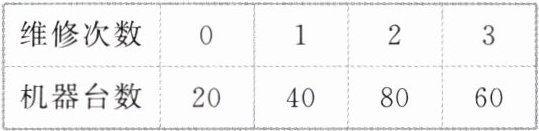
以这200台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示2台机器超过保修期后5年内共需维修的次数.
(1)求X的分布列;
(2)以所需延保金与维修费用之和的均值为决策依据,为使选择方案二对客户更合算,应把t定在什么范围?
方案一:交纳延保金5 000元,在延保的5年内可免费维修2次,超过2次每次收取维修费1 000元;
方案二:交纳延保金6 230元,在延保的5和内可免费维修4次,超过4次每次收取维修费t元;
制造商为制定的收取标准,为此搜集并整理了200台这种机器超过保修期后5年内维修的次数,统计得到下表

以这200台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示2台机器超过保修期后5年内共需维修的次数.
(1)求X的分布列;
(2)以所需延保金与维修费用之和的均值为决策依据,为使选择方案二对客户更合算,应把t定在什么范围?
答案:
解析:
(1)由题意得,$X = 0,1,2,3,4,5,6$,
$P(X = 0)=\frac{1}{10}\times\frac{1}{10}=\frac{1}{100}$,
$P(X = 1)=\frac{1}{10}\times\frac{1}{5}\times2=\frac{1}{25}$,
$P(X = 2)=\frac{1}{10}\times\frac{2}{5}\times2+\frac{1}{5}\times\frac{1}{5}=\frac{3}{25}$,
$P(X = 3)=\frac{1}{10}\times\frac{3}{10}\times2+\frac{1}{5}\times\frac{2}{5}\times2=\frac{11}{50}$,
$P(X = 4)=\frac{3}{10}\times\frac{1}{5}\times2+\frac{2}{5}\times\frac{2}{5}=\frac{7}{25}$,
$P(X = 5)=\frac{3}{10}\times\frac{2}{5}\times2=\frac{6}{25}$,
$P(X = 6)=\frac{3}{10}\times\frac{3}{10}=\frac{9}{100}$,
$\therefore X$的分布列为

(2)选择方案一,所需费用为$Y_1$元,则$X\leq2$时,$Y_1 = 5000$;$X = 3$时,$Y_1 = 6000$;$X = 4$时,$Y_1 = 7000$;$X = 5$时,$Y_5 = 8000$;$X = 6$时,$Y_1 = 9000$.
$\therefore Y_1$的分布列为

$E(Y_1)=5000\times\frac{17}{100}+6000\times\frac{11}{50}+7000\times\frac{7}{25}+8000\times\frac{6}{25}+9000\times\frac{9}{100}=6860$.
选择方案二,所需费用为$Y_2$元,则$X\leq4$时,$Y_2 = 6230$;$X = 5$时,$Y_2 = 6230 + t$;$X = 6$时,$Y_2 = 6230 + 2t$,则$Y_2$的分布列为
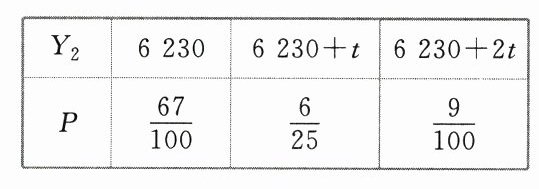
$E(Y_2)=6230\times\frac{67}{100}+(6230 + t)\times\frac{6}{25}+(6230 + 2t)\times\frac{9}{100}=6230+\frac{21t}{50}$.
要使选择方案二对客户更合算,则$E(Y_2)\lt E(Y_1)$,
$\therefore 6230+\frac{21t}{50}\lt6860$,解得$t\lt1500$,即$t$的取值范围为$[0,1500)$.
解析:
(1)由题意得,$X = 0,1,2,3,4,5,6$,
$P(X = 0)=\frac{1}{10}\times\frac{1}{10}=\frac{1}{100}$,
$P(X = 1)=\frac{1}{10}\times\frac{1}{5}\times2=\frac{1}{25}$,
$P(X = 2)=\frac{1}{10}\times\frac{2}{5}\times2+\frac{1}{5}\times\frac{1}{5}=\frac{3}{25}$,
$P(X = 3)=\frac{1}{10}\times\frac{3}{10}\times2+\frac{1}{5}\times\frac{2}{5}\times2=\frac{11}{50}$,
$P(X = 4)=\frac{3}{10}\times\frac{1}{5}\times2+\frac{2}{5}\times\frac{2}{5}=\frac{7}{25}$,
$P(X = 5)=\frac{3}{10}\times\frac{2}{5}\times2=\frac{6}{25}$,
$P(X = 6)=\frac{3}{10}\times\frac{3}{10}=\frac{9}{100}$,
$\therefore X$的分布列为

(2)选择方案一,所需费用为$Y_1$元,则$X\leq2$时,$Y_1 = 5000$;$X = 3$时,$Y_1 = 6000$;$X = 4$时,$Y_1 = 7000$;$X = 5$时,$Y_5 = 8000$;$X = 6$时,$Y_1 = 9000$.
$\therefore Y_1$的分布列为

$E(Y_1)=5000\times\frac{17}{100}+6000\times\frac{11}{50}+7000\times\frac{7}{25}+8000\times\frac{6}{25}+9000\times\frac{9}{100}=6860$.
选择方案二,所需费用为$Y_2$元,则$X\leq4$时,$Y_2 = 6230$;$X = 5$时,$Y_2 = 6230 + t$;$X = 6$时,$Y_2 = 6230 + 2t$,则$Y_2$的分布列为

$E(Y_2)=6230\times\frac{67}{100}+(6230 + t)\times\frac{6}{25}+(6230 + 2t)\times\frac{9}{100}=6230+\frac{21t}{50}$.
要使选择方案二对客户更合算,则$E(Y_2)\lt E(Y_1)$,
$\therefore 6230+\frac{21t}{50}\lt6860$,解得$t\lt1500$,即$t$的取值范围为$[0,1500)$.
查看更多完整答案,请扫码查看


