2025年师说高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年师说高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第37页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
师问:某商场要将单价分别为18元/千克、24元/千克、36元/千克的3种糖果按3∶2∶1的比例混合销售,如何对混合糖果定价才合理?
生答:
生答:
答案:
由于平均在每1千克的混合糖果中,3种糖果的质量分别是$\frac{1}{2}$千克、$\frac{1}{3}$千克和$\frac{1}{6}$千克,所以混合糖果的合理价格应该是$18\times\frac{1}{2}+24\times\frac{1}{3}+36\times\frac{1}{6}=23$(元/千克).
这里的23元/千克就是混合糖果价格的均值.
这里的23元/千克就是混合糖果价格的均值.
例1 某学校食堂提供甲、乙、丙三种套餐,每日随机供应一种,且相邻两天不重复.已知食堂今天供应套餐甲,用随机变量X表示接下来的三天中食堂供应套餐乙的天数,求X的分布列与期望.
答案:
解析:$X$的所有可能取值分别为0,1,2,
则$P(X = 0)=\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}$,
$P(X = 2)=\frac{1}{2}\times1\times\frac{1}{2}=\frac{1}{4}$,
$P(X = 1)=1-\frac{1}{4}-\frac{1}{8}=\frac{5}{8}$,
$X$的分布列为
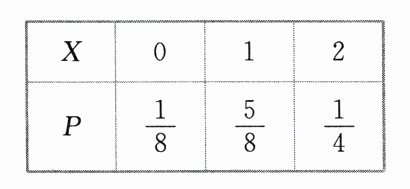
所以$X$的期望为$E(X)=0\times\frac{1}{8}+1\times\frac{5}{8}+2\times\frac{1}{4}=\frac{9}{8}$.
解析:$X$的所有可能取值分别为0,1,2,
则$P(X = 0)=\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}$,
$P(X = 2)=\frac{1}{2}\times1\times\frac{1}{2}=\frac{1}{4}$,
$P(X = 1)=1-\frac{1}{4}-\frac{1}{8}=\frac{5}{8}$,
$X$的分布列为

所以$X$的期望为$E(X)=0\times\frac{1}{8}+1\times\frac{5}{8}+2\times\frac{1}{4}=\frac{9}{8}$.
跟踪训练1 已知盒中有2个黑球和2个白球,每次从盒中不放回地随机摸取1个球,只要摸到白球就停止摸球.记摸球的次数为随机变量X,求X的分布列和期望.
答案:
解析:$X$的所有可能取值分别为1,2,3,
$P(X = 1)=\frac{2}{4}=\frac{1}{2}$,$P(X = 2)=\frac{2}{4}\times\frac{2}{3}=\frac{1}{3}$,
$P(X = 3)=\frac{1}{6}$,
所以$X$的分布列为

$E(X)=\frac{1}{2}+\frac{2}{3}+\frac{3}{6}=\frac{5}{3}$.
解析:$X$的所有可能取值分别为1,2,3,
$P(X = 1)=\frac{2}{4}=\frac{1}{2}$,$P(X = 2)=\frac{2}{4}\times\frac{2}{3}=\frac{1}{3}$,
$P(X = 3)=\frac{1}{6}$,
所以$X$的分布列为

$E(X)=\frac{1}{2}+\frac{2}{3}+\frac{3}{6}=\frac{5}{3}$.
查看更多完整答案,请扫码查看


