2025年师说高中数学选择性必修第三册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年师说高中数学选择性必修第三册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
例3 某学校参加某项竞赛仅有一个名额,结合平时训练成绩,甲、乙两名学生进入最后选拔,学校为此设计了如下选拔方案:设计6道题进行测试,若这6道题中,甲能正确解答其中的4道,乙能正确解答每个题目的概率均为$\frac{2}{3}$,假设甲、乙两名学生解答每道测试题都相互独立、互不影响,现甲、乙从这6道测试题中分别随机抽取3题进行解答.
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量$X$,求$X$的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
(1)求甲、乙共答对2道题目的概率;
(2)设甲答对题数为随机变量$X$,求$X$的分布列、数学期望和方差;
(3)从数学期望和方差的角度分析,应选拔哪个学生代表学校参加竞赛?
答案:
解析:
(1)由题意得甲、乙两名学生共答对2个问题的概率:
$P=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}\times C_{3}^{0}\times(\frac{2}{3})^{0}\times(\frac{1}{3})^{3}+\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}\times C_{3}^{1}\times\frac{2}{3}\times(\frac{1}{3})^{2}=\frac{1}{15}$。
(2)设学生甲答对的题数为$X$,则$X$的所有可能取值为$1,2,3$。
$P(X = 1)=\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}=\frac{1}{5}$,$P(X = 2)=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}=\frac{3}{5}$,$P(X = 3)=\frac{C_{4}^{3}}{C_{6}^{3}}=\frac{1}{5}$。
$X$的分布列为
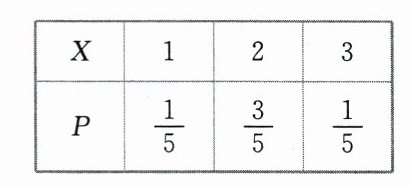
所以$E(X)=1\times\frac{1}{5}+2\times\frac{3}{5}+3\times\frac{1}{5}=2$。
$D(X)=\frac{1}{5}(1 - 2)^{2}+\frac{3}{5}(2 - 2)^{2}+\frac{1}{5}(3 - 2)^{2}=\frac{2}{5}$。
(3)设学生乙答对的题数为$Y$,则$Y$的所有可能取值为$0,1,2,3$,则$Y\sim B(3,\frac{2}{3})$。
所以$E(Y)=3\times\frac{2}{3}=2$,$D(Y)=3\times\frac{2}{3}\times(1 - \frac{2}{3})=\frac{2}{3}$。
因为$E(X)=E(Y)$,$D(X)<D(Y)$,即甲、乙答对的题目数一样,但甲较稳定,
所以应选拔甲学生代表学校参加竞赛。
解析:
(1)由题意得甲、乙两名学生共答对2个问题的概率:
$P=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}\times C_{3}^{0}\times(\frac{2}{3})^{0}\times(\frac{1}{3})^{3}+\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}\times C_{3}^{1}\times\frac{2}{3}\times(\frac{1}{3})^{2}=\frac{1}{15}$。
(2)设学生甲答对的题数为$X$,则$X$的所有可能取值为$1,2,3$。
$P(X = 1)=\frac{C_{4}^{1}C_{2}^{2}}{C_{6}^{3}}=\frac{1}{5}$,$P(X = 2)=\frac{C_{4}^{2}C_{2}^{1}}{C_{6}^{3}}=\frac{3}{5}$,$P(X = 3)=\frac{C_{4}^{3}}{C_{6}^{3}}=\frac{1}{5}$。
$X$的分布列为

所以$E(X)=1\times\frac{1}{5}+2\times\frac{3}{5}+3\times\frac{1}{5}=2$。
$D(X)=\frac{1}{5}(1 - 2)^{2}+\frac{3}{5}(2 - 2)^{2}+\frac{1}{5}(3 - 2)^{2}=\frac{2}{5}$。
(3)设学生乙答对的题数为$Y$,则$Y$的所有可能取值为$0,1,2,3$,则$Y\sim B(3,\frac{2}{3})$。
所以$E(Y)=3\times\frac{2}{3}=2$,$D(Y)=3\times\frac{2}{3}\times(1 - \frac{2}{3})=\frac{2}{3}$。
因为$E(X)=E(Y)$,$D(X)<D(Y)$,即甲、乙答对的题目数一样,但甲较稳定,
所以应选拔甲学生代表学校参加竞赛。
跟踪训练3 某商场举行有奖促销活动,凡7月7日当天消费每超过400元(含400元),均可抽奖一次,抽奖箱里有6个形状、大小、质地完全相同的小球,其中红球有3个,白球有3个,抽奖方案设置两种,顾客自行选择其中的一种方案.
方案一:从抽奖箱中,一次性摸出2个球,若摸出2个红球,则打6折;若摸出1个红球,则打8折;若没摸出红球,则不打折
方案二:从抽奖箱中,有放回地每次摸取1个球,连摸2次,每摸到1次红球,立减80元.
(1)若小方、小红均分别消费了400元,且均选择抽奖方案一,试求他们其中恰有一人享受6折优惠的概率;
(2)若小勇消费恰好满500元,试比较说明小勇选择哪种方案更划算.
方案一:从抽奖箱中,一次性摸出2个球,若摸出2个红球,则打6折;若摸出1个红球,则打8折;若没摸出红球,则不打折
方案二:从抽奖箱中,有放回地每次摸取1个球,连摸2次,每摸到1次红球,立减80元.
(1)若小方、小红均分别消费了400元,且均选择抽奖方案一,试求他们其中恰有一人享受6折优惠的概率;
(2)若小勇消费恰好满500元,试比较说明小勇选择哪种方案更划算.
答案:
解析:
(1)由题意,设顾客享受到6折优惠为事件$A$,则$P(A)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$。
$\therefore$小方、小红两人其中有一人享受6折优惠的概率为
$P = C_{2}^{1}\cdot P(A)\cdot[1 - P(A)]=2\times\frac{1}{5}\times(1 - \frac{1}{5})=\frac{8}{25}$。
(2)若小勇选择方案一,设付款金额为$X$元,则$X$可能的取值为$300,400,500$。
则$P(X = 300)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$,$P(X = 400)=\frac{C_{3}^{1}C_{3}^{1}}{C_{6}^{2}}=\frac{3}{5}$,$P(X = 500)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$。
故$X$的分布列为
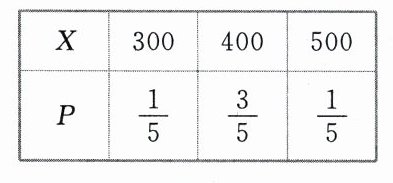
$\therefore E(X)=300\times\frac{1}{5}+400\times\frac{3}{5}+500\times\frac{1}{5}=400$(元)。
若小勇选择方案二,设摸到红球的个数为$Y$,付款金额为$Z$元,则$Z = 500 - 80Y$。
由已知,可得$Y\sim B(2,\frac{1}{2})$,故$E(Y)=2\times\frac{1}{2}=1$。
$\therefore E(Z)=E(500 - 80Y)=500 - 80E(Y)=500 - 80 = 420$(元)。
由上知$E(X)<E(Z)$,故小勇选择方案一更划算。
解析:
(1)由题意,设顾客享受到6折优惠为事件$A$,则$P(A)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$。
$\therefore$小方、小红两人其中有一人享受6折优惠的概率为
$P = C_{2}^{1}\cdot P(A)\cdot[1 - P(A)]=2\times\frac{1}{5}\times(1 - \frac{1}{5})=\frac{8}{25}$。
(2)若小勇选择方案一,设付款金额为$X$元,则$X$可能的取值为$300,400,500$。
则$P(X = 300)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$,$P(X = 400)=\frac{C_{3}^{1}C_{3}^{1}}{C_{6}^{2}}=\frac{3}{5}$,$P(X = 500)=\frac{C_{3}^{2}}{C_{6}^{2}}=\frac{1}{5}$。
故$X$的分布列为

$\therefore E(X)=300\times\frac{1}{5}+400\times\frac{3}{5}+500\times\frac{1}{5}=400$(元)。
若小勇选择方案二,设摸到红球的个数为$Y$,付款金额为$Z$元,则$Z = 500 - 80Y$。
由已知,可得$Y\sim B(2,\frac{1}{2})$,故$E(Y)=2\times\frac{1}{2}=1$。
$\therefore E(Z)=E(500 - 80Y)=500 - 80E(Y)=500 - 80 = 420$(元)。
由上知$E(X)<E(Z)$,故小勇选择方案一更划算。
查看更多完整答案,请扫码查看


