2025年万唯中考大小卷九年级数学全一册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷九年级数学全一册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
18. ( 8 分) 某店有一种丝绸制成的丝巾,每条成本 50 元,出于营销考虑,要求每条丝巾的售价不低于 60 元且不高于 110 元,一段时间后发现,每周的销售数量 y( 件) 与售价 x( 元/件) 满足一次函数关系,部分数据如下表所示:
|售价 x( 元/件)|70|90|100|
| ---- | ---- | ---- | ---- |
|每周销售数量 y( 件)|80|40|20|
( 1) 求 y 与 x 之间的函数表达式;
( 2) 将该丝巾售价定为多少元/件时,可使每周销售该丝巾所获利润 w 最大? 最大利润是多少?
|售价 x( 元/件)|70|90|100|
| ---- | ---- | ---- | ---- |
|每周销售数量 y( 件)|80|40|20|
( 1) 求 y 与 x 之间的函数表达式;
( 2) 将该丝巾售价定为多少元/件时,可使每周销售该丝巾所获利润 w 最大? 最大利润是多少?
答案:
解:
(1)$y$与$x$之间的函数表达式为$y = -2x + 220$;(4分)
(2)将该丝巾售价定为80元/件时,可使每周销售该丝巾所获利润最大,最大利润是1800元。(8分)
(1)$y$与$x$之间的函数表达式为$y = -2x + 220$;(4分)
(2)将该丝巾售价定为80元/件时,可使每周销售该丝巾所获利润最大,最大利润是1800元。(8分)
19. ( 教材 P49 第 6 题改编) ( 10 分) 如图,直线 $y = k_{1}x - 2$ 与双曲线 $y = \frac{k_{2}}{x}$ 交于 $A,B$ 两点,直线 $AB$ 与 x 轴交于点 $C$,与 y 轴交于点 $D$, $\angle OCD = 45^{\circ}, BD = 2\sqrt{2}$.
( 1) 求 $k_{1},k_{2}$ 的值;
( 2) 当 $k_{1}x - 2\leq\frac{k_{2}}{x}$ 时,结合图象求 x 的取值范围.

( 1) 求 $k_{1},k_{2}$ 的值;
( 2) 当 $k_{1}x - 2\leq\frac{k_{2}}{x}$ 时,结合图象求 x 的取值范围.

答案:
解:
(1)如解图,过点$B$作$BG\perp y$轴于点$G$。 $\because\angle OCD = 45^{\circ}$, $\therefore\angle DBG=\angle OCD = 45^{\circ}$, $\therefore DG = BG=\frac{BD}{\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2}} = 2$。(2分) 由$y = k_{1}x - 2$知$D(0,-2)$,即$OD = 2$, $\therefore OG = 4$,$\therefore B(-2,-4)$。 将$B(-2,-4)$分别代入$y = k_{1}x - 2$与$y=\frac{k_{2}}{x}$, 得$-4 = k_{1}\cdot(-2)-2$,$-4=\frac{k_{2}}{-2}$, 解得$k_{1}=1$,$k_{2}=8$;(5分)
(2)由
(1)得两函数的表达式分别为$y = x - 2$和$y=\frac{8}{x}$, 令$x - 2=\frac{8}{x}$,解得$x_{1}=-2$,$x_{2}=4$, $\therefore A(4,2)$,$B(-2,-4)$, $\therefore$由图象知,当$k_{1}x - 2\leq\frac{k_{2}}{x}$时,$x$的取值范围为$x\leq -2$或$0 < x\leq4$。(10分)
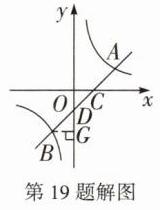
解:
(1)如解图,过点$B$作$BG\perp y$轴于点$G$。 $\because\angle OCD = 45^{\circ}$, $\therefore\angle DBG=\angle OCD = 45^{\circ}$, $\therefore DG = BG=\frac{BD}{\sqrt{2}}=\frac{2\sqrt{2}}{\sqrt{2}} = 2$。(2分) 由$y = k_{1}x - 2$知$D(0,-2)$,即$OD = 2$, $\therefore OG = 4$,$\therefore B(-2,-4)$。 将$B(-2,-4)$分别代入$y = k_{1}x - 2$与$y=\frac{k_{2}}{x}$, 得$-4 = k_{1}\cdot(-2)-2$,$-4=\frac{k_{2}}{-2}$, 解得$k_{1}=1$,$k_{2}=8$;(5分)
(2)由
(1)得两函数的表达式分别为$y = x - 2$和$y=\frac{8}{x}$, 令$x - 2=\frac{8}{x}$,解得$x_{1}=-2$,$x_{2}=4$, $\therefore A(4,2)$,$B(-2,-4)$, $\therefore$由图象知,当$k_{1}x - 2\leq\frac{k_{2}}{x}$时,$x$的取值范围为$x\leq -2$或$0 < x\leq4$。(10分)

查看更多完整答案,请扫码查看


