2025年万唯中考大小卷九年级数学全一册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷九年级数学全一册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (12分)如图,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,$D$为$AB$的中点,$P$是边$AC$上一动点,连接$BP$,$CD$相交于点$E$,连接$PD$.
(1)若$P$为$AC$的中点,判断$BE$与$PE$的数量关系,并说明理由;
(2)若$PD// BC$,$\tan\angle ADP = 2$,$BC = 2$,求$DE$的长;
(3)若$PD\perp AB$,$DE = 2CE$,求$\sin A$的值.

(1)若$P$为$AC$的中点,判断$BE$与$PE$的数量关系,并说明理由;
(2)若$PD// BC$,$\tan\angle ADP = 2$,$BC = 2$,求$DE$的长;
(3)若$PD\perp AB$,$DE = 2CE$,求$\sin A$的值.

答案:
解:
(1) $BE = 2PE$,理由如下: $\because P$ 为 $AC$ 的中点,$D$ 为 $AB$ 的中点, $\therefore DP$ 是 $\triangle ABC$ 的中位线, $\therefore DP=\frac{1}{2}BC$,$DP// BC$, $\therefore \triangle PDE\sim\triangle BCE$,$\frac{PE}{BE}=\frac{PD}{BC}=\frac{1}{2}$, $\therefore BE = 2PE$; (4分)
(2) $\because PD// BC$,$\therefore \angle ABC=\angle ADP$. $\because \tan\angle ADP = 2$, $\therefore \tan\angle ABC=\tan\angle ADP = 2$. 在 $Rt\triangle ABC$ 中,$\because BC = 2$, $\therefore AC = BC\cdot\tan\angle ABC = 4$, $\therefore AB=\sqrt{BC^{2}+AC^{2}}=2\sqrt{5}$. $\because D$ 是 $AB$ 的中点,$PD// BC$, $\therefore PD$ 是 $\triangle ABC$ 的中位线,$CD=\frac{1}{2}AB=\sqrt{5}$, $\triangle PDE\sim\triangle BCE$, $\therefore PD=\frac{1}{2}BC$,$\frac{DE}{CE}=\frac{PD}{BC}=\frac{1}{2}$, $\therefore DE=\frac{1}{3}CD=\frac{\sqrt{5}}{3}$; (8分)
(3) 如解图,过点 $B$ 作 $BF// AC$,交 $CD$ 的延长线于点 $F$, $\therefore \triangle ACD\sim\triangle BFD$, $\therefore \frac{BD}{AD}=\frac{FD}{CD}=\frac{BF}{AC}$. $\because BD = DA$, $\therefore FD = CD$,$BF = AC$. $\because DE = 2CE$, $\therefore FD = CD = 3CE$,$\therefore EF = 5CE$. $\because BF// AC$,$\therefore \triangle BEF\sim\triangle PEC$, $\therefore \frac{PC}{AC}=\frac{PC}{BF}=\frac{EC}{EF}=\frac{1}{5}$. (10分) 设 $PC = k$,则 $AC = 5k$,$PA = 4k$, $\because PD\perp AB$,$D$ 是 $AB$ 的中点, $\therefore PB = PA = 4k$, $\therefore BC=\sqrt{(4k)^{2}-k^{2}}=\sqrt{15}k$. $\because AC = 5k$, $\therefore AB=\sqrt{(\sqrt{15}k)^{2}+(5k)^{2}}=2\sqrt{10}k$, (11分) $\therefore \sin A=\frac{BC}{AB}=\frac{\sqrt{15}k}{2\sqrt{10}k}=\frac{\sqrt{6}}{4}$. (12分)
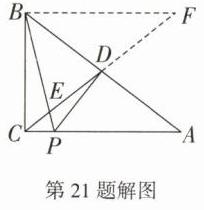
解:
(1) $BE = 2PE$,理由如下: $\because P$ 为 $AC$ 的中点,$D$ 为 $AB$ 的中点, $\therefore DP$ 是 $\triangle ABC$ 的中位线, $\therefore DP=\frac{1}{2}BC$,$DP// BC$, $\therefore \triangle PDE\sim\triangle BCE$,$\frac{PE}{BE}=\frac{PD}{BC}=\frac{1}{2}$, $\therefore BE = 2PE$; (4分)
(2) $\because PD// BC$,$\therefore \angle ABC=\angle ADP$. $\because \tan\angle ADP = 2$, $\therefore \tan\angle ABC=\tan\angle ADP = 2$. 在 $Rt\triangle ABC$ 中,$\because BC = 2$, $\therefore AC = BC\cdot\tan\angle ABC = 4$, $\therefore AB=\sqrt{BC^{2}+AC^{2}}=2\sqrt{5}$. $\because D$ 是 $AB$ 的中点,$PD// BC$, $\therefore PD$ 是 $\triangle ABC$ 的中位线,$CD=\frac{1}{2}AB=\sqrt{5}$, $\triangle PDE\sim\triangle BCE$, $\therefore PD=\frac{1}{2}BC$,$\frac{DE}{CE}=\frac{PD}{BC}=\frac{1}{2}$, $\therefore DE=\frac{1}{3}CD=\frac{\sqrt{5}}{3}$; (8分)
(3) 如解图,过点 $B$ 作 $BF// AC$,交 $CD$ 的延长线于点 $F$, $\therefore \triangle ACD\sim\triangle BFD$, $\therefore \frac{BD}{AD}=\frac{FD}{CD}=\frac{BF}{AC}$. $\because BD = DA$, $\therefore FD = CD$,$BF = AC$. $\because DE = 2CE$, $\therefore FD = CD = 3CE$,$\therefore EF = 5CE$. $\because BF// AC$,$\therefore \triangle BEF\sim\triangle PEC$, $\therefore \frac{PC}{AC}=\frac{PC}{BF}=\frac{EC}{EF}=\frac{1}{5}$. (10分) 设 $PC = k$,则 $AC = 5k$,$PA = 4k$, $\because PD\perp AB$,$D$ 是 $AB$ 的中点, $\therefore PB = PA = 4k$, $\therefore BC=\sqrt{(4k)^{2}-k^{2}}=\sqrt{15}k$. $\because AC = 5k$, $\therefore AB=\sqrt{(\sqrt{15}k)^{2}+(5k)^{2}}=2\sqrt{10}k$, (11分) $\therefore \sin A=\frac{BC}{AB}=\frac{\sqrt{15}k}{2\sqrt{10}k}=\frac{\sqrt{6}}{4}$. (12分)

查看更多完整答案,请扫码查看


