《2025年万唯中考大小卷九年级数学全一册沪科版》

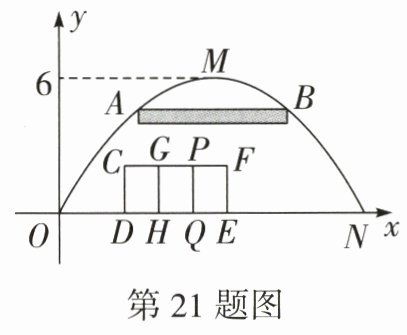
21. (中考新考法·综合与实践——课题实践活动)(12 分)毛竹工艺品远销全球,安徽广德就是中国十大毛竹之乡之一. 某度假村利用毛竹为原材料做成一个抛物线型的凯旋门,按照如图所示的方式建立平面直角坐标系,已知其跨度 ON 为 16 米,且最高点距地面 6 米.
(1)求抛物线对应的函数表达式;
(2)凯旋门的上方悬挂一个长为 6 米,宽为 0.5 米的牌匾,牌匾的上沿 $AB// x$ 轴,点 A,B 在抛物线上. 一辆高为 4.6 米的厢式货车沿大门中间行驶,能否顺利通过? 请说明理由;
(3)为了便于清理凯旋门,环卫师傅用 16 米的材料做了一个 型的脚手架,其中矩形 CDEF 的边 DE 不用材料,立杆 GH,PQ 与 CD 平行且相等.
①如何设计脚手架,使矩形 CDEF 的面积 S(平方米)最大?
②当矩形 CDEF 的面积最大时,左右移动脚手架,求点 E 的横坐标的取值范围.

答案： 解：
(1) 抛物线对应的函数表达式为 $y = -\frac{3}{32}(x - 8)^{2}+6$；（3分）
(2) 能顺利通过。 理由如下：$\because AB = 6$ 米，
∴ 点 $A$ 的横坐标为5。 当 $x = 5$ 时，$y = -\frac{3}{32}\times(5 - 8)^{2}+6 = 5\frac{5}{32}$， $5\frac{5}{32}-0.5\approx4.66$（米）， $\because 4.6 ＜ 4.66$，
∴ 能顺利通过；（6分）
(3) ①设 $EF = n$ 米，则 $CF=(16 - 4n)$ 米， $\therefore S = n(16 - 4n)=-4(n - 2)^{2}+16$。 $\because -4 ＜ 0$，
∴ 当 $n = 2$ 时，$S$ 取得最大值，最大值为16， 此时 $CF = 16 - 4\times2 = 8$（米）， 即当 $CD = 2$ 米，$CF = 8$ 米时，矩形 $CDEF$ 的面积最大；（9分） ②把 $y = 2$ 代入 $y = -\frac{3}{32}(x - 8)^{2}+6$， 得 $-\frac{3}{32}(x - 8)^{2}+6 = 2$， 解得 $x_{1}=8+\frac{8\sqrt{6}}{3}$，$x_{2}=8-\frac{8\sqrt{6}}{3}$。 当 $x = 8-\frac{8\sqrt{6}}{3}$ 时，点 $E$ 的横坐标为 $8-\frac{8\sqrt{6}}{3}+8 = 16-\frac{8\sqrt{6}}{3}$，
∴ 点 $E$ 的横坐标的取值范围是 $16-\frac{8\sqrt{6}}{3}\leq x_{E}\leq8+\frac{8\sqrt{6}}{3}$。（12分）