2025年万唯中考大小卷九年级数学全一册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷九年级数学全一册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
主题情境 鱼苗培育 张叔叔承包了一块水产养殖区域,想要培育不同种类的鱼,并做了一些辅助工作. 请完成第 17~18 题.
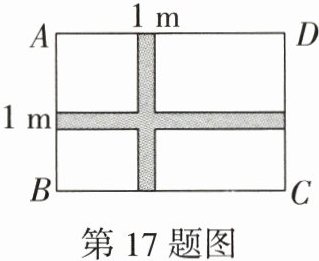
17. (8 分)张叔叔用长为 36 m 的围网在水库围一块矩形水面,为方便投放不同种类鱼苗,围成的水面还需分为四部分区域(划分区域围网也包含在 36 m 的围网中,即四部分区域的周长即为围网长度),中间是两条宽为 1 m 的通道,设$AB = x$ m,矩形$ABCD$的面积为$S$ m².
(1)求$S$关于$x$的函数表达式,并写$x$的取值范围.
(2)求$S$的最大值.
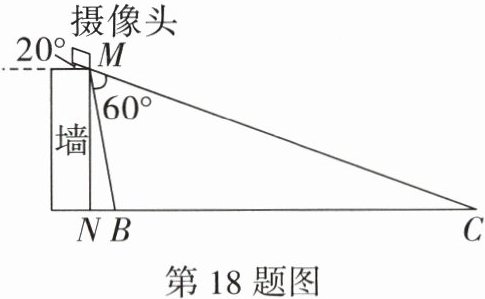
18. (10 分)鱼苗的培育,需要养殖者时刻关注鱼苗的成长和环境的变化,给予及时的对应的处理方法才能成功培育. 为了方便观测养殖区域情况,张叔叔在墙壁上安装了一个摄像头. 如图,摄像头$M$到水平地面的距离为$MN$,养殖区域的长度$BC = 8.4$ m,$N$,$B$,$C$三点在同一水平线上. 已知摄像头的可视角度$\angle CMB = 60^{\circ}$,当摄像头与水平面的夹角为$20^{\circ}$,即$\angle C = 20^{\circ}$时,恰好可以检测到$BC$区域,已知点$M$,$N$,$B$,$C$在同一平面内,求摄像头安装的高度$MN$.(结果精确到 0.01,参考数据:$\sin 10^{\circ}\approx0.17$,$\cos 10^{\circ}\approx0.98$,$\tan 10^{\circ}\approx0.18$,$\sin 70^{\circ}\approx0.94$,$\cos 70^{\circ}\approx0.34$,$\tan 70^{\circ}\approx2.75$)
17. (8 分)张叔叔用长为 36 m 的围网在水库围一块矩形水面,为方便投放不同种类鱼苗,围成的水面还需分为四部分区域(划分区域围网也包含在 36 m 的围网中,即四部分区域的周长即为围网长度),中间是两条宽为 1 m 的通道,设$AB = x$ m,矩形$ABCD$的面积为$S$ m².
(1)求$S$关于$x$的函数表达式,并写$x$的取值范围.
(2)求$S$的最大值.

18. (10 分)鱼苗的培育,需要养殖者时刻关注鱼苗的成长和环境的变化,给予及时的对应的处理方法才能成功培育. 为了方便观测养殖区域情况,张叔叔在墙壁上安装了一个摄像头. 如图,摄像头$M$到水平地面的距离为$MN$,养殖区域的长度$BC = 8.4$ m,$N$,$B$,$C$三点在同一水平线上. 已知摄像头的可视角度$\angle CMB = 60^{\circ}$,当摄像头与水平面的夹角为$20^{\circ}$,即$\angle C = 20^{\circ}$时,恰好可以检测到$BC$区域,已知点$M$,$N$,$B$,$C$在同一平面内,求摄像头安装的高度$MN$.(结果精确到 0.01,参考数据:$\sin 10^{\circ}\approx0.17$,$\cos 10^{\circ}\approx0.98$,$\tan 10^{\circ}\approx0.18$,$\sin 70^{\circ}\approx0.94$,$\cos 70^{\circ}\approx0.34$,$\tan 70^{\circ}\approx2.75$)

答案:
解:
(1) $S = x(10 - x)=-x^{2}+10x(1\lt x\lt9)$;……(4分)
(2) 当$x = 5$时,$S$有最大值,最大值为25。……(8分)
@@解:根据题意可知$\angle MNC = 90^{\circ}$,$\angle CMB = 60^{\circ}$,$\angle C = 20^{\circ}$, $\therefore \angle NMC = 90^{\circ}-20^{\circ}=70^{\circ}$,$\tan70^{\circ}=\frac{NC}{MN}$, $\therefore NC=\tan70^{\circ}\cdot MN$。……(3分) 在$Rt\triangle NMB$中,$\angle NMB = 70^{\circ}-60^{\circ}=10^{\circ}$, $\therefore NB=\tan10^{\circ}\cdot MN$,……(6分) $\therefore BC = NC - NB=\tan70^{\circ}\cdot MN-\tan10^{\circ}\cdot MN = 8.4$, 即$2.75MN - 0.18MN = 8.4$,解得$MN\approx3.27$。 $\therefore$摄像头安装的高度约为3.27 m。…(10分)
(1) $S = x(10 - x)=-x^{2}+10x(1\lt x\lt9)$;……(4分)
(2) 当$x = 5$时,$S$有最大值,最大值为25。……(8分)
@@解:根据题意可知$\angle MNC = 90^{\circ}$,$\angle CMB = 60^{\circ}$,$\angle C = 20^{\circ}$, $\therefore \angle NMC = 90^{\circ}-20^{\circ}=70^{\circ}$,$\tan70^{\circ}=\frac{NC}{MN}$, $\therefore NC=\tan70^{\circ}\cdot MN$。……(3分) 在$Rt\triangle NMB$中,$\angle NMB = 70^{\circ}-60^{\circ}=10^{\circ}$, $\therefore NB=\tan10^{\circ}\cdot MN$,……(6分) $\therefore BC = NC - NB=\tan70^{\circ}\cdot MN-\tan10^{\circ}\cdot MN = 8.4$, 即$2.75MN - 0.18MN = 8.4$,解得$MN\approx3.27$。 $\therefore$摄像头安装的高度约为3.27 m。…(10分)
查看更多完整答案,请扫码查看


