《2025年万唯中考大小卷九年级数学全一册沪科版》

22. （中考新考法·综合与实践——类比探究）（12 分）某数学兴趣小组在数学课外活动中，进行了如下研究：
【初步感知】
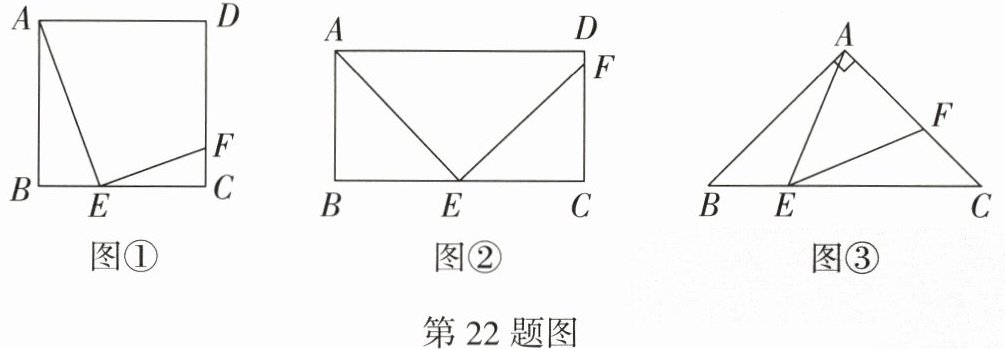
（1）如图①，在正方形$ABCD$中，$E$为$BC$边上一点，连接$AE$，过点$E$作$EF\perp AE$交$CD$于点$F$，则$\triangle ABE$与$\triangle ECF$_______（填“相似”或“不相似”）；
【类比探究】
（2）如图②，在矩形$ABCD$中，$E$为$BC$边的中点，连接$AE$，过点$E$作$EF\perp AE$交$CD$于点$F$，若$AB = 10.5$，$BC = 18$，求$CF$的长；
【拓展应用】
（3）如图③，在等腰直角$\triangle ABC$中，$\angle BAC = 90^{\circ}$，$AB = AC = 8\sqrt{2}$，$E$为$BC$边上一点（点$E$不与点$B$，$C$重合），连接$AE$，过点$E$作$\angle AEF = 45^{\circ}$交$AC$于点$F$，若$CF = 3\sqrt{2}$，求$BE$的长.

答案： 解：
(1) 相似；……（2分）
(2) $\because$四边形$ABCD$是矩形， $\therefore \angle B=\angle C = 90^{\circ}$， $\therefore \angle BAE+\angle BEA = 90^{\circ}$。 $\because EF\perp AE$， $\therefore \angle AEF = 90^{\circ}$， $\therefore \angle CEF+\angle BEA = 90^{\circ}$， $\therefore \angle BAE=\angle CEF$， $\therefore \triangle ABE\sim\triangle ECF$， $\therefore \frac{AB}{EC}=\frac{BE}{CF}$。 $\because E$为$BC$边的中点， $\therefore BE = EC = 9$， $\therefore \frac{10.5}{9}=\frac{9}{CF}$，解得$CF=\frac{54}{7}$；……（7分）
(3) 根据题意，得$\angle B=\angle C = 45^{\circ}$， $\therefore \angle AEB+\angle BAE = 180^{\circ}-\angle B = 135^{\circ}$。 $\because \angle AEF = 45^{\circ}$， $\therefore \angle AEB+\angle CEF = 180^{\circ}-\angle AEF = 135^{\circ}$， $\therefore \angle BAE=\angle CEF$， $\therefore \triangle ABE\sim\triangle ECF$， $\therefore \frac{AB}{EC}=\frac{BE}{CF}$。 $\because AB = AC = 8\sqrt{2}$，$\therefore BC = 16$。 设$BE = x$，则$CE = 16 - x$， $\therefore \frac{8\sqrt{2}}{16 - x}=\frac{x}{3\sqrt{2}}$，即$x^{2}-16x + 48 = 0$，解得$x = 4$或$x = 12$， $\therefore BE$的长为4或12。……（12分）