2025年万唯中考大小卷九年级数学全一册沪科版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年万唯中考大小卷九年级数学全一册沪科版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
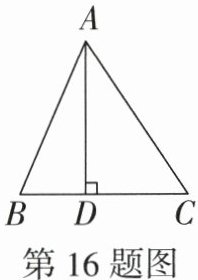
16. (6分)如图,在$\triangle ABC$中,$AD$是$BC$边上的高,已知$AD = 12$,$BC = 13$,$\tan C=\frac{3}{2}$.
(1)求线段$BD$的长;
(2)求$\cos B$的值.
(1)求线段$BD$的长;
(2)求$\cos B$的值.

答案:
解:
(1) $BD = 5$;(3分)
(2) $\cos B=\frac{5}{13}$. (6分)
(1) $BD = 5$;(3分)
(2) $\cos B=\frac{5}{13}$. (6分)
17. (8分)如图,将矩形纸片$ABCD$沿着$AE$折叠,使点$D$恰好落在$BC$边上的点$F$处,已知$AB:AD = 3:4$.
(1)求$\tan\angle FEC$的值;
(2)若$AB = 30$,求$CF$的长.

(1)求$\tan\angle FEC$的值;
(2)若$AB = 30$,求$CF$的长.

答案:
解:
(1) $\because AB:AD = 3:4$, $\therefore$ 设 $AB = 3x$,则 $AD = 4x$. 根据折叠的性质,可得 $AF = AD = 4x$,$\angle AFE=\angle D = 90^{\circ}$, $\therefore BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{7}x$. (3分) $\because \angle EFC+\angle FEC = 90^{\circ}$,$\angle EFC+\angle AFB = 90^{\circ}$, $\therefore \angle FEC=\angle AFB$, $\therefore \tan\angle FEC=\tan\angle AFB=\frac{AB}{BF}=\frac{3x}{\sqrt{7}x}=\frac{3\sqrt{7}}{7}$; (6分)
(2) $\because AB = 30$,$\therefore x = 10$, $\therefore BC = AD = 4x = 40$,$BF=\sqrt{7}x = 10\sqrt{7}$, $\therefore CF = BC - BF = 40 - 10\sqrt{7}$. (8分)
(1) $\because AB:AD = 3:4$, $\therefore$ 设 $AB = 3x$,则 $AD = 4x$. 根据折叠的性质,可得 $AF = AD = 4x$,$\angle AFE=\angle D = 90^{\circ}$, $\therefore BF=\sqrt{AF^{2}-AB^{2}}=\sqrt{7}x$. (3分) $\because \angle EFC+\angle FEC = 90^{\circ}$,$\angle EFC+\angle AFB = 90^{\circ}$, $\therefore \angle FEC=\angle AFB$, $\therefore \tan\angle FEC=\tan\angle AFB=\frac{AB}{BF}=\frac{3x}{\sqrt{7}x}=\frac{3\sqrt{7}}{7}$; (6分)
(2) $\because AB = 30$,$\therefore x = 10$, $\therefore BC = AD = 4x = 40$,$BF=\sqrt{7}x = 10\sqrt{7}$, $\therefore CF = BC - BF = 40 - 10\sqrt{7}$. (8分)
主题情境 “古逍遥津”测量实践 “曹操平定汉中地,张辽威震逍遥津”,小明周末前往“古逍遥津”游玩,进行了一场“古逍遥津”测量之旅. 请完成第18~19题.
18. (8分)抵达公园后,小明先对图①所示公园门口匾额的悬挂高度进行了测量. 图②是匾额截面示意图,在$D$处用测量仪测得匾额上端$C$处的仰角为$\alpha = 45^{\circ}$,走近门口在$E$处测得匾额底端$B$处的仰角是$\gamma = 53^{\circ}$,已知$D$,$E$两点间的距离为$2.3$m,匾额的宽度为$1.2$m,且其与悬挂墙面的夹角为$\beta = 37^{\circ}$,测量仪高度$DD' = EE' = 1$m($A$,$B$,$C$,$D$,$D'$,$E$,$E'$,$M$均在同一平面内).
(1)请你根据上面给出的数据,计算匾额顶端$C$到竖直墙面$AM$的水平距离;
(2)请求出匾额底端$B$到地面$AD$的高度.(结果精确到$0.01$m,参考数据:$\sin37^{\circ}\approx0.60$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$)

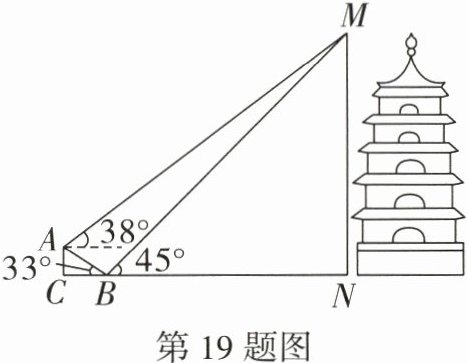
19. (10分)如图,在对古逍遥津公园中的逍遥阁高度进行测量时,小明先站在渡津桥上点$A$处,测得阁顶$M$的仰角为$38^{\circ}$,沿桥面$AB$步行$4$m后,在点$B$处测得阁顶$M$的仰角为$45^{\circ}$,已知$\angle ABC = 33^{\circ}$,点$C$,$B$,$N$在同一直线上,求逍遥阁的高度$MN$.(结果精确到整数,参考数据:$\sin33^{\circ}\approx0.54$,$\cos33^{\circ}\approx0.84$,$\tan33^{\circ}\approx0.65$,$\sin38^{\circ}\approx0.62$,$\cos38^{\circ}\approx0.79$,$\tan38^{\circ}\approx0.78$)
18. (8分)抵达公园后,小明先对图①所示公园门口匾额的悬挂高度进行了测量. 图②是匾额截面示意图,在$D$处用测量仪测得匾额上端$C$处的仰角为$\alpha = 45^{\circ}$,走近门口在$E$处测得匾额底端$B$处的仰角是$\gamma = 53^{\circ}$,已知$D$,$E$两点间的距离为$2.3$m,匾额的宽度为$1.2$m,且其与悬挂墙面的夹角为$\beta = 37^{\circ}$,测量仪高度$DD' = EE' = 1$m($A$,$B$,$C$,$D$,$D'$,$E$,$E'$,$M$均在同一平面内).
(1)请你根据上面给出的数据,计算匾额顶端$C$到竖直墙面$AM$的水平距离;
(2)请求出匾额底端$B$到地面$AD$的高度.(结果精确到$0.01$m,参考数据:$\sin37^{\circ}\approx0.60$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$)

19. (10分)如图,在对古逍遥津公园中的逍遥阁高度进行测量时,小明先站在渡津桥上点$A$处,测得阁顶$M$的仰角为$38^{\circ}$,沿桥面$AB$步行$4$m后,在点$B$处测得阁顶$M$的仰角为$45^{\circ}$,已知$\angle ABC = 33^{\circ}$,点$C$,$B$,$N$在同一直线上,求逍遥阁的高度$MN$.(结果精确到整数,参考数据:$\sin33^{\circ}\approx0.54$,$\cos33^{\circ}\approx0.84$,$\tan33^{\circ}\approx0.65$,$\sin38^{\circ}\approx0.62$,$\cos38^{\circ}\approx0.79$,$\tan38^{\circ}\approx0.78$)

答案:
解:
(1) 如解图,过点 $C$ 作 $CQ\perp AM$ 于点 $Q$, 在 $Rt\triangle CBQ$ 中,$BC = 1.2$ m,$\beta = 37^{\circ}$, $\therefore CQ = BC\cdot\sin 37^{\circ}\approx1.2\times0.60 = 0.72$(m), 答:匾额顶端 $C$ 到竖直墙面 $AM$ 的水平距离约为 0.72 m; (4分)
(2) 如解图,延长 $DD'$,$QC$ 交于点 $P$,设 $A'B = x$ m, 在 $Rt\triangle A'BE'$ 中,$\gamma = 53^{\circ}$,$\therefore \angle A'BE' = 37^{\circ}$, $\therefore A'E' = A'B\cdot\tan 37^{\circ}\approx0.75x$ m, $\therefore A'D' = D'E'+A'E'=(2.3 + 0.75x)$ m. 在 $Rt\triangle CPD'$ 中,$\angle PCD'=\alpha = 45^{\circ}$, 由
(1)知 $BQ = BC\cdot\cos 37^{\circ}\approx0.96$(m), $\therefore PC = PD' = A'Q=(x + 0.96)$ m. $\because PQ = A'D'$, $\therefore x + 0.96+0.72 = 0.75x + 2.3$, 解得 $x = 2.48$, $\therefore AB = AA'+A'B = 1 + 2.48 = 3.48$(m). 答:匾额底端 $B$ 到地面 $AD$ 的高度约为 3.48 m. (8分)
@@解:如解图,过点 $A$ 作 $AD\perp MN$ 于点 $D$, 根据题意,得 $AB = 4$ m,$MN\perp CN$, $\because \angle MBN = 45^{\circ}$,$\therefore BN = MN$. $\because \angle ABC = 33^{\circ}$, $\therefore BC = AB\cdot\cos 33^{\circ}$,$AC = DN = AB\cdot\sin 33^{\circ}$, $\therefore AD = CN = BC + BN = AB\cdot\cos 33^{\circ}+MN$, $MD = MN - DN = MN - AB\cdot\sin 33^{\circ}$. $\because \angle MAD = 38^{\circ}$, $\therefore \tan 38^{\circ}=\frac{MD}{AD}=\frac{MN - AB\cdot\sin 33^{\circ}}{MN + AB\cdot\cos 33^{\circ}}$, 解得 $MN\approx22$ m. 答:逍遥阁的高度约为 22 m. (10分)
解:
(1) 如解图,过点 $C$ 作 $CQ\perp AM$ 于点 $Q$, 在 $Rt\triangle CBQ$ 中,$BC = 1.2$ m,$\beta = 37^{\circ}$, $\therefore CQ = BC\cdot\sin 37^{\circ}\approx1.2\times0.60 = 0.72$(m), 答:匾额顶端 $C$ 到竖直墙面 $AM$ 的水平距离约为 0.72 m; (4分)
(2) 如解图,延长 $DD'$,$QC$ 交于点 $P$,设 $A'B = x$ m, 在 $Rt\triangle A'BE'$ 中,$\gamma = 53^{\circ}$,$\therefore \angle A'BE' = 37^{\circ}$, $\therefore A'E' = A'B\cdot\tan 37^{\circ}\approx0.75x$ m, $\therefore A'D' = D'E'+A'E'=(2.3 + 0.75x)$ m. 在 $Rt\triangle CPD'$ 中,$\angle PCD'=\alpha = 45^{\circ}$, 由
(1)知 $BQ = BC\cdot\cos 37^{\circ}\approx0.96$(m), $\therefore PC = PD' = A'Q=(x + 0.96)$ m. $\because PQ = A'D'$, $\therefore x + 0.96+0.72 = 0.75x + 2.3$, 解得 $x = 2.48$, $\therefore AB = AA'+A'B = 1 + 2.48 = 3.48$(m). 答:匾额底端 $B$ 到地面 $AD$ 的高度约为 3.48 m. (8分)

@@解:如解图,过点 $A$ 作 $AD\perp MN$ 于点 $D$, 根据题意,得 $AB = 4$ m,$MN\perp CN$, $\because \angle MBN = 45^{\circ}$,$\therefore BN = MN$. $\because \angle ABC = 33^{\circ}$, $\therefore BC = AB\cdot\cos 33^{\circ}$,$AC = DN = AB\cdot\sin 33^{\circ}$, $\therefore AD = CN = BC + BN = AB\cdot\cos 33^{\circ}+MN$, $MD = MN - DN = MN - AB\cdot\sin 33^{\circ}$. $\because \angle MAD = 38^{\circ}$, $\therefore \tan 38^{\circ}=\frac{MD}{AD}=\frac{MN - AB\cdot\sin 33^{\circ}}{MN + AB\cdot\cos 33^{\circ}}$, 解得 $MN\approx22$ m. 答:逍遥阁的高度约为 22 m. (10分)

查看更多完整答案,请扫码查看


