《2025年万唯中考大小卷九年级数学全一册沪科版》

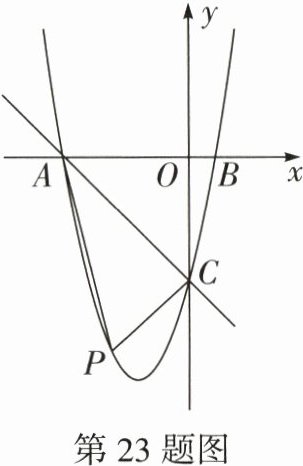
23. （12 分）如图，抛物线$y = x^{2}+4x - 5$与$x$轴交于$A$，$B$两点（点$A$在点$B$左侧），与$y$轴交于点$C$.
（1）求$A$，$B$，$C$三点的坐标；
（2）点$P$为直线$AC$下方抛物线上一点，连接$PA$，$PC$，求$\triangle PAC$面积的最大值；
（3）点$E$是抛物线上一动点，当$\angle EAC = 15^{\circ}$时，求直线$AE$对应的函数表达式.

答案：
解：
(1) 点$A$的坐标为$(-5,0)$，点$B$的坐标为$(1,0)$， 点$C$的坐标为$(0,-5)$；……（3分）
(2) 当$m =-\frac{5}{2}$时，$\triangle PAC$的面积最大，最大值为$\frac{125}{8}$；……（7分）
(3) $\because A(-5,0)$，$C(0,-5)$，$\therefore OA = OC = 5$， $\therefore \triangle OAC$是等腰直角三角形， $\therefore \angle OAC=\angle OCA = 45^{\circ}$。 如解图，当点$E_1$在直线$AC$上方时，直线$AE_1$交$y$轴于点$F_1$， $\because \angle CAE_1 = 15^{\circ}$，$\therefore \angle OAF_1=\angle OAC-\angle CAF_1 = 45^{\circ}-15^{\circ}=30^{\circ}$， $\therefore OF_1=\tan30^{\circ}\cdot OA=\frac{5\sqrt{3}}{3}$， $\therefore$点$F_1(0,-\frac{5\sqrt{3}}{3})$。 设直线$AE_1$对应的函数表达式为$y = k_1x + b_1(k_1\neq0)$， $\because$直线$AE_1$经过$A(-5,0)$，$F_1(0,-\frac{5\sqrt{3}}{3})$， $\therefore \begin{cases}-5k_1 + b_1 = 0\\b_1=-\frac{5\sqrt{3}}{3}\end{cases}$，解得$\begin{cases}k_1=-\frac{\sqrt{3}}{3}\\b_1=-\frac{5\sqrt{3}}{3}\end{cases}$， $\therefore y =-\frac{\sqrt{3}}{3}x-\frac{5\sqrt{3}}{3}$；……（10分） 如解图，当点$E_2$在直线$AC$下方时，直线$AE_2$交$y$轴于点$F_2$， $\because \angle CAE_2 = 15^{\circ}$， $\therefore \angle OAF_2=\angle OAC+\angle CAF_2 = 45^{\circ}+15^{\circ}=60^{\circ}$， $\therefore OF_2=\tan60^{\circ}\cdot OA = 5\sqrt{3}$， $\therefore$点$F_2(0,-5\sqrt{3})$。 设直线$AE_2$对应的函数表达式为$y = k_2x + b_2(k_2\neq0)$， $\because$直线$AE_2$经过$A(-5,0)$，$F_2(0,-5\sqrt{3})$， $\therefore \begin{cases}-5k_2 + b_2 = 0\\b_2=-5\sqrt{3}\end{cases}$，解得$\begin{cases}k_2=-\sqrt{3}\\b_2=-5\sqrt{3}\end{cases}$， $\therefore y =-\sqrt{3}x - 5\sqrt{3}$。 综上所述，直线$AE$对应的函数表达式为$y =-\frac{\sqrt{3}}{3}x-\frac{5\sqrt{3}}{3}$或$y =-\sqrt{3}x - 5\sqrt{3}$。……（12分）