第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
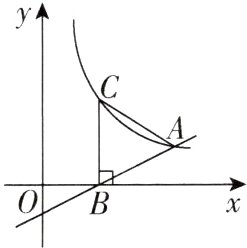
8[2024江苏盐城三模]如图,直线$y = \frac{1}{2}x - 1$与x轴交于点B,与双曲线$y = \frac{k}{x}(x > 0)$交于点A,过点B作x轴的垂线,与双曲线$y = \frac{k}{x}(x > 0)$交于点C,且$AB = AC$,则k的值为________.

答案:
4【解析】
∵直线$y = \frac{1}{2}x - 1$与$x$轴交于点$B$,
∴令$y = 0$,解得$x = 2$,
∴点$B$的坐标为$(2,0)$。
又
∵过点$B$作$x$轴的垂线,与双曲线$y = \frac{k}{x}(x > 0)$交于点$C$,
∴点$C$的坐标为$(2,\frac{k}{2})$。
∵$AB = AC$,
∴点$A$在线段$BC$的垂直平分线上,
∴点$A$的纵坐标为$\frac{k}{4}$。
∵点$A$在双曲线$y = \frac{k}{x}(x > 0)$上,
∴$\frac{k}{4} = \frac{k}{x}$,
∴$x = 4$,
∴$A(4,\frac{k}{4})$。又
∵点$A(4,\frac{k}{4})$在直线$y = \frac{1}{2}x - 1$上,
∴$\frac{k}{4} = \frac{1}{2}×4 - 1$,解得$k = 4$。故答案为 4。
∵直线$y = \frac{1}{2}x - 1$与$x$轴交于点$B$,
∴令$y = 0$,解得$x = 2$,
∴点$B$的坐标为$(2,0)$。
又
∵过点$B$作$x$轴的垂线,与双曲线$y = \frac{k}{x}(x > 0)$交于点$C$,
∴点$C$的坐标为$(2,\frac{k}{2})$。
∵$AB = AC$,
∴点$A$在线段$BC$的垂直平分线上,
∴点$A$的纵坐标为$\frac{k}{4}$。
∵点$A$在双曲线$y = \frac{k}{x}(x > 0)$上,
∴$\frac{k}{4} = \frac{k}{x}$,
∴$x = 4$,
∴$A(4,\frac{k}{4})$。又
∵点$A(4,\frac{k}{4})$在直线$y = \frac{1}{2}x - 1$上,
∴$\frac{k}{4} = \frac{1}{2}×4 - 1$,解得$k = 4$。故答案为 4。
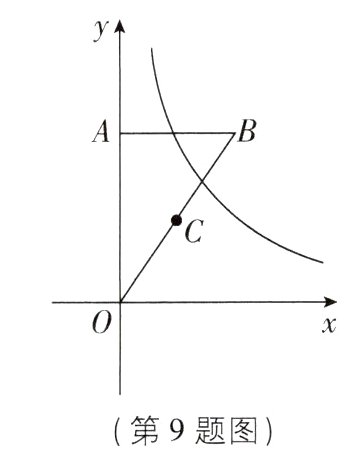
9[2023江苏苏州姑苏区期中]如图,在平面直角坐标系中,Rt$\triangle OAB$的一条边OA在y轴上,$OA = 4$,$AB = 3$,$\angle OAB = 90^{\circ}$. 将$\triangle OAB$向右平移,某一时刻,反比例函数$y = \frac{k}{x}(k \neq 0,x > 0)$的图像恰好经过点A和OB的中点C,则平移的长度是________.

答案:
$\frac{3}{2}$【解析】
∵$Rt\triangle OAB$的一条边$OA$在$y$轴上,$OA = 4$,$AB = 3$,
∴$A(0,4)$,$B(3,4)$,
∴$OB$的中点$C(\frac{3}{2},2)$。设$\triangle OAB$向右平移$a$个单位长度,则平移后的点$A(a,4)$,$C(\frac{3}{2} + a,2)$。
∵反比例函数$y = \frac{k}{x}(k \neq 0,x > 0)$的图像恰好经过平移后的点$A(a,4)$,$C(\frac{3}{2} + a,2)$,
∴$k = 4a = 2(\frac{3}{2} + a)$,解得$a = \frac{3}{2}$,
∴平移的长度是$\frac{3}{2}$。故答案为$\frac{3}{2}$。
∵$Rt\triangle OAB$的一条边$OA$在$y$轴上,$OA = 4$,$AB = 3$,
∴$A(0,4)$,$B(3,4)$,
∴$OB$的中点$C(\frac{3}{2},2)$。设$\triangle OAB$向右平移$a$个单位长度,则平移后的点$A(a,4)$,$C(\frac{3}{2} + a,2)$。
∵反比例函数$y = \frac{k}{x}(k \neq 0,x > 0)$的图像恰好经过平移后的点$A(a,4)$,$C(\frac{3}{2} + a,2)$,
∴$k = 4a = 2(\frac{3}{2} + a)$,解得$a = \frac{3}{2}$,
∴平移的长度是$\frac{3}{2}$。故答案为$\frac{3}{2}$。
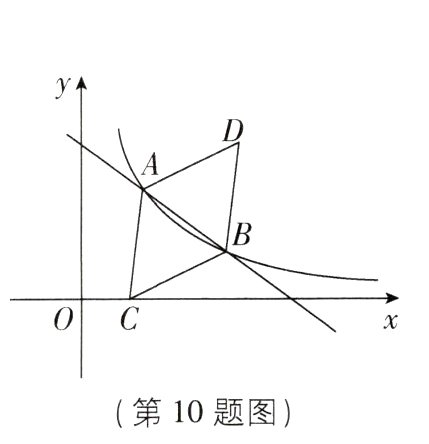
10[2023江苏无锡期中]如图,已知一次函数$y = mx + n$的图像与反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图像交于A$(3,a)$,B$(14 - 2a,2)$两点,点C是x轴上一点,点D是坐标平面内一点,若四边形ACBD是以AB为对角线的菱形,则点C的坐标为________.

答案:
$(\frac{5}{2},0)$【解析】
∵点$A(3,a)$,点$B(14 - 2a,2)$在反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图像上,
∴$3×a = (14 - 2a)×2$,解得$a = 4$,
∴$A(3,4)$,$B(6,2)$。过点$A$作$AE \perp x$轴于点$E$,过点$B$作$BF \perp x$轴于点$F$,如图,则$AE = 4$,$BF = 2$。
∵点$C$在$x$轴上,
∴设点$C$的坐标为$(x,0)$,
∴$OC = x$,
∴$CE = 3 - x$,$CF = 6 - x$。由勾股定理得,$AE^2 + CE^2 = AC^2$,$BF^2 + CF^2 = BC^2$。又
∵四边形$ACBD$是菱形,
∴$AC = CB$,
∴$AE^2 + CE^2 = BF^2 + CF^2$,即$4^2 + (3 - x)^2 = 2^2 + (6 - x)^2$,解得$x = \frac{5}{2}$,
∴点$C$的坐标为$(\frac{5}{2},0)$。

$(\frac{5}{2},0)$【解析】
∵点$A(3,a)$,点$B(14 - 2a,2)$在反比例函数$y = \frac{k}{x}(k > 0,x > 0)$的图像上,
∴$3×a = (14 - 2a)×2$,解得$a = 4$,
∴$A(3,4)$,$B(6,2)$。过点$A$作$AE \perp x$轴于点$E$,过点$B$作$BF \perp x$轴于点$F$,如图,则$AE = 4$,$BF = 2$。
∵点$C$在$x$轴上,
∴设点$C$的坐标为$(x,0)$,
∴$OC = x$,
∴$CE = 3 - x$,$CF = 6 - x$。由勾股定理得,$AE^2 + CE^2 = AC^2$,$BF^2 + CF^2 = BC^2$。又
∵四边形$ACBD$是菱形,
∴$AC = CB$,
∴$AE^2 + CE^2 = BF^2 + CF^2$,即$4^2 + (3 - x)^2 = 2^2 + (6 - x)^2$,解得$x = \frac{5}{2}$,
∴点$C$的坐标为$(\frac{5}{2},0)$。

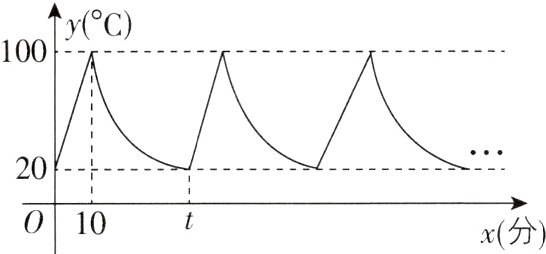
11[2024浙江杭州拱墅区二模]小丽家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y(℃)与开机时间x(分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y(℃)与开机时间x(分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热,…,重复上述程序(如图所示),根据图中提供的信息,解答问题:
(1)当$0 \leq x \leq 10$时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小丽在通电开机后立即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的水温约为多少?
(1)当$0 \leq x \leq 10$时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小丽在通电开机后立即外出散步,请你预测小丽散步70分钟回到家时,饮水机内的水温约为多少?

答案:
【解】
(1)当$0 \leq x \leq 10$时,设水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = kx + b$。依据题意,得$\begin{cases}b = 20 \\ 10k + b = 100\end{cases}$,解得$\begin{cases}k = 8 \\ b = 20\end{cases}$,
∴此函数关系式为$y = 8x + 20$。
(2)当$10 < x \leq t$时,设水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = \frac{m}{x}$。依据题意,得$100 = \frac{m}{10}$,
∴$m = 1000$,故$y = \frac{1000}{x}$。
当$y = 20$时,$20 = \frac{1000}{t}$,解得$t = 50$。
(3)
∵$70 - 50 = 20 > 10$,
∴当$x = 20$时,$y = \frac{1000}{20} = 50$。
答:小丽散步 70 分钟回到家时,饮水机内的水温约为$50^{\circ}C$。
(1)当$0 \leq x \leq 10$时,设水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = kx + b$。依据题意,得$\begin{cases}b = 20 \\ 10k + b = 100\end{cases}$,解得$\begin{cases}k = 8 \\ b = 20\end{cases}$,
∴此函数关系式为$y = 8x + 20$。
(2)当$10 < x \leq t$时,设水温$y(^{\circ}C)$与开机时间$x$(分)的函数关系式为$y = \frac{m}{x}$。依据题意,得$100 = \frac{m}{10}$,
∴$m = 1000$,故$y = \frac{1000}{x}$。
当$y = 20$时,$20 = \frac{1000}{t}$,解得$t = 50$。
(3)
∵$70 - 50 = 20 > 10$,
∴当$x = 20$时,$y = \frac{1000}{20} = 50$。
答:小丽散步 70 分钟回到家时,饮水机内的水温约为$50^{\circ}C$。
12[2023四川巴中中考]如图,正比例函数$y = kx$($k \neq 0$)与反比例函数$y = \frac{m}{x}$($m \neq 0$)的图像交于A,B两点,A的横坐标为-4,B的纵坐标为-6.
(1)求反比例函数的表达式.
(2)观察图像,直接写出不等式$kx < \frac{m}{x}$的解集.
(3)将直线AB向上平移n个单位,交双曲线于C,D两点,交坐标轴于点E,F,连结OD,BD,若$\triangle OBD$的面积为20,求直线CD的表达式.
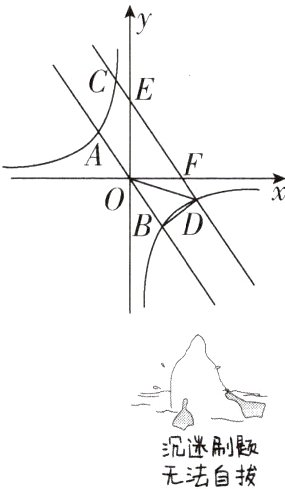
(1)求反比例函数的表达式.
(2)观察图像,直接写出不等式$kx < \frac{m}{x}$的解集.
(3)将直线AB向上平移n个单位,交双曲线于C,D两点,交坐标轴于点E,F,连结OD,BD,若$\triangle OBD$的面积为20,求直线CD的表达式.

答案:
【解】
(1)
∵直线$y = kx(k \neq 0)$与双曲线$y = \frac{m}{x}(m \neq 0)$交于$A$,$B$两点,
∴$A$,$B$关于原点对称。
∵$x_A = -4$,$y_B = -6$,
∴$A(-4,6)$,$B(4,-6)$。
∵$A(-4,6)$在双曲线$y = \frac{m}{x}(m \neq 0)$上,
∴$6 = \frac{m}{-4}$,
∴$m = -24$,
∴反比例函数的表达式为$y = -\frac{24}{x}$。
(2)观察函数图像可知,当$-4 < x < 0$或$x > 4$时,直线$y = kx(k \neq 0)$在双曲线$y = \frac{m}{x}(m \neq 0)$的下方,
∴不等式$kx < \frac{m}{x}$的解集为$-4 < x < 0$或$x > 4$。
(3)如图,连接$BE$,作$BG \perp y$轴于点$G$。设直线$CD$的表达式为$y = k'x + n$。

∵$A(-4,6)$在直线$y = kx$上,
∴$6 = -4k$,解得$k = -\frac{3}{2}$,
∴直线$AB$的表达式为$y = -\frac{3}{2}x$。
∵$CD // AB$,
∴$S_{\triangle OBD} = S_{\triangle OBE} = 20$。
∵$B(4,-6)$,
∴$BG = 4$,
∴$S_{\triangle OBE} = \frac{1}{2}OE \cdot BG = 20$,
∴$OE = 10$,
∴$E(0,10)$,
∴$n = 10$。
∵由平移可知$CD // AB$,
∴$k' = k = -\frac{3}{2}$,
∴直线$CD$的表达式为$y = -\frac{3}{2}x + 10$。
【解】
(1)
∵直线$y = kx(k \neq 0)$与双曲线$y = \frac{m}{x}(m \neq 0)$交于$A$,$B$两点,
∴$A$,$B$关于原点对称。
∵$x_A = -4$,$y_B = -6$,
∴$A(-4,6)$,$B(4,-6)$。
∵$A(-4,6)$在双曲线$y = \frac{m}{x}(m \neq 0)$上,
∴$6 = \frac{m}{-4}$,
∴$m = -24$,
∴反比例函数的表达式为$y = -\frac{24}{x}$。
(2)观察函数图像可知,当$-4 < x < 0$或$x > 4$时,直线$y = kx(k \neq 0)$在双曲线$y = \frac{m}{x}(m \neq 0)$的下方,
∴不等式$kx < \frac{m}{x}$的解集为$-4 < x < 0$或$x > 4$。
(3)如图,连接$BE$,作$BG \perp y$轴于点$G$。设直线$CD$的表达式为$y = k'x + n$。

∵$A(-4,6)$在直线$y = kx$上,
∴$6 = -4k$,解得$k = -\frac{3}{2}$,
∴直线$AB$的表达式为$y = -\frac{3}{2}x$。
∵$CD // AB$,
∴$S_{\triangle OBD} = S_{\triangle OBE} = 20$。
∵$B(4,-6)$,
∴$BG = 4$,
∴$S_{\triangle OBE} = \frac{1}{2}OE \cdot BG = 20$,
∴$OE = 10$,
∴$E(0,10)$,
∴$n = 10$。
∵由平移可知$CD // AB$,
∴$k' = k = -\frac{3}{2}$,
∴直线$CD$的表达式为$y = -\frac{3}{2}x + 10$。
查看更多完整答案,请扫码查看


