第33页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2024安徽宣城模拟]如图,□ABCD的对角线交于点O,添加下列条件不能判断四边形ABCD是菱形的是( )
A. ∠BAC = ∠DAC B. ∠ABD = ∠CBD
C. △AOB≌△COB D. △ABD≌△CDB
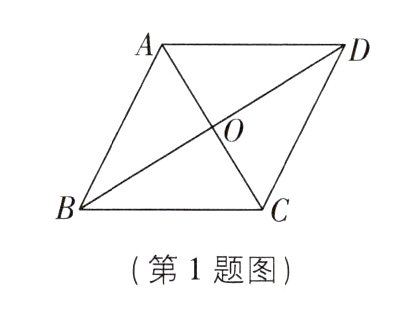
A. ∠BAC = ∠DAC B. ∠ABD = ∠CBD
C. △AOB≌△COB D. △ABD≌△CDB

答案:
D【解析】A选项,
∵ 四边形ABCD是平行四边形,
∴ AB $//$ CD,
∴ $\angle ACD=\angle BAC$。
∵ $\angle BAC = \angle DAC$,
∴ $\angle ACD=\angle DAC$,
∴ AD = CD,
∴ 四边形ABCD是菱形,故A不符合题意;B选项,当添加$\angle ABD=\angle CBD$时,同理可证明四边形ABCD是菱形,故B不符合题意;C选项,
∵ $\triangle AOB\cong\triangle COB$,
∴ AB = BC,
∴ 四边形ABCD是菱形,故C不符合题意;D选项,添加$\triangle ABD\cong\triangle CDB$不能证明四边形ABCD是菱形,故D符合题意。故选D。
∵ 四边形ABCD是平行四边形,
∴ AB $//$ CD,
∴ $\angle ACD=\angle BAC$。
∵ $\angle BAC = \angle DAC$,
∴ $\angle ACD=\angle DAC$,
∴ AD = CD,
∴ 四边形ABCD是菱形,故A不符合题意;B选项,当添加$\angle ABD=\angle CBD$时,同理可证明四边形ABCD是菱形,故B不符合题意;C选项,
∵ $\triangle AOB\cong\triangle COB$,
∴ AB = BC,
∴ 四边形ABCD是菱形,故C不符合题意;D选项,添加$\triangle ABD\cong\triangle CDB$不能证明四边形ABCD是菱形,故D符合题意。故选D。
2[2024江苏南京质检]如图,剪两张对边平行的纸条,纸条宽度相等,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形,则这个四边形是_______.


答案:
菱形【解析】如图,过点D分别作DM $\perp$ BC于点M,DN $\perp$ AB于点N。
∵ AB $//$ CD,AD $//$ BC,
∴ 四边形ABCD是平行四边形,
∴ $\angle DAN=\angle DCM$。
∵ 纸条宽度相等,
∴ DN = DM。在$\triangle ADN$和$\triangle CDM$中,$\begin{cases}\angle DAN=\angle DCM\\\angle AND=\angle CMD\\DN = DM\end{cases}$,
∴ $\triangle ADN\cong\triangle CDM(AAS)$,
∴ AD = DC,
∴ 平行四边形ABCD是菱形。

菱形【解析】如图,过点D分别作DM $\perp$ BC于点M,DN $\perp$ AB于点N。
∵ AB $//$ CD,AD $//$ BC,
∴ 四边形ABCD是平行四边形,
∴ $\angle DAN=\angle DCM$。
∵ 纸条宽度相等,
∴ DN = DM。在$\triangle ADN$和$\triangle CDM$中,$\begin{cases}\angle DAN=\angle DCM\\\angle AND=\angle CMD\\DN = DM\end{cases}$,
∴ $\triangle ADN\cong\triangle CDM(AAS)$,
∴ AD = DC,
∴ 平行四边形ABCD是菱形。

3如图,若AB = 2 cm,四边形OACB的面积为4 cm²,则OC的长为________ cm.


答案:
4【解析】根据作图可得OA = OB = BC = AC,
(1)根据角平分线的性质和等腰三角形的性质得出∠FAD=∠B,进而得到AD//BC,再利用∠DCE=∠ACD,即可证得△ABC和△ADC是等边三角形,进而得到AD=CB=AB=CD,可判定四边形ABCD是菱形。易错警示:要判定一个图形是菱形,先看它的前提条件,若是四边形,则证明其四条边都相等,或者先证明它是平行四边形,再找一组邻边相等或对角线互相垂直;若是平行四边形,则需要找一组邻边相等或对角线互相垂直。做平行题时不能忽略菱形的判定的前提条件。
∴ 四边形OACB是菱形。
∵ AB = 2 cm,四边形OACB的面积为4 $cm^{2}$,
∴ $\frac{1}{2}AB\cdot OC=\frac{1}{2}\times2\times OC = 4$,解得OC = 4 cm。故答案为4。
(1)根据角平分线的性质和等腰三角形的性质得出∠FAD=∠B,进而得到AD//BC,再利用∠DCE=∠ACD,即可证得△ABC和△ADC是等边三角形,进而得到AD=CB=AB=CD,可判定四边形ABCD是菱形。易错警示:要判定一个图形是菱形,先看它的前提条件,若是四边形,则证明其四条边都相等,或者先证明它是平行四边形,再找一组邻边相等或对角线互相垂直;若是平行四边形,则需要找一组邻边相等或对角线互相垂直。做平行题时不能忽略菱形的判定的前提条件。
∴ 四边形OACB是菱形。
∵ AB = 2 cm,四边形OACB的面积为4 $cm^{2}$,
∴ $\frac{1}{2}AB\cdot OC=\frac{1}{2}\times2\times OC = 4$,解得OC = 4 cm。故答案为4。
4如图,在△ABC中,AB = AC,AD,CD分别平分△ABC的两个外角.
(1)求证:∠ACD = ∠ADC;
(2)若∠B = 60°,求证:四边形ABCD是菱形.
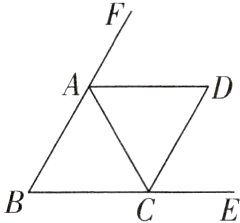
(1)求证:∠ACD = ∠ADC;
(2)若∠B = 60°,求证:四边形ABCD是菱形.

答案:
【证明】
(1)
∵ AB = AC,
∴ $\angle B=\angle ACB$,
∴ $\angle FAC=\angle B+\angle ACB = 2\angle B$。
∵ AD平分$\angle FAC$,
∴ $\angle FAC = 2\angle FAD$,
∴ $\angle FAD=\angle B$,
∴ AD $//$ BC,
∴ $\angle ADC=\angle DCE$。
∵ CD平分$\angle ACE$,
∴ $\angle ACD=\angle DCE$,
∴ $\angle ACD=\angle ADC$。
(2)
∵ AB = AC,$\angle B = 60^{\circ}$,AD $//$ BC,
∴ $\angle ACB=\angle CAD = 60^{\circ}$。
∵ $\angle ACD=\angle ADC$,
∴ $\triangle ABC$和$\triangle ACD$都是等边三角形,
∴ AB = BC = AC = CD = AD,
∴ 四边形ABCD是菱形。
(1)
∵ AB = AC,
∴ $\angle B=\angle ACB$,
∴ $\angle FAC=\angle B+\angle ACB = 2\angle B$。
∵ AD平分$\angle FAC$,
∴ $\angle FAC = 2\angle FAD$,
∴ $\angle FAD=\angle B$,
∴ AD $//$ BC,
∴ $\angle ADC=\angle DCE$。
∵ CD平分$\angle ACE$,
∴ $\angle ACD=\angle DCE$,
∴ $\angle ACD=\angle ADC$。
(2)
∵ AB = AC,$\angle B = 60^{\circ}$,AD $//$ BC,
∴ $\angle ACB=\angle CAD = 60^{\circ}$。
∵ $\angle ACD=\angle ADC$,
∴ $\triangle ABC$和$\triangle ACD$都是等边三角形,
∴ AB = BC = AC = CD = AD,
∴ 四边形ABCD是菱形。
5[2023陕西咸阳秦都区二模]如图,□ABCD的对角线AC与BD相交于点O,添加下列条件不能证明□ABCD是菱形的是( )
A. ∠ABD = ∠ADB B. AC⊥BD
C. AB = BC D. AC = BD

A. ∠ABD = ∠ADB B. AC⊥BD
C. AB = BC D. AC = BD

答案:
D【解析】

A:
∵ $\angle ABD=\angle ADB$,
∴ AB = AD,
∴ $\square ABCD$是菱形,故A不符合题意。
B:
∵ 四边形ABCD是平行四边形,AC $\perp$ BD,
∴ $\square ABCD$是菱形,故B不符合题意。
C:
∵ 四边形ABCD是平行四边形,AB = BC,
∴ $\square ABCD$是菱形,故C不符合题意。
D:
∵ 四边形ABCD是平行四边形,AC = BD,
∴ $\square ABCD$是矩形,故D符合题意。
D【解析】

A:
∵ $\angle ABD=\angle ADB$,
∴ AB = AD,
∴ $\square ABCD$是菱形,故A不符合题意。
B:
∵ 四边形ABCD是平行四边形,AC $\perp$ BD,
∴ $\square ABCD$是菱形,故B不符合题意。
C:
∵ 四边形ABCD是平行四边形,AB = BC,
∴ $\square ABCD$是菱形,故C不符合题意。
D:
∵ 四边形ABCD是平行四边形,AC = BD,
∴ $\square ABCD$是矩形,故D符合题意。
6[2024湖北武汉江汉区期中]如图,已知□ABCD,E,F是对角线BD上的两点,BE = DF,连接AE,CE,AF,CF.
(1)求证:AE = CF;
(2)连接AC交BD于O,直接写出当AC和BD满足什么关系时,四边形AECF是菱形.
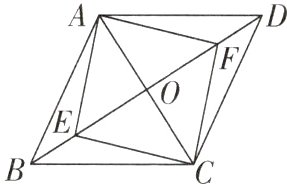
(1)求证:AE = CF;
(2)连接AC交BD于O,直接写出当AC和BD满足什么关系时,四边形AECF是菱形.

答案:
(1) 【证明】
∵ 四边形ABCD是平行四边形,
∴ AB = CD,AB $//$ CD,
∴ $\angle ABE=\angle CDF$。又
∵ BE = DF,
∴ $\triangle ABE\cong\triangle CDF(SAS)$,
∴ AE = CF。
(2) 【解】AC $\perp$ BD时,四边形AECF是菱形。理由如下:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,OB = OD。
∵ BE = DF,
∴ OB - BE = OD - DF,即OE = OF,
∴ 四边形AECF是平行四边形。又
∵ AC $\perp$ BD,
∴ 平行四边形AECF是菱形。
(1) 【证明】
∵ 四边形ABCD是平行四边形,
∴ AB = CD,AB $//$ CD,
∴ $\angle ABE=\angle CDF$。又
∵ BE = DF,
∴ $\triangle ABE\cong\triangle CDF(SAS)$,
∴ AE = CF。
(2) 【解】AC $\perp$ BD时,四边形AECF是菱形。理由如下:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,OB = OD。
∵ BE = DF,
∴ OB - BE = OD - DF,即OE = OF,
∴ 四边形AECF是平行四边形。又
∵ AC $\perp$ BD,
∴ 平行四边形AECF是菱形。
7小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD交于点O,AC⊥BD,OB = OD. 求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠:
证明:∵AC⊥BD,OB = OD,
∴AC垂直平分BD,
∴AB = AD,CB = CD,
∴四边形ABCD是菱形
小洁:
这个题目还缺少条件,需要补充一个条件才能证明
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件并证明.

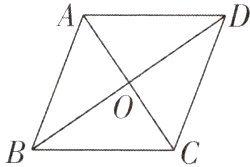
小惠:
证明:∵AC⊥BD,OB = OD,
∴AC垂直平分BD,
∴AB = AD,CB = CD,
∴四边形ABCD是菱形
小洁:
这个题目还缺少条件,需要补充一个条件才能证明
若赞同小惠的证法,请在第一个方框内打“√”;若赞成小洁的说法,请你补充一个条件并证明.


答案:
【解】赞成小洁的说法,补充条件:OA = OC。证明:
∵ OA = OC,OB = OD,
∴ 四边形ABCD是平行四边形。又
∵ AC $\perp$ BD,
∴ 平行四边形ABCD是菱形。(补充的条件不唯一)
∵ OA = OC,OB = OD,
∴ 四边形ABCD是平行四边形。又
∵ AC $\perp$ BD,
∴ 平行四边形ABCD是菱形。(补充的条件不唯一)
查看更多完整答案,请扫码查看


