第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[2024北京石景山区二模]中国的航天事业蓬勃发展,取得了显著的进展和突破.下列航天图标中,其文字上方的图案是中心对称图形的是( )




答案:
C [解析]A选项,中国探月图标旋转180°后,不能与原图形重合,不是中心对称图形,故此选项不符合题意;B选项,中国航天图标旋转180°后,不能与原图形重合,不是中心对称图形,故此选项不符合题意;C选项,中国火箭图标旋转180°后,能与原图形重合,是中心对称图形,故此选项符合题意;D选项,中国行星探测图标旋转180°后,不能与原图形重合,不是中心对称图形,故此选项不符合题意.故选C.
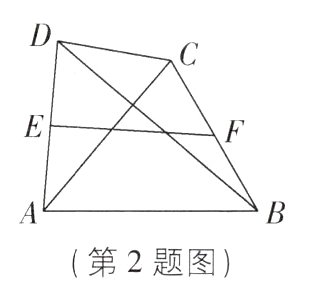
2[2024江苏南京鼓楼区调研]如图,已知四边形ABCD中,AC⊥BD,AC = 6,BD = 8,点E,F分别是边AD,BC的中点,连接EF,则EF的长是( )
A. $\sqrt{24}$
B.5
C.$\sqrt{32}$
D.10

A. $\sqrt{24}$
B.5
C.$\sqrt{32}$
D.10
答案:
B [解析]如图,取AB的中点G,连接EG,FG;

∵E,F分别是边AD,CB的中点,
∴EG//BD且EG=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,FG//AC且FG=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3.
∵AC⊥BD,
∴EG⊥FG,
∴EF=$\sqrt{EG^{2}+FG^{2}}$=$\sqrt{4^{2}+3^{2}}$=5.
B [解析]如图,取AB的中点G,连接EG,FG;

∵E,F分别是边AD,CB的中点,
∴EG//BD且EG=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,FG//AC且FG=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3.
∵AC⊥BD,
∴EG⊥FG,
∴EF=$\sqrt{EG^{2}+FG^{2}}$=$\sqrt{4^{2}+3^{2}}$=5.
3[2024江苏南通二模]如图,在菱形ABCD中,∠B = α,点P是AB上一点(不与端点重合),点A关于直线DP的对称点为E,连接AE,CE,则∠AEC的度数为( )
A.60°+$\frac{1}{3}$α
B.165°−$\frac{1}{3}$α
C.45°+$\frac{1}{2}$α
D.180°−$\frac{1}{2}$α
A.60°+$\frac{1}{3}$α
B.165°−$\frac{1}{3}$α
C.45°+$\frac{1}{2}$α
D.180°−$\frac{1}{2}$α
答案:
D [解析]连接DE,如图. 由点A关于直线DP的对称点为E,得DA=DE,
∴∠DAE=∠DEA. 由菱形ABCD可得AD=DC,∠B=∠ADC=α,
∴DE=DC,
∴∠DEC=∠DCE. 在四边形AECD中,∠ADC+∠DAE+∠DEA+∠DEC+∠DCE=360°,
∴∠ADC+2∠AEC=360°,
∴α+2∠AEC=360°,
∴∠AEC=180°-$\frac{1}{2}$α,故选D.

D [解析]连接DE,如图. 由点A关于直线DP的对称点为E,得DA=DE,
∴∠DAE=∠DEA. 由菱形ABCD可得AD=DC,∠B=∠ADC=α,
∴DE=DC,
∴∠DEC=∠DCE. 在四边形AECD中,∠ADC+∠DAE+∠DEA+∠DEC+∠DCE=360°,
∴∠ADC+2∠AEC=360°,
∴α+2∠AEC=360°,
∴∠AEC=180°-$\frac{1}{2}$α,故选D.

4[2024北京海淀区期中]如图,点A,B,C为平面内不在同一直线上的三点.点D为平面内一个动点.线段AB,BC,CD,DA的中点分别为M,N,P,Q.在点D的运动过程中,有下列结论:①存在无数个中点四边形MNPQ是平行四边形;②存在无数个中点四边形MNPQ是菱形;③存在无数个中点四边形MNPQ是矩形;④存在无数个中点四边形MNPQ是正方形.其中,正确的结论有( )
A.①②③
B.②③④
C.①②④
D.①③④
A.①②③
B.②③④
C.①②④
D.①③④
答案:
A [解析]连接AC,BD.
∵AB,BC,CD,DA的中点分别为M,N,P,Q,
∴PQ//AC,PQ=$\frac{1}{2}$AC,MN//AC,NM=$\frac{1}{2}$AC,PN//BD,PN=$\frac{1}{2}$BD,QM//BD,QM=$\frac{1}{2}$BD,
∴PQ//MN,PQ=MN,QM//PN,QM=PN. ①当AC与BD不平行时,如图
(1),
∵PQ//MN,PQ=MN,
∴中点四边形MNPQ是平行四边形,故存在无数个中点四边形MNPQ是平行四边形.


②当AC=BD且AC与BD不平行时,如图
(2),
∵PQ=MN=$\frac{1}{2}$AC,QM=PN=$\frac{1}{2}$BD,AC=BD,
∴PQ=MN=QM=PN,
∴中点四边形MNPQ是菱形,故存在无数个中点四边形MNPQ是菱形.
③当AC⊥BD(B,D不重合)时,如图
(3),
∵PQ//MN//AC,QM//PN//BD,AC⊥BD,
∴PQ⊥PN,
∴中点四边形MNPQ是矩形,故存在无数个中点四边形MNPQ是矩形.



本题考查中点四边形,关键是利用原四边形对角线的关系推出中点四边形四边的关系从而判定形状
④当AC⊥BD,AC=BD时,如图
(4),图
(5),
∵PQ//MN//AC,QM//PN//BD,AC⊥BD,
∴PQ⊥PN.
∵PQ=MN=$\frac{1}{2}$AC,QM=PN=$\frac{1}{2}$BD,AC=BD,
∴PQ=MN=QM=PN,
∴中点四边形MNPQ是正方形,故存在两个中点四边形MNPQ是正方形.综上,正确的结论有①②③,故选A.
A [解析]连接AC,BD.
∵AB,BC,CD,DA的中点分别为M,N,P,Q,
∴PQ//AC,PQ=$\frac{1}{2}$AC,MN//AC,NM=$\frac{1}{2}$AC,PN//BD,PN=$\frac{1}{2}$BD,QM//BD,QM=$\frac{1}{2}$BD,
∴PQ//MN,PQ=MN,QM//PN,QM=PN. ①当AC与BD不平行时,如图
(1),
∵PQ//MN,PQ=MN,
∴中点四边形MNPQ是平行四边形,故存在无数个中点四边形MNPQ是平行四边形.


②当AC=BD且AC与BD不平行时,如图
(2),
∵PQ=MN=$\frac{1}{2}$AC,QM=PN=$\frac{1}{2}$BD,AC=BD,
∴PQ=MN=QM=PN,
∴中点四边形MNPQ是菱形,故存在无数个中点四边形MNPQ是菱形.
③当AC⊥BD(B,D不重合)时,如图
(3),
∵PQ//MN//AC,QM//PN//BD,AC⊥BD,
∴PQ⊥PN,
∴中点四边形MNPQ是矩形,故存在无数个中点四边形MNPQ是矩形.



本题考查中点四边形,关键是利用原四边形对角线的关系推出中点四边形四边的关系从而判定形状
④当AC⊥BD,AC=BD时,如图
(4),图
(5),
∵PQ//MN//AC,QM//PN//BD,AC⊥BD,
∴PQ⊥PN.
∵PQ=MN=$\frac{1}{2}$AC,QM=PN=$\frac{1}{2}$BD,AC=BD,
∴PQ=MN=QM=PN,
∴中点四边形MNPQ是正方形,故存在两个中点四边形MNPQ是正方形.综上,正确的结论有①②③,故选A.
5新考法正方形ABCD的对角线相交于点O(如图(1)),如果∠BOC绕点O按顺时针方向旋转,其两边分别与边AB,BC相交于点E,F(如图(2)),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )

A.线段
B.圆弧
C.折线
D.波浪线

A.线段
B.圆弧
C.折线
D.波浪线
答案:
A [解析]建立如图所示的平面直角坐标系,设正方形ABCD的边长为1.
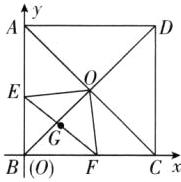
∵四边形ABCD是正方形,
∴∠OAE=∠OBF=45°,OA=OB.
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴AE=BF. 设AE=BF=a,则F(a,0),E(0,1−a).
∵EG=FG,
∴G($\frac{1}{2}$a,$\frac{1}{2}$−$\frac{1}{2}$a),
∴点G在直线y=−x+$\frac{1}{2}$(位于正方形ABCD内)上运动,
∴点G经过的路线是线段.故选A.
A [解析]建立如图所示的平面直角坐标系,设正方形ABCD的边长为1.

∵四边形ABCD是正方形,
∴∠OAE=∠OBF=45°,OA=OB.
∵∠AOB=∠EOF=90°,
∴∠AOE=∠BOF,
∴△AOE≌△BOF(ASA),
∴AE=BF. 设AE=BF=a,则F(a,0),E(0,1−a).
∵EG=FG,
∴G($\frac{1}{2}$a,$\frac{1}{2}$−$\frac{1}{2}$a),
∴点G在直线y=−x+$\frac{1}{2}$(位于正方形ABCD内)上运动,
∴点G经过的路线是线段.故选A.
6[2023江苏苏州质检]如图,矩形ABCD中,AB = 4,AD = 2,E为AB的中点,连接ED,EC,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )

A.2
B.4
C.$\sqrt{2}$
D.$\sqrt{8}$

A.2
B.4
C.$\sqrt{2}$
D.$\sqrt{8}$
答案:
D [解析]如图,当点F与点C重合时,点P在P₁处,且CP₁=DP₁;当点F与点E重合时,点P在P₂处,且EP₂=DP₂,
∴P₁P₂//CE且P₁P₂=$\frac{1}{2}$CE.当点F在EC上除点C,E的位置时,DP=FP.由中位线定理可知P₁P//CE且P₁P=$\frac{1}{2}$CF,
∴点P的运动轨迹是线段P₁P₂,
∴当BP⊥P₁P₂时,PB取得最小值.
∵矩形ABCD中,AB=4,AD=2,E为AB的中点,
∴AD=AE=BE=BC=CP₁=2,∠A=∠ABC=∠BCD=90°,
∴△CBE,△ADE,△BCP₁为等腰直角三角形,
∴∠ADE=∠CDE=∠CP₁B=45°,∠DEC=90°,
∴∠DP₂P₁=90°,
∴∠DP₁P₂=45°,
∴∠P₂P₁B=90°,即BP₁⊥P₁P₂,
∴BP的最小值为BP₁的长.在等腰直角三角形BCP₁中,CP₁=BC=2,由勾股定理得BP₁=$\sqrt{8}$,
∴PB的最小值是$\sqrt{8}$.故选D.

D [解析]如图,当点F与点C重合时,点P在P₁处,且CP₁=DP₁;当点F与点E重合时,点P在P₂处,且EP₂=DP₂,
∴P₁P₂//CE且P₁P₂=$\frac{1}{2}$CE.当点F在EC上除点C,E的位置时,DP=FP.由中位线定理可知P₁P//CE且P₁P=$\frac{1}{2}$CF,
∴点P的运动轨迹是线段P₁P₂,
∴当BP⊥P₁P₂时,PB取得最小值.
∵矩形ABCD中,AB=4,AD=2,E为AB的中点,
∴AD=AE=BE=BC=CP₁=2,∠A=∠ABC=∠BCD=90°,
∴△CBE,△ADE,△BCP₁为等腰直角三角形,
∴∠ADE=∠CDE=∠CP₁B=45°,∠DEC=90°,
∴∠DP₂P₁=90°,
∴∠DP₁P₂=45°,
∴∠P₂P₁B=90°,即BP₁⊥P₁P₂,
∴BP的最小值为BP₁的长.在等腰直角三角形BCP₁中,CP₁=BC=2,由勾股定理得BP₁=$\sqrt{8}$,
∴PB的最小值是$\sqrt{8}$.故选D.

7[2023江苏苏州工业园区二模]如图,□ABCD的顶点A(0,4),B(-3,0),以点B为圆心,AB长为半径画弧,交BC于点E,分别以点A,E为圆心,大于$\frac{1}{2}AE$的长为半径画弧,两弧在∠ABE的内部相交于点F,画射线BF交AD于点G,则点G的坐标是________.


答案:
(5,4) [解析]
∵▱ABCD的顶点A(0,4),B(−3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{OB^{2}+OA^{2}}$=$\sqrt{3^{2}+4^{2}}$=5.根据作图可知,BG是∠ABC的平分线,
∴∠ABG=∠GBC.在▱ABCD中,AD//BC,
∴∠AGB=∠GBC,点G 的纵坐标与点A的纵坐标相等,
∴∠ABG=∠AGB,
∴AG=AB=5,
∴点G的坐标是(5,4),故答案为(5,4).
∵▱ABCD的顶点A(0,4),B(−3,0),
∴OA=4,OB=3,
∴AB=$\sqrt{OB^{2}+OA^{2}}$=$\sqrt{3^{2}+4^{2}}$=5.根据作图可知,BG是∠ABC的平分线,
∴∠ABG=∠GBC.在▱ABCD中,AD//BC,
∴∠AGB=∠GBC,点G 的纵坐标与点A的纵坐标相等,
∴∠ABG=∠AGB,
∴AG=AB=5,
∴点G的坐标是(5,4),故答案为(5,4).
查看更多完整答案,请扫码查看


