《2025年初中必刷题八年级数学下册苏科版》

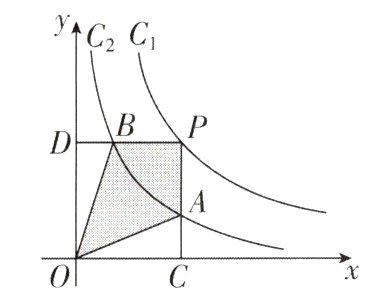
6[中]两个反比例函数$C_1:y=\frac{2}{x}$和$C_2:y=\frac{1}{x}$在第一象限内的图像如图所示，设点P在$C_1$上，PC⊥x轴于点C，交$C_2$于点A，PD⊥y轴于点D，交$C_2$于点B，则四边形PAOB的面积为 ( )

A. 1
B. 2
C. 3
D. 4

答案： 6. A 【解析】$\because PC \perp x$轴，$PD \perp y$轴，$\therefore S_{\triangle AOC} = S_{\triangle BOD} = \frac{1}{2} \times \vert 1 \vert = \frac{1}{2}$，$S_{矩形PCOD} = \vert 2 \vert = 2$，$\therefore$ 四边形$PAOB$的面积为$2 - 2 \times \frac{1}{2} = 1$。

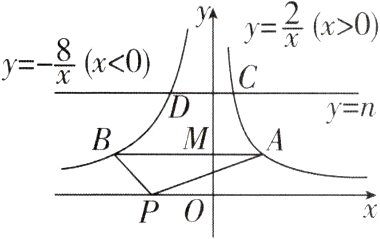
7[2024安徽安庆调研，中]已知反比例函数$y=\frac{2}{x}(x＞0)$和反比例函数$y=-\frac{8}{x}(x＜0)$的图像如图所示.
(1)点A在反比例函数$y=\frac{2}{x}(x＞0)$的图像上，过点A作y轴的垂线交反比例函数$y=-\frac{8}{x}(x＜0)$的图像于点B，交y轴于点M，点P在x轴上，连接PA，PB，求△PAB的面积；
(2)直线y = n(n＞0)交反比例函数$y=\frac{2}{x}(x＞0)$的图像于点C，交反比例函数$y=-\frac{8}{x}(x＜0)$的图像于点D，若CD = 4，求n的值.

答案：
【解】
(1)如图，连接$OA$，$OB$。$\because AB \perp y$轴，$\therefore S_{\triangle OAM} = 1$，$S_{\triangle OBM} = 4$，$\therefore S_{\triangle OAB} = S_{\triangle OAM} + S_{\triangle OBM} = 1 + 4 = 5$。$\because AB // x$轴，$\therefore S_{\triangle PAB} = S_{\triangle OAB} = 5$。
(2)当$y_C = y_D = n$时，$y_C = \frac{2}{x_C} = n$，$y_D = -\frac{8}{x_D} = n$，
$\therefore x_C = \frac{2}{n}$，$x_D = -\frac{8}{n}$，$\therefore CD = \frac{2}{n} - (-\frac{8}{n}) = \frac{10}{n}$。
$\because CD = 4$，$\therefore \frac{10}{n} = 4$，解得$n = \frac{5}{2}$，经检验，$n = \frac{5}{2}$是分式方程的解，$\therefore n = \frac{5}{2}$。

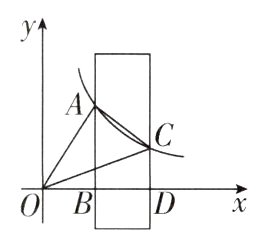
8[新考法][2024广东佛山顺德区质检，中]如图，平行于y轴的直尺(部分)与反比例函数$y=\frac{m}{x}(x＞0)$的图像交于A，C两点，与x轴交于B，D两点，点A，B对应直尺上的刻度分别为5，2，直尺的宽度BD = 2，$S_{\triangle AOC}=5$，则点C的坐标是________.

答案： $(6, 2)$ 【解析】$\because$ 直尺平行于$y$轴，$A$，$B$对应直尺的刻度分别为$5$，$2$，$\therefore AB = 3$，则$A$的坐标为$(\frac{m}{3}, 3)$，则$D$的坐标为$(\frac{m}{3} + 2, 0)$，
关键点拨
过$E$作$EC \perp x$轴于$C$，过$F$作$FD \perp x$轴于$D$，将$\triangle EOF$的面积转化为梯形$ECDF$的面积求解即可。
思路分析
设点$A$横坐标为$a$，则可得到点$A$，$B$的坐标，进而得到$a^2 = 2a(2a - 1)$，解之即可。
$\therefore C(\frac{m}{3} + 2, \frac{3m}{m + 6})$。$\because S_{\triangle AOC} = S_{\triangle AOB} + S_{梯形ABDC} - S_{\triangle OCD} = 5$，$S_{\triangle AOB} = S_{\triangle OCD}$，$\therefore S_{梯形ABDC} = 5$，
$\therefore (3 + \frac{3m}{m + 6}) \times 2 \times \frac{1}{2} = 5$，$\therefore m = 12$，经检验，$m = 12$是原方程的解，$\therefore C$的坐标为$(6, 2)$。故答案为$(6, 2)$。

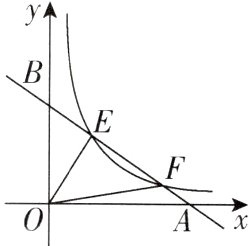
9[2024江苏盐城期末，中]如图，点E，F在函数$y=\frac{2}{x}(x＞0)$的图像上，直线EF分别与x轴、y轴交于点A，B，且点A的横坐标为4，点B的纵坐标为$\frac{8}{3}$，则△EOF的面积是________.

答案：
$\frac{8}{3}$ 【解析】如图，过$E$作$EC \perp x$轴于$C$，过$F$作$FD \perp x$轴于$D$。由题意可得，点$A$，$B$的坐标分别为$(4, 0)$，$(0, \frac{8}{3})$，则易得直线$AB$的表达式为$y = -\frac{2}{3}x + \frac{8}{3}$。联立$\begin{cases}y = -\frac{2}{3}x + \frac{8}{3} \\ y = \frac{2}{x} \end{cases}$，解得$\begin{cases}x = 1 \\ y = 2 \end{cases}$或$\begin{cases}x = 3 \\ y = \frac{2}{3} \end{cases}$，$\therefore$ 点$E$的坐标为$(1, 2)$，点$F$的坐标为$(3, \frac{2}{3})$，$\therefore CE = 2$，$DF = \frac{2}{3}$，$CD = 3 - 1 = 2$。
$\because S_{\triangle OEF} + S_{\triangle OFD} = S_{\triangle OEC} + S_{梯形ECDF}$，$S_{\triangle OFD} = S_{\triangle OEC} = \frac{1}{2} \times 2 = 1$，$\therefore S_{\triangle OEF} = S_{梯形ECDF} = \frac{1}{2}(DF + CE) \times CD = \frac{1}{2} \times (\frac{2}{3} + 2) \times 2 = \frac{8}{3}$。故答案为$\frac{8}{3}$。