《2025年初中必刷题八年级数学下册苏科版》

1[2024山东聊城质检]如图

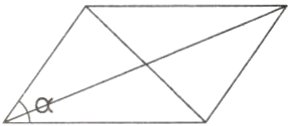
是一个平行四边形的活动框架，对角线是两根橡皮筋. 若改变框架的形状，则∠α也随之变化，两条对角线长度也发生改变. 那么当∠α = ________时，活动框架是矩形.

答案： 90°【解析】根据一个角是直角的平行四边形是矩形，可以得到∠α = 90°。

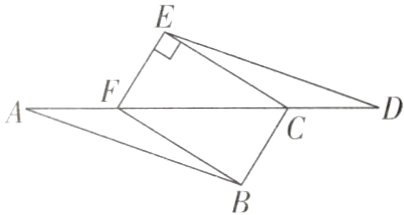
2[2024江苏常州模拟]如图，已知AB//DE，AB = DE，AC = FD，∠CEF = 90°.
(1)求证：△ABF≌△DEC；
(2)求证：四边形BCEF是矩形.

答案： 【证明】
(1)
∵AB//DE，
∴∠A = ∠D。
∵AC = FD，
∴AC - CF = DF - CF，即AF = CD。
在△ABF与△DEC中，$\begin{cases} AF = DC \\ ∠A = ∠D \\ AB = DE \end{cases}$，
∴△ABF≌△DEC(SAS)。
(2)
∵△ABF≌△DEC，
∴EC = BF，∠ECD = ∠BFA，
∴∠ECF = ∠BFC，
∴EC//BF，
∴四边形BCEF是平行四边形。
又
∵∠CEF = 90°，
∴四边形BCEF是矩形。

3如图，在Rt△ABC中，∠A = 90°，AB = 3，AC = 4，P是BC边上的一点，作PE⊥AB，PF⊥AC，垂足分别为E，F，连接EF，则EF长度的最小值是 ( )

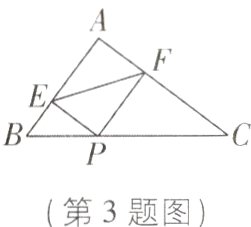
A. 2
B. 2.2
C. 2.4
D. 2.5

答案：
C【解析】连接AP，如图。
∵∠BAC = 90°，PE⊥AB，PF⊥AC，
∴∠BAC = ∠AEP = ∠AFP = 90°，
∴四边形AFPE是矩形，
∴EF = AP。要使EF长度最小，只需AP长度最小即可。当AP⊥BC时，AP长度最小。在Rt△BAC中，∠BAC = 90°，AC = 4，AB = 3，由勾股定理得BC = 5。由三角形面积公式得$\frac{1}{2}\times4\times3=\frac{1}{2}\times5\times AP$，
∴AP = 2.4，即EF长度的最小值为2.4。故选C。

4如图，在矩形ABCD中，M为AD边的中点，P为BC边上一点，PE⊥MC，PF⊥MB，当AB，BC满足条件________时，四边形PEMF为矩形.

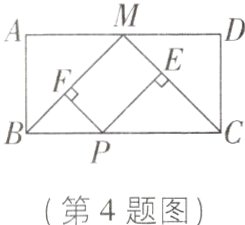
答案： $AB=\frac{1}{2}BC$【解析】当$AB=\frac{1}{2}BC$时，四边形PEMF是矩形。理由：
∵在矩形ABCD中，M为AD边的中点，$AB=\frac{1}{2}BC$，
∴AB = DC = AM = MD，∠A = ∠D = 90°，
∴∠ABM = ∠AMB = ∠DMC = ∠MCD = 45°，
∴∠BMC = 90°。又
∵PE⊥MC，PF⊥MB，
∴∠PFM = ∠PEM = 90°，
∴四边形PEMF是矩形。

5[2023广东广州越秀区调研]如图，平行四边形ABCD的四个内角的平分线分别相交于点E，F，G，H. 求证：四边形EFGH是矩形.

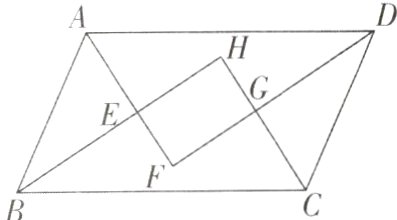
答案：
【证明】
∵四边形ABCD是平行四边形，
∴AB//CD，
∴∠ABC + ∠BCD = 180°。
技巧总结
判定矩形的常用思路：
　　　
思路分析
先由直角的个数判定四边形AFPE是矩形，再利用矩形的性质将求EF长度的最小值转化为求AP长度的最小值，最后利用垂线段最短和三角形面积公式求解即可。
易错警示
题目并未给出图形，故要注意分情况讨论，防止漏解。
∵BH，CH分别平分∠ABC，∠BCD，
∴$∠HBC=\frac{1}{2}∠ABC$，$∠HCB=\frac{1}{2}∠BCD$，
∴$∠HBC + ∠HCB=\frac{1}{2}(∠ABC + ∠BCD)=\frac{1}{2}\times180° = 90°$，
∴∠H = 90°。同理，∠HEF = ∠AEB = ∠F = 90°，
∴四边形EFGH是矩形。

6[2023江苏无锡期中]如图所示，矩形ABCD的对角线AC，BD相交于点O，E，F，G，H分别是OA，OB，OC，OD的中点，求证：四边形EFGH是矩形.

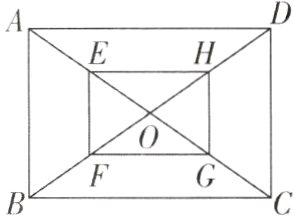
答案： 【证明】
∵E是OA的中点，G是OC的中点，
∴$OE=\frac{1}{2}AO$，$OG=\frac{1}{2}CO$。
∵四边形ABCD是矩形，
∴AO = CO，
∴OE = OG。同理可证OF = OH，
∴四边形EFGH是平行四边形。
∵$OE=\frac{1}{2}AO$，$OG=\frac{1}{2}OC$，
∴$EG = OE + OG=\frac{1}{2}AC$。同理可证，$FH=\frac{1}{2}BD$。
∵四边形ABCD是矩形，
∴AC = BD，
∴EG = FH，
∴四边形EFGH是矩形。

7[江苏连云港中考]如图，点C是BE的中点，四边形ABCD是平行四边形.
(1)求证：四边形ACED是平行四边形.
(2)如果AB = AE，求证：四边形ACED是矩形.

答案： 【证明】
(1)
∵四边形ABCD是平行四边形，
∴AD//BC，AD = BC。
∵点C是BE的中点，
∴BC = CE，
∴AD = CE。又
∵AD//CE，
∴四边形ACED是平行四边形。
(2)
∵四边形ABCD是平行四边形，
∴AB = DC。
∵AB = AE，
∴DC = AE。
∵四边形ACED是平行四边形，
∴四边形ACED是矩形。

8[2024江苏盐城质检]一种燕尾夹如图(1)所示，图(2)是在闭合状态时的示意图，图(3)是在打开状态时的示意图(数据如图，单位：mm). 则在图(3)时，点B，D之间的距离为________mm.

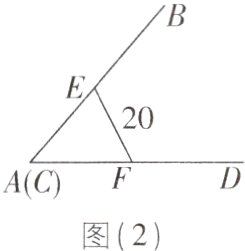
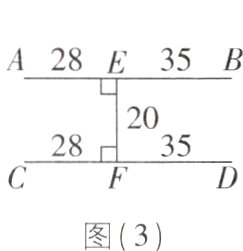
答案： 20【解析】连接BD。
∵EF⊥AB，EF⊥CD，
∴∠BEF = ∠DFE = 90°，
∴∠BEF + ∠DFE = 180°，
∴AB//CD。
∵EB = FD = 35mm，
∴四边形BDFE是平行四边形。又
∵∠BEF = 90°，
∴四边形BDFE是矩形，
∴BD = EF = 20mm。故答案为20。

9在同一平面内，设a，b，c是三条互相平行的直线，已知直线a与b之间的距离为4 cm，直线b与c之间的距离为1 cm，则直线a与c之间的距离为________cm.

答案： 5或3【解析】当直线c在直线a，b之间时，
∵a，b，c是三条互相平行的直线，直线a，b之间的距离为4cm，直线b，c之间的距离为1cm，
∴直线a，c之间的距离为4 - 1 = 3(cm)。
当直线c不在直线a，b之间时，
∵a，b，c是三条互相平行的直线，直线a，b之间的距离为4cm，直线b，c之间的距离为1cm，
∴直线a，c之间的距离为4 + 1 = 5(cm)。综上所述，直线a与c之间的距离为5cm或3cm。