《2025年初中必刷题八年级数学下册苏科版》

1[2024江苏苏州工业园区校级期中]已知反比例函数$y=\frac{k}{x}(k＜0)$，当$1\leq x\leq3$时，函数$y$的最大值和最小值之差为4，则$k$的值为 （ ）
A. -3
B. -4
C. -5
D. -6

答案： D [解析]
∵ $k ＜ 0$，
∴ 反比例函数图像位于第二、四象限，在每一象限内，$y$ 随 $x$ 的增大而增大.
∵ 当 $1\leqslant x\leqslant 3$ 时，函数 $y$ 的最大值和最小值之差为 $4$，
∴ $\frac{k}{3}-\frac{k}{1}=4$，解得 $k = - 6$. 故选 D.

2[2023江苏淮安期末]对于双曲线$y=\frac{m + 2}{x}$，在每一象限内，$y$都随$x$的增大而减小，则$m$的取值范围是 （ ）
A. $m ＞ -2$
B. $m ＜ -2$
C. $m ＞ 2$
D. $m ＜ 2$

答案： A [解析]
∵ 对于双曲线 $y=\frac{m + 2}{x}$，在每一象限内，$y$ 都随 $x$ 的增大而减小，
∴ $m + 2＞0$，
∴ $m＞-2$，
∴ $m$ 的取值范围是 $m＞-2$. 故选 A.

3[2023江苏无锡模拟]下列关于反比例函数$y=\frac{3}{x}$的描述中，正确的是 （ ）
A. 图像在第二、四象限
B. 当$x ＜ 0$时，$y$随$x$的增大而减小
C. 点$(-1,3)$在该反比例函数的图像上
D. 当$x ＜ 1$时，$y ＞ 3$

答案：
B [解析]A 反比例函数 $y = \frac{3}{x}$ 中，$k = 3＞0$，则图像在第一、三象限，故 A 错误；B 当 $x＜0$ 时，$y$ 随 $x$ 的增大而减小，故 B 正确；C 由 $( - 1)\times3=-3$ 知点 $( - 1,3)$ 不在该反比例函数的图像上，故 C 错误；D 当 $x＜0$ 时，$y＜0$；当 $0＜x＜1$ 时，$y＞3$，故 D 错误。

4[2024浙江温州模拟]已知反比例函数$y=\frac{k}{x}(k＜0)$，对于一个正数$m$，当自变量$x$满足$m\leq x\leq2m$时，函数$y$的最大值为$a$，则当$-2m\leq x\leq -m$时，函数$y$有 （ ）
A. 最大值$-2a$
B. 最小值$-2a$
C. 最大值$-a$
D. 最小值$-\frac{1}{2}a$

答案： A [解析]
∵ 反比例函数 $y=\frac{k}{x}(k ＜ 0)$，
∴ 函数图像位于第二、四象限，在每个象限内，$y$ 随 $x$ 的增大而增大.
∵ 对于一个正数 $m$，当自变量 $x$ 满足 $m\leqslant x\leqslant 2m$ 时，函数 $y$ 的最大值为 $a$，
∴ $\frac{k}{2m}=a$，
∴ $k = 2ma$，
∴ $y=\frac{2ma}{x}$.
∵ $-2m\leqslant x\leqslant - m$，
∴ 当 $x=-2m$ 时，函数 $y$ 有最小值 $\frac{2ma}{-2m}=-a$，当 $x=-m$ 时，函数 $y$ 有最大值 $\frac{2ma}{-m}=-2a$. 故选 A.

5[2024重庆万州区调研]在反比例函数$y=\frac{2024 - k}{x}$的图像上有两点$A(x_1,y_1)$，$B(x_2,y_2)$，当$x_1 ＜ 0 ＜ x_2$时，有$y_1 ＜ y_2$，则$k$的取值范围是________.

答案： $k＜2024$ [解析]
∵ 当 $x_1＜0＜x_2$ 时，$y_1＜y_2$，
∴ 反比例函数图像位于第一、三象限，
∴ $2024 - k＞0$，解得 $k＜2024$. 故答案为 $k＜2024$.

6[2023江苏盐城期末]反比例函数$y=\frac{1}{x}$的图像上有三个点$(x_1,y_1)$，$(x_2,y_2)$，$(x_3,y_3)$，若$x_1 ＜ x_2 ＜ 0 ＜ x_3$，则$y_1$，$y_2$，$y_3$的大小关系是________.

答案： $y_2＜y_1＜y_3$ [解析]
∵ 反比例函数 $y=\frac{1}{x}$ 的图像在第一、三象限，且在每一个象限内，$y$ 随 $x$ 的增大而减小，点 $(x_1,y_1)$，$(x_2,y_2)$，$(x_3,y_3)$ 在反比例函数 $y=\frac{1}{x}$ 的图像上，且 $x_1＜x_2＜0＜x_3$，
∴ 点 $(x_1,y_1)$，$(x_2,y_2)$ 在第三象限，$y_2＜y_1＜0$，点 $(x_3,y_3)$ 在第一象限，$y_3＞0$，
∴ $y_2＜y_1＜y_3$，故答案为 $y_2＜y_1＜y_3$.

7[2024江苏盐城东台期中]若下列图中双曲线的表达式均为$y=\frac{6}{x}$，则阴影部分的面积为3的是 （ ）

答案： A [解析]A 选项，阴影部分面积为 $\frac{1}{2}k = 3$，故符合题意；B 选项，阴影部分面积为 $k = 6$，故不符合题意；C 选项，阴影部分面积为 $2\times\frac{1}{2}k=2\times\frac{1}{2}\times6 = 6$，故不符合题意；D 选项，阴影部分面积为 $4\times\frac{1}{2}k=4\times\frac{1}{2}\times6 = 12$，故不符合题意.

8[2023江苏徐州铜山区期末]如图，两个反比例函数$y=\frac{4}{x}$和$y=\frac{2}{x}$在第一象限的图像分别是$C_1$和$C_2$，设点$P$在$C_1$上，$PA\perp x$轴于点$A$，交$C_2$于点$B$，则$\triangle POB$的面积为 （ ）

A. 1
B. 2
C. 3
D. 4

答案：
A
识图解题 两条双曲线的 $k$ 值符号相同时，求阴影部分面积的基本模型
$S_{矩形 OFAB}=S_{矩形 OECC_1}=\vert k_1\vert$
$S_{阴影}=S_{\triangle AOB}-S_{\triangle AOD}=\frac{1}{2}\vert k_1\vert-\frac{1}{2}\vert k_2\vert$
$S_{阴影}=S_{\triangle COB}-S_{\triangle OCE}=\frac{1}{2}\vert k_1\vert-\frac{1}{2}\vert k_2\vert$

$S_{阴影}=S_{矩形 ABC}-S_{\triangle OCE}-S_{\triangle OAD}=\vert k_1\vert-\vert k_2\vert$
[解析]
∵ $PA\perp x$ 轴于点 $A$，交 $C_2$ 于点 $B$，
∴ $S_{\triangle POA}=\frac{1}{2}\times4 = 2$，$S_{\triangle BOA}=\frac{1}{2}\times2 = 1$，
∴ $S_{\triangle POB}=2 - 1 = 1$. 故选 A.

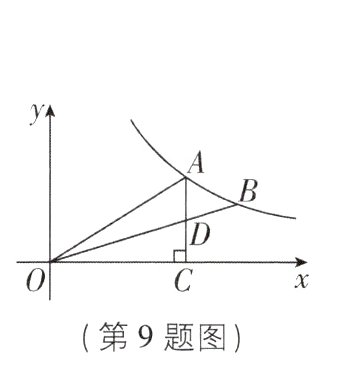
9如图，$A$，$B$是双曲线$y=\frac{k}{x}(x ＞ 0)$上的两点，连接$OA$，$OB$. 过点$A$作$AC\perp x$轴于点$C$，交$OB$于点$D$. 若$D$为$AC$的中点，$\triangle AOD$的面积为3，点$B$的坐标为$(m,2)$，则$m$的值为________.

答案： 6 [解析]因为 $D$ 为 $AC$ 的中点，$\triangle AOD$ 的面积为 $3$，所以 $\triangle AOC$ 的面积为 $6$，所以 $k = 12 = 2m$，解得 $m = 6$. 故答案为 $6$.

10在函数$y=\frac{-k^2 - 3}{x}$（$k$为常数）的图像上有$A(-5,y_1)$，$B(-1,y_2)$，$C(4,y_3)$三点，则函数值$y_1$，$y_2$，$y_3$的大小关系是 （ ）
A. $y_3 ＜ y_2 ＜ y_1$
B. $y_2 ＜ y_3 ＜ y_1$
C. $y_1 ＜ y_2 ＜ y_3$
D. $y_3 ＜ y_1 ＜ y_2$

答案： D [解析]
∵ $-k^2 - 3＜0$，
∴ 函数 $y=\frac{-k^2 - 3}{x}(k$ 为常数 $)$ 的图像在第二、四象限.
∵ 点 $C(4,y_3)$ 的横坐标 $4＞0$，
∴ 点 $C$ 在第四象限，$y_3＜0$.
∵ 点 $A(-5,y_1)$，$B(-1,y_2)$ 的横坐标 $-5＜-1＜0$，
∴ $y_1＞0$，$y_2＞0$.
∵ 函数图像在第二象限内，$y$ 随 $x$ 的增大而增大，
∴ $0＜y_1＜y_2$，
∴ $y_3＜y_1＜y_2$. 故选 D.

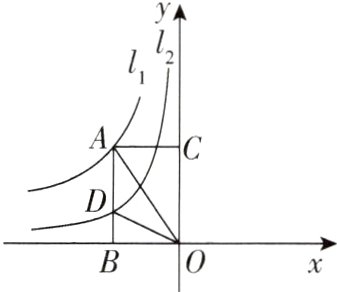
1[2024河北沧州期中，中]双曲线$l_1:y=-\frac{6}{x}(x ＜ 0)$和$l_2:y=\frac{k}{x}(k\neq0,x ＜ 0)$的图像如图所示，点$A$是$l_1$上一点，分别过点$A$作$AB\perp x$轴，$AC\perp y$轴，垂足分别为点$B$，点$C$，$AB$与$l_2$交于点$D$，若$\triangle AOD$的面积为2，则$k$的值为 （ ）

A. 4
B. -4
C. 2
D. -2

答案： D [解析]
∵ 点 $A$ 在反比例函数 $y = -\frac{6}{x}(x＜0)$ 的图像上，$AB\perp x$ 轴，
∴ $S_{\triangle ABO}=\frac{1}{2}\times\vert - 6\vert = 3$.
∵ $S_{\triangle AOD}=2$，
∴ $S_{\triangle BOD}=S_{\triangle ABO}-S_{\triangle ADO}=3 - 2 = 1$.
∵ 点 $D$ 在 $l_2$ 上，
∴ $\vert k\vert = 2S_{\triangle BOD}=2$.
∵ 反比例函数 $y=\frac{k}{x}(k\neq0,x＜0)$ 的图像位于第二象限，
∴ $k=-2$. 故选 D.