《2025年初中必刷题八年级数学下册苏科版》

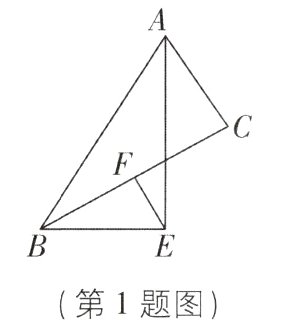
1. [2023江苏苏州质检，中]如图，在△ABC中，AE 平分∠BAC，BE⊥AE于点E，点F是BC的中点. 若AB = 10，AC = 6，则EF的长为（　　　）

A. 2　　　
　B. 3　　　
　C. 4　　　
　D. 5

答案：
A
添加辅助线
由“AE平分∠BAC，BE⊥AE”联想到等腰三角形的“三线合一”，而图形中与之相关的三角形并不完整，于是考虑把相关的三角形补充完整，分别延长AC，BE交于点M，则可打开问题突破口。
【解析】如图，延长AC，BE交于点M。

∵ AE平分∠CAB，AE⊥BE，
∴ ∠AEB = ∠AEM = 90°，∠CAE = ∠BAE，AB = AM = 10，BE = EM。
∵ AC = 6，
∴ CM = AM - AC = 10 - 6 = 4。
∵ 点F是BC的中点，BE = EM，
∴ EF为△BCM的中位线，
∴ EF = $\frac{1}{2}CM = 2$。故选A。

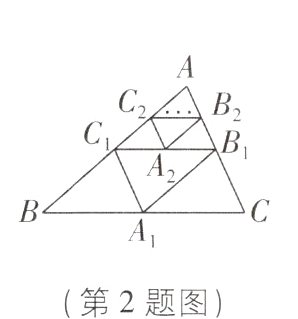
2. [中]如图，△ABC的周长为a，以它各边的中点为顶点作△A₁B₁C₁，再以△A₁B₁C₁各边的中点为顶点作△A₂B₂C₂，…，如此下去，则△AₙBₙCₙ的周长为（　　　）

A. $\frac{1}{2^{n}}a$　　
　B. $\frac{1}{3^{n}}a$　　
　C. $\frac{1}{2^{n - 1}}a$　
　D. $\frac{1}{3^{n - 1}}a$

答案： A【解析】
∵ 点$A_1$，$B_1$，$C_1$分别为BC，AC，AB的中点，
∴ $B_1C_1=\frac{1}{2}BC$，$A_1C_1=\frac{1}{2}AC$，$A_1B_1=\frac{1}{2}AB$，
∴ △$A_1B_1C_1$的周长为$\frac{1}{2}a$，同理△$A_2B_2C_2$的周长为$\frac{1}{4}a=\frac{1}{2^{2}}a$，…，则△$A_nB_nC_n$的周长为$\frac{1}{2^{n}}a$，故选A。

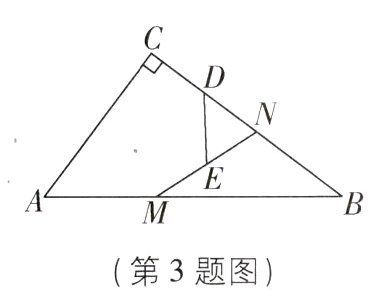
3. [2024江苏盐城东台期中，中]在Rt△ABC中，∠C = 90°，AC = 6，BC = 8，点N是BC边上一点. 点M为AB边上的动点（不与点B重合），点D，E分别为CN，MN的中点，则DE的取值范围为（　　　）

A. 3＜DE＜4　　　　　　
　B. 3≤DE＜4
C. 3≤DE≤4　　　　　
　D. $\frac{12}{5}$≤DE＜4

答案： D【解析】连接CM。
∵ ∠ACB = 90°，AC = 6，BC = 8，
∴ $AB=\sqrt{AC^{2}+BC^{2}} = 10$。
∵ 点D，E分别为CN，MN的中点，
∴ $DE=\frac{1}{2}CM$，
∴ 当CM最小时，DE最小。当CM⊥AB时，CM取最小值，
∴ $S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}AB\cdot CM$，
∴ $CM=\frac{AC\cdot BC}{AB}=\frac{24}{5}$，
∴ $DE=\frac{1}{2}CM=\frac{12}{5}$，即DE的最小值为$\frac{12}{5}$。
∵ CM ＜ BC，
∴ CM ＜ 8，
∴ DE ＜ 4，
∴ $\frac{12}{5}\leq DE ＜ 4$。

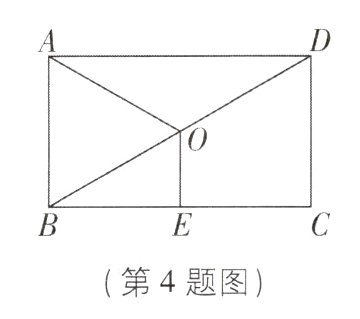
4. [2023江苏南京鼓楼区调研，中]如图，点O是□ABCD的对角线BD的中点，点E是BC的中点，连接OA，OE. 若∠C = 90°，OA = 2，OE = 1，则△BOE的周长为__________.

答案： $\sqrt{3}+3$【解析】在□ABCD中，∠C = 90°，
∴ 四边形ABCD是矩形。
∵ O是BD的中点，
∴ OA = OB = 2。连接OC，则OC = OB。
∵ E是BC的中点，
∴ OE是△BCD的中位线，
∴ OE//CD，
∴ ∠BEO = ∠BCD = 90°。在Rt△BOE中，由勾股定理，得$BE=\sqrt{3}$，则△BOE的周长为$BE + OE + OB=\sqrt{3}+3$。故答案为$\sqrt{3}+3$。

5. [中]如图，△ABC的周长为28，点D，E都在边BC 上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB 的平分线垂直于AD，垂足为P. 若BC = 10，则PQ 的长是________.

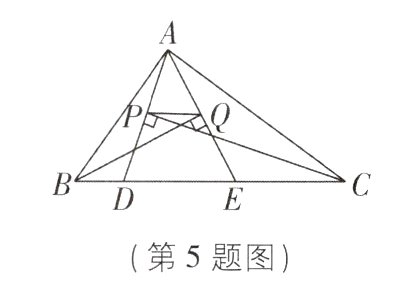
答案： 4【解析】
∵ △ABC的周长是28，BC = 10，
∴ AB + AC = 28 - 10 = 18。
∵ ∠ABC的平分线垂直于AE，
∴ ∠AQB = ∠EQB = 90°，∠ABQ = ∠EBQ。在△ABQ和△EBQ中，$\begin{cases}∠ABQ = ∠EBQ \\ BQ = BQ \\ ∠AQB = ∠EQB\end{cases}$，
∴ △ABQ≌△EBQ（ASA），
∴ AQ = EQ，AB = BE。同理可证AP = DP，AC = CD，
∴ DE = BE + CD - BC = AB + AC - BC = 18 - 10 = 8。
∵ AQ = EQ，AP = DP，
∴ PQ是△ADE的中位线，
∴ $PQ=\frac{1}{2}DE = 4$。故答案为4。

6. [2023辽宁本溪模拟，中]如图，在△ABC中，∠A = 90°，AC＞AB＞4，点D，E分别在边AB，AC上，BD = 4，CE = 3，取DE，BC 的中点M，N，则线段MN的长为__________.

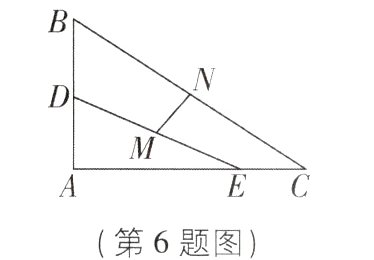
答案：
2.5【解析】如图，作CH//AB，连接DN并延长交CH于H，连接EH。
∵ AB//CH，
∴ ∠B = ∠NCH，∠ECH + ∠A = 180°。
∵ ∠A = 90°，

∴ ∠ECH = ∠A = 90°。
∵ N是BC的中点，
∴ BN = CN。在△DNB和△HNC中，$\begin{cases}∠B = ∠NCH \\ BN = CN \\ ∠DNB = ∠HNC\end{cases}$，
∴ △DNB≌△HNC（ASA），
∴ CH = BD = 4，DN = NH。在Rt△CEH中，
∵ CH = 4，CE = 3，
∴ $EH=\sqrt{CH^{2}+CE^{2}}=\sqrt{4^{2}+3^{2}} = 5$。
∵ M是DE的中点，
∴ DM = ME，
∴ $MN=\frac{1}{2}EH = 2.5$，故答案为2.5。

7. [2023江苏苏州工业园区一模，较难]如图，在△ABC中，∠C = 90°，AC = 4，BC = 3，将△ABC绕点B 旋转得△A′BC′，连接AA′，分别取AA′，BC′的中点E，F，连接AC′，EF，则EF的取值范围是__________.

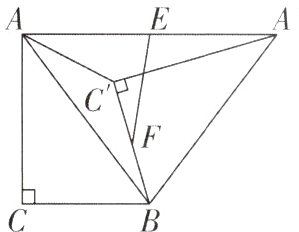
答案：
$\frac{1}{2}\leq EF\leq\frac{9}{2}$【解析】如图，取$A'B$的中点G，连接EG，FG。

∵ ∠C = 90°，AC = 4，BC = 3，
∴ $AB=\sqrt{3^{2}+4^{2}} = 5$。由旋转的性质可知，$A'C' = AC = 4$，$A'B = AB = 5$，$BC' = BC = 3$。
∵ 点E，F，G分别是$AA'$，$BC'$，$A'B$的中点，
∴ EG是△$A'AB$的中位线，FG是△$BC'A'$的中位线，
∴ $EG=\frac{1}{2}AB=\frac{5}{2}$，$FG=\frac{1}{2}A'C' = 2$。当点E，F，G不共线时，EG - FG ＜ EF ＜ EG + FG，即$\frac{1}{2}＜EF＜\frac{9}{2}$。当点G在线段EF上时，$EF = EG + FG=\frac{5}{2}+2=\frac{9}{2}$，当点F在线段EG上时，$EF = EG - FG=\frac{5}{2}-2=\frac{1}{2}$。综上所述，$\frac{1}{2}\leq EF\leq\frac{9}{2}$，故答案为$\frac{1}{2}\leq EF\leq\frac{9}{2}$。

8. 核心素养 推理能力 [较难]在△ABC中，AC＞BC，D为AB的中点，E为线段AC上的一点.
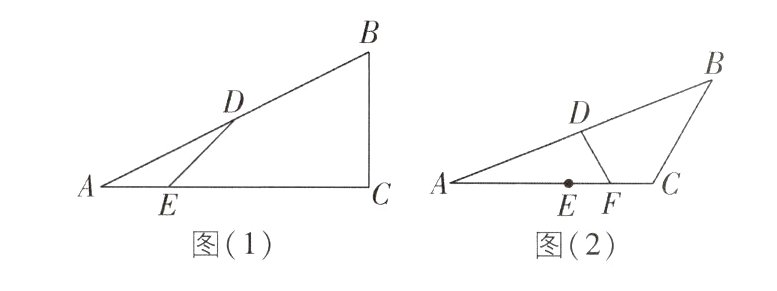
（1）如图（1），若AE = $\frac{1}{4}$AC，∠C = 90°，BC = 2，AC = 4，求DE的长；
（2）如图（2），若AE = BC，且F为EC的中点，求证：∠AFD = $\frac{1}{2}$∠C；
（3）若2∠AED - ∠C = 180°，试探究AE，BC，AC之间的数量关系，并证明.

答案：
（1）【解】取AC的中点G，连接DG，如图（1）。
∵ D为AB的中点，
∴ DG为△ACB的中位线，
∴ DG//BC，DG = $\frac{1}{2}BC = 1$，$AG = CG=\frac{1}{2}AC = 2$，
∴ ∠AGD = ∠C = 90°。
∵ $AE=\frac{1}{4}AC$，
∴ AE = EG = 1。在Rt△DGE中，$DE=\sqrt{1^{2}+1^{2}}=\sqrt{2}$。

关键点拨
利用勾股定理求出AB的长，再根据旋转的性质可得$A'C' = AC = 4$，$A'B = AB = 5$，$BC' = BC = 3$，利用中位线的性质可得$EG=\frac{5}{2}$，$FG = 2$，进而可求解。
关键点拨
由菱形的性质可知点B关于AC的对称点为D，连接ED，交AC于G，则BG = DG，当D，G，E三点共线时，BG + EG最小。
（2）【证明】连接BE，取BE中点M，连接MF，MD，如图（2）。
∵ F为EC的中点，D为AB的中点，
∴ MF//BC且$MF=\frac{1}{2}BC$，MD//AE且$MD=\frac{1}{2}AE$。
∵ AE = BC，
∴ MD = MF，
∴ ∠MDF = ∠MFD。又
∵ MD//AE，
∴ ∠AFD = ∠MDF，
∴ ∠AFD = $\frac{1}{2}∠AFM$。
∵ MF//BC，
∴ ∠AFM = ∠C，
∴ $∠AFD=\frac{1}{2}∠C$。
（3）【解】AC = 2AE + BC。
证明：在EC上截取EM，使得EM = AE，连接BM，作CH⊥BM于H，如图（3）。

∵ AE = EM，AD = DB，
∴ ED为△ABM的中位线，
∴ DE//BM，
∴ ∠AED = ∠AMB = ∠MHC + ∠MCH = 90° + ∠MCH。
∵ 2∠AED - ∠ACB = 180°，
∴ ∠AED = 90° + $\frac{1}{2}∠ACB$，
∴ $∠MCH=\frac{1}{2}∠ACB$，
∴ ∠MCH = ∠BCH。又
∵ CH = CH，∠CHM = ∠CHB = 90°，
∴ △CHM≌△CHB，
∴ BC = MC，
∴ AC = 2AE + BC。