《2025年初中必刷题八年级数学下册苏科版》

1 [2024江苏扬州邗江区期中,中]固体糖溶于水可得到糖水.现有甲、乙、丙、丁四瓶糖水，如图，x轴表示糖水质量，y轴表示含糖浓度(含糖浓度:瓶中固体糖质量与糖水质量的比值)，其中描述甲、丁的两点恰好在同一个反比例函数的图像上，则这四瓶糖水中含固体糖质量最多的是(　　)
　　　　　　
A. 甲　　　
　B. 乙　　
　C. 丙　　
　D. 丁

答案： B【解析】根据题意，可知$xy$的值即为糖水中含固体糖质量.$\because$描述甲、丁的两点恰好在同一个反比例函数的图像上，$\therefore$甲、丁两瓶糖水中含固体糖质量相同.$\because$点乙在反比例函数图像上面，点丙在反比例函数图像下面，$\therefore$乙瓶中，$xy$的值最大，即糖水中含固体糖质量最多，丙瓶中，$xy$的值最小，即糖水中含固体糖质量最少.

2 [中]为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x 之间的变化如图所示，治污完成前是反比例函数图像的一部分,治污完成后是一次函数图像的一部分,下列选项错误的是(　　)
　　　　　　
A. 4月份的利润为50万元
B. 治污改造完成后每月利润比前一个月增加30万元
C. 治污改造完成前后共有4个月的利润低于100万元
D. 9月份该厂利润达到200万元

答案： C【解析】A选项，设反比例函数的表达式为$y = \frac{k}{x}$. 把$(1,200)$代入得$k = 200$，$\therefore$反比例函数的表达式为$y = \frac{200}{x}(1\leq x ＜ 4)$. 当$x = 4$时，$y = 50$，$\therefore 4$月份的利润为$50$万元，故此选项正确，不合题意. B选项，治污改造完成后，从$4$月到$6$月，利润从$50$万元增长到$110$万元，故每月利润比前一个月增加$30$万元，故此选项正确，不合题意. C选项，当$1\leq x ＜ 4$时，有$100 = \frac{200}{x}$，解得$x = 2$；当$x\geq4$时，$5$月份利润为$50 + 30 = 80$(万元)$＜ 100$万元，$\therefore$只有$3$月，$4$月，$5$月共$3$个月的利润低于$100$万元，故此选项不正确，符合题意. D选项，设一次函数表达式为$y = mx + b$，则$\begin{cases}4m + b = 50\\6m + b = 110\end{cases}$，解得$\begin{cases}m = 30\\b = -70\end{cases}$，$\therefore$一次函数表达式为$y = 30x - 70(x\geq4)$. 当$y = 200$时，$200 = 30x - 70$，解得$x = 9$，即$9$月份该厂利润达到$200$万元，故此选项正确，不合题意. 故选C.

3 [2024福建泉州模拟,中]某气球内充满了一定质量的气体,当温度不变时，气球内气体的气压p(千帕)是气球的体积V(立方米)的反比例函数,其图像如图所示.(千帕是一种压强单位)
　(1)求这个函数的表达式;
　(2)当气球的体积为1.2立方米时,气球内的气压是多少千帕？
　(3)当气球内的气压大于160千帕时,气球将爆炸,为了安全起见,求气球的体积应控制的范围.
　　　　　　　　　　　　

答案： 【解】
(1)设$p = \frac{k}{V}(V ＞ 0)$.
将$(2,48)$代入得，$k = 96$，
$\therefore p = \frac{96}{V}(V ＞ 0)$.
(2)当$V = 1.2$时，$p = \frac{96}{1.2} = 80$，
$\therefore$气球内的气压是$80$千帕.
(3)当$p = 160$时，$V = \frac{96}{160} = 0.6$.
$\because$当$V ＞ 0$时，$p$随$V$的增大而减小，
$\therefore$当$p\leq160$时，$V\geq0.6$，
$\therefore$为了安全起见，气球的体积应不小于$0.6$立方米.

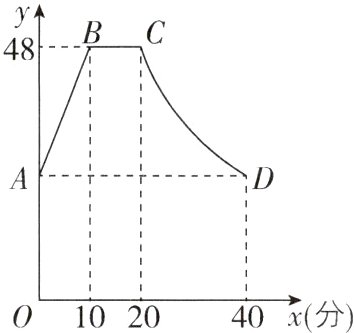
4 [2023江苏常州期末,较难]实验研究发现:学生在数学课上的听课注意力指标y随上课时间x(分)的变化而变化,上课开始时,学生的注意力指标激增,中间一段时间,学生的注意力指标保持平稳状态，随后注意力开始分散.学生的注意力指标y随时间x(分)变化的函数图像如图所示，当$0\leq x＜10$和$10\leq x＜20$时,图像是线段;当$20\leq x\leq40$时,图像是反比例函数图像的一部分.
　(1)求点A对应的指标值;
　(2)张老师在一节课上讲解一道数学综合题需要15分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标都不低于32？请说明理由.
　　　　　　　　　　　

答案： 【解】
(1)设当$20\leq x\leq40$时，反比例函数的表达式为$y = \frac{k}{x}$. 将$C(20,48)$代入得$48 = \frac{k}{20}$，解得$k = 960$，$\therefore$反比例函数的表达式为$y = \frac{960}{x}(20\leq x\leq40)$. 当$x = 40$时，$y = \frac{960}{40} = 24$，$\therefore D(40,24)$，$\therefore A(0,24)$，即$A$对应的指标值为$24$.
(2)张老师能经过适当的安排，使学生在听这道综合题的讲解时，注意力指标都不低于$32$.
理由如下：设当$0\leq x ＜ 10$时，$AB$所在直线的表达式为$y = mx + n$. 将$A(0,24)$，$B(10,48)$代入得$\begin{cases}24 = n\\48 = 10m + n\end{cases}$，解得$\begin{cases}m = \frac{12}{5}\\n = 24\end{cases}$，$\therefore AB$所在直线的表达式为$y = \frac{12}{5}x + 24$. 当$y\geq32$时，$\frac{12}{5}x + 24\geq32$，解得$x\geq\frac{10}{3}$. 由
(1)得反比例函数的表达式为$y = \frac{960}{x}$，当$y\geq32$时，$\frac{960}{x}\geq32$，解得$x\leq30$，$\therefore\frac{10}{3}\leq x\leq30$时，注意力指标都不低于$32$，而$30 - \frac{10}{3} = \frac{80}{3} ＞ 15$，$\therefore$张老师能经过适当的安排，使学生在听这道综合题的讲解时，注意力指标都不低于$32$.
关键点拔：
(1)熟练掌握用待定系数法求反比例函数和一次函数表达式是解题关键.
思路分析：
(1)设反比例函数的表达式为$y = \frac{k}{x}$，由$C(20,48)$求出$k$，可得$D$的坐标，从而求出$A$对应的指标值；
(2)求出$AB$所在直线的表达式，得到$y\geq32$时，$x\geq\frac{10}{3}$，由反比例函数$y = \frac{960}{x}$，可得$y\geq32$时，$x\leq30$，根据$30 - \frac{10}{3} = \frac{80}{3} ＞ 15$，即可得到答案.