第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
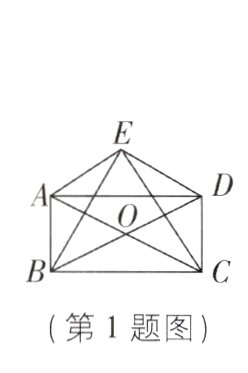
1[中]如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE,DE,BE⊥DE,AC,BD相交于点O且互相平分. 若2AB = BC = 2,则BD的长为 ( )
A. $\sqrt{20}$
B. $\sqrt{5}$
C. 3
D. 4

A. $\sqrt{20}$
B. $\sqrt{5}$
C. 3
D. 4
答案:
B【解析】连接OE。
∵2AB = BC = 2,
∴AB = 1。
∵AC,BD互相平分,
∴OA = OC,OB = OD,
∴四边形ABCD是平行四边形。
∵以AC为斜边作Rt△ACE,
∴$OE = OA = OC=\frac{1}{2}AC$。
∵BE⊥DE,
∴$OE = OB = OD=\frac{1}{2}BD$,
∴AC = BD,
∴四边形ABCD是矩形,
∴AD = BC = 2,∠BAD = 90°,
∴$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,故选B。
∵2AB = BC = 2,
∴AB = 1。
∵AC,BD互相平分,
∴OA = OC,OB = OD,
∴四边形ABCD是平行四边形。
∵以AC为斜边作Rt△ACE,
∴$OE = OA = OC=\frac{1}{2}AC$。
∵BE⊥DE,
∴$OE = OB = OD=\frac{1}{2}BD$,
∴AC = BD,
∴四边形ABCD是矩形,
∴AD = BC = 2,∠BAD = 90°,
∴$BD=\sqrt{AB^{2}+AD^{2}}=\sqrt{1^{2}+2^{2}}=\sqrt{5}$,故选B。
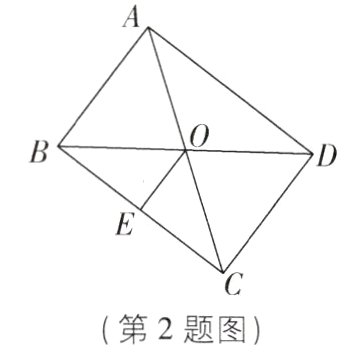
2[2024江苏宿迁期中,中]如图,在□ABCD中,AB = $\sqrt{2}$,AD = 2,连接AC,BD相交于点O,E为BC的中点,若BD = $\sqrt{6}$,则四边形OECD的面积为 ( )
A. $\frac{\sqrt{2}}{2}$
B. $\frac{3\sqrt{2}}{2}$
C. $\frac{3\sqrt{2}}{4}$
D. $\frac{3\sqrt{3}}{2}$

A. $\frac{\sqrt{2}}{2}$
B. $\frac{3\sqrt{2}}{2}$
C. $\frac{3\sqrt{2}}{4}$
D. $\frac{3\sqrt{3}}{2}$
答案:
C【解析】
∵$AB=\sqrt{2}$,AD = 2,$BD=\sqrt{6}$,
∴$AB^{2}+AD^{2}=2 + 4 = 6$,$BD^{2}=6$,
∴$AB^{2}+AD^{2}=BD^{2}$,
∴∠BAD = 90°,
∴□ABCD是矩形,
∴$S_{\triangle BOC}=S_{\triangle DOC}=\frac{1}{4}S_{矩形ABCD}$。
∵E为BC的中点,
∴BE = EC,
∴$S_{\triangle OEC}=\frac{1}{2}S_{\triangle BOC}$,
∴四边形OECD的面积为$S_{\triangle OCD}+\frac{1}{2}S_{\triangle OCD}=\frac{1}{4}S_{矩形ABCD}+\frac{1}{8}S_{矩形ABCD}=\frac{3}{8}S_{矩形ABCD}=\frac{3}{8}\times AB\times AD=\frac{3}{8}\times2\times\sqrt{2}=\frac{3\sqrt{2}}{4}$。故选C。
∵$AB=\sqrt{2}$,AD = 2,$BD=\sqrt{6}$,
∴$AB^{2}+AD^{2}=2 + 4 = 6$,$BD^{2}=6$,
∴$AB^{2}+AD^{2}=BD^{2}$,
∴∠BAD = 90°,
∴□ABCD是矩形,
∴$S_{\triangle BOC}=S_{\triangle DOC}=\frac{1}{4}S_{矩形ABCD}$。
∵E为BC的中点,
∴BE = EC,
∴$S_{\triangle OEC}=\frac{1}{2}S_{\triangle BOC}$,
∴四边形OECD的面积为$S_{\triangle OCD}+\frac{1}{2}S_{\triangle OCD}=\frac{1}{4}S_{矩形ABCD}+\frac{1}{8}S_{矩形ABCD}=\frac{3}{8}S_{矩形ABCD}=\frac{3}{8}\times AB\times AD=\frac{3}{8}\times2\times\sqrt{2}=\frac{3\sqrt{2}}{4}$。故选C。
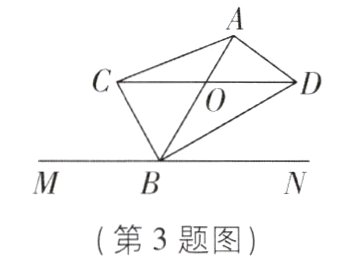
3[中]如图,线段AB的端点B在直线MN上,过线段AB上的一点O作MN的平行线,分别交∠ABM和∠ABN的平分线于点C,D,连接AC,AD. 添加一个适当的条件:当________时,四边形ACBD为矩形.

答案:
O是AB的中点(答案不唯一)【解析】添加条件为O是AB的中点。理由如下:
∵CD//MN,
∴∠OCB = ∠CBM。
∵BC平分∠ABM,
∴∠OBC = ∠CBM,
∴∠OCB = ∠OBC,
∴OC = OB。同理可证OB = OD,
∴OB = OC = OD。当O是AB的中点时,OA = OB,
∴OA = OB = OC = OD,
∴四边形ACBD是平行四边形。
∵CD = OC + OD,AB = OA + OB,
∴AB = CD,
∴平行四边形ACBD是矩形。故答案为O是AB的中点(答案不唯一)。
∵CD//MN,
∴∠OCB = ∠CBM。
∵BC平分∠ABM,
∴∠OBC = ∠CBM,
∴∠OCB = ∠OBC,
∴OC = OB。同理可证OB = OD,
∴OB = OC = OD。当O是AB的中点时,OA = OB,
∴OA = OB = OC = OD,
∴四边形ACBD是平行四边形。
∵CD = OC + OD,AB = OA + OB,
∴AB = CD,
∴平行四边形ACBD是矩形。故答案为O是AB的中点(答案不唯一)。
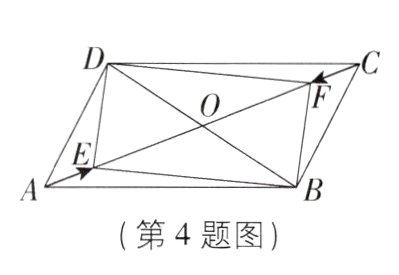
4[2024江苏南京玄武区期中,中]如图,在平行四边形ABCD中,对角线AC,BD相交于点O,动点E以每秒1个单位长度的速度从点A出发沿AC方向运动,点F同时以每秒1个单位长度的速度从点C出发沿CA方向运动. 若AC = 12,BD = 8,则经过________秒后,四边形BEDF是矩形.

答案:
2或10【解析】设运动的时间为t秒。
∵四边形ABCD是平行四边形,AC = 12,BD = 8,
∴$OA = OC=\frac{1}{2}AC = 6$,$OB = OD=\frac{1}{2}BD = 4$。
∵AE = CF = t,
∴OE = OF = 6 - t或OE = OF = t - 6,
∴四边形BEDF是平行四边形,
∴当EF = BD时,四边形BEDF是矩形,
∴OE = OD,
∴6 - t = 4或t - 6 = 4,
∴t = 2或t = 10,
∴经过2秒或10秒后,四边形BEDF是矩形。
∵四边形ABCD是平行四边形,AC = 12,BD = 8,
∴$OA = OC=\frac{1}{2}AC = 6$,$OB = OD=\frac{1}{2}BD = 4$。
∵AE = CF = t,
∴OE = OF = 6 - t或OE = OF = t - 6,
∴四边形BEDF是平行四边形,
∴当EF = BD时,四边形BEDF是矩形,
∴OE = OD,
∴6 - t = 4或t - 6 = 4,
∴t = 2或t = 10,
∴经过2秒或10秒后,四边形BEDF是矩形。
5[2023江苏南京鼓楼区期中,中]如图,在四边形ABCD中,∠A = 60°,∠ABC = ∠ADC = 90°,BC = 1,CD = 10,过D作DH⊥AB于H,则DH的长是________.
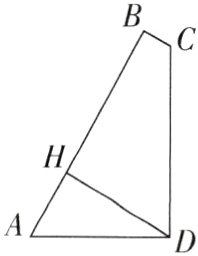

答案:
6
思路分析
注意到条件中的∠ABC = ∠ADC = ∠DHB = 90°,则考虑过C作CE⊥DH于E,构造矩形BCEH,得HE = BC = 1,再推导出∠DCE = 30°,用含30°角的直角三角形的性质求得DE,即可求出DH的长。
【解析】如图,过C作CE⊥DH于E,则∠CEH = ∠CED = 90°。
∵DH⊥AB,
∴∠AHD = ∠BHE = 90°。
∵∠ABC = 90°,
∴四边形BCEH是矩形,
∴HE = BC = 1。
∵∠ABC = ∠ADC = 90°,∠A = 60°,
∴∠BCD = 360° - 90° - 90° - 60° = 120°,
∴∠DCE = 120° - ∠BCE = 30°,

∴$DE=\frac{1}{2}CD = 5$,
∴DH = HE + DE = 6。
6
思路分析
注意到条件中的∠ABC = ∠ADC = ∠DHB = 90°,则考虑过C作CE⊥DH于E,构造矩形BCEH,得HE = BC = 1,再推导出∠DCE = 30°,用含30°角的直角三角形的性质求得DE,即可求出DH的长。
【解析】如图,过C作CE⊥DH于E,则∠CEH = ∠CED = 90°。
∵DH⊥AB,
∴∠AHD = ∠BHE = 90°。
∵∠ABC = 90°,
∴四边形BCEH是矩形,
∴HE = BC = 1。
∵∠ABC = ∠ADC = 90°,∠A = 60°,
∴∠BCD = 360° - 90° - 90° - 60° = 120°,
∴∠DCE = 120° - ∠BCE = 30°,

∴$DE=\frac{1}{2}CD = 5$,
∴DH = HE + DE = 6。
6[2023江苏常州质检,中]如图,在□ABCD中,对角线AC与BD相交于点O,点E,F分别为OB,OD的中点,延长AE至G,使EG = AE,连接CG.
(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.

(1)求证:△ABE≌△CDF;
(2)当AB与AC满足什么数量关系时,四边形EGCF是矩形?请说明理由.

答案:
(1)【证明】
∵四边形ABCD是平行四边形,
∴AB = CD,AB//CD,OB = OD,OA = OC,
∴∠ABE = ∠CDF。
∵点E,F分别为OB,OD的中点,
∴$BE=\frac{1}{2}OB$,$DF=\frac{1}{2}OD$,
∴BE = DF。在△ABE和△CDF中,$\begin{cases} AB = CD \\ ∠ABE = ∠CDF \\ BE = DF \end{cases}$,
∴△ABE≌△CDF(SAS)。
(2)【解】当AC = 2AB时,四边形EGCF是矩形。理由如下:
∵AC = 2OA,AC = 2AB,
∴AB = OA。
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG = 90°。同理,CF⊥OD,
∴EG//CF。由
(1)得△ABE≌△CDF,
∴AE = CF。
∵EG = AE,
∴EG = CF,
∴四边形EGCF是平行四边形。
∵∠OEG = 90°,
∴四边形EGCF是矩形。
(1)【证明】
∵四边形ABCD是平行四边形,
∴AB = CD,AB//CD,OB = OD,OA = OC,
∴∠ABE = ∠CDF。
∵点E,F分别为OB,OD的中点,
∴$BE=\frac{1}{2}OB$,$DF=\frac{1}{2}OD$,
∴BE = DF。在△ABE和△CDF中,$\begin{cases} AB = CD \\ ∠ABE = ∠CDF \\ BE = DF \end{cases}$,
∴△ABE≌△CDF(SAS)。
(2)【解】当AC = 2AB时,四边形EGCF是矩形。理由如下:
∵AC = 2OA,AC = 2AB,
∴AB = OA。
∵E是OB的中点,
∴AG⊥OB,
∴∠OEG = 90°。同理,CF⊥OD,
∴EG//CF。由
(1)得△ABE≌△CDF,
∴AE = CF。
∵EG = AE,
∴EG = CF,
∴四边形EGCF是平行四边形。
∵∠OEG = 90°,
∴四边形EGCF是矩形。
7[2024福建龙岩期中,较难]如图(1),四边形ABCD中,AD//BC,AB//CD,∠B = ∠C.
(1)求证:四边形ABCD为矩形.
(2)如图(2),M为AD的中点,在AB上取一点N,使∠BNC = 2∠DCM.
①若N为AB中点,BN = 2,求CN的长;
②若CM = 3,CN = 4,求BC的长.
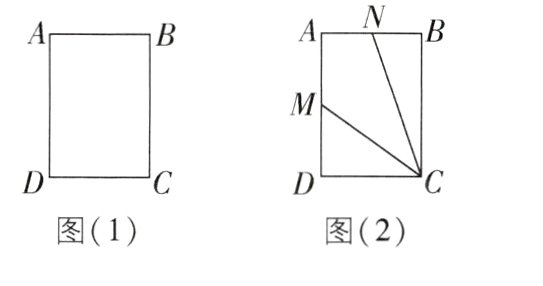
(1)求证:四边形ABCD为矩形.
(2)如图(2),M为AD的中点,在AB上取一点N,使∠BNC = 2∠DCM.
①若N为AB中点,BN = 2,求CN的长;
②若CM = 3,CN = 4,求BC的长.

答案:
(1)【证明】
∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形。
∵AB//CD,
∴∠B + ∠C = 180°。
∵∠B = ∠C,
∴∠B = ∠C = 90°,
∴四边形ABCD是矩形。
(2)【解】①如图,延长CM,BA交于点E。
∵N为AB中点,
∴AN = BN = 2,
∴AB = CD = 4。
∵AE//DC,
∴∠E = ∠MCD。
∵M为AD的中点,
∴AM = DM。
在△AEM和△DCM中,$\begin{cases} ∠E = ∠MCD \\ ∠AME = ∠CMD \\ AM = DM \end{cases}$,
∴△AME≌△DMC,
∴AE = CD = 4。
∵∠BNC = 2∠DCM = ∠NCD,
∴∠NCE = ∠ECD = ∠E,
∴CN = EN = AE + AN = 4 + 2 = 6。
②如图,由①可知,△EAM≌△CDM,EN = CN,
∴EM = CM = 3,EN = CN = 4。
设BN = x。在Rt△CBN中,$BC^{2}=CN^{2}-BN^{2}$。
在Rt△CBE中,$BC^{2}=CE^{2}-EB^{2}$,
∴$4^{2}-x^{2}=(3 + 3)^{2}-(x + 4)^{2}$,
∴$x=\frac{1}{2}$,
∴$BC=\sqrt{CN^{2}-BN^{2}}=\sqrt{4^{2}-(\frac{1}{2})^{2}}=\frac{3\sqrt{7}}{2}$。

(1)【证明】
∵AD//BC,AB//CD,
∴四边形ABCD是平行四边形。
∵AB//CD,
∴∠B + ∠C = 180°。
∵∠B = ∠C,
∴∠B = ∠C = 90°,
∴四边形ABCD是矩形。
(2)【解】①如图,延长CM,BA交于点E。
∵N为AB中点,
∴AN = BN = 2,
∴AB = CD = 4。
∵AE//DC,
∴∠E = ∠MCD。
∵M为AD的中点,
∴AM = DM。
在△AEM和△DCM中,$\begin{cases} ∠E = ∠MCD \\ ∠AME = ∠CMD \\ AM = DM \end{cases}$,
∴△AME≌△DMC,
∴AE = CD = 4。
∵∠BNC = 2∠DCM = ∠NCD,
∴∠NCE = ∠ECD = ∠E,
∴CN = EN = AE + AN = 4 + 2 = 6。
②如图,由①可知,△EAM≌△CDM,EN = CN,
∴EM = CM = 3,EN = CN = 4。
设BN = x。在Rt△CBN中,$BC^{2}=CN^{2}-BN^{2}$。
在Rt△CBE中,$BC^{2}=CE^{2}-EB^{2}$,
∴$4^{2}-x^{2}=(3 + 3)^{2}-(x + 4)^{2}$,
∴$x=\frac{1}{2}$,
∴$BC=\sqrt{CN^{2}-BN^{2}}=\sqrt{4^{2}-(\frac{1}{2})^{2}}=\frac{3\sqrt{7}}{2}$。

查看更多完整答案,请扫码查看


