《2025年初中必刷题八年级数学下册苏科版》

1 新考向跨学科综合[2024河北石家庄模拟]已知蓄电池的电压为定值,使用蓄电池时,电流I (单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图像如图所示.下列说法正确的是(　　)
　　　　　　
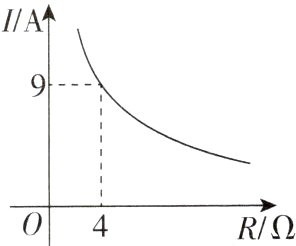
A. 函数表达式为$I=\frac{13}{R}$
B. 蓄电池的电压是18 V
C. 当$R = 6$时，$I = 4$
D. 当$I\leq10$时，$R\geq3.6$

答案： D【解析】设$I = \frac{k}{R}(R ＞ 0)$.$\because$函数图像过$(4,9)$，$\therefore k = 36$，$\therefore I = \frac{36}{R}(R ＞ 0)$，$\therefore$蓄电池的电压是$36\mathrm{V}$，$\therefore$选项A、B错误，不符合题意；当$R = 6$时，$I = \frac{36}{6} = 6$，$\therefore$选项C错误，不符合题意；当$I = 10$时，$R = 3.6$，由图像知，当$I\leq10$时，$R\geq3.6$，$\therefore$选项D正确，符合题意.

2 王老师驾驶小汽车从A地行驶到B地，行驶里程为480千米，设小汽车的行驶时间为t(单位:时)，行驶的平均速度为v(单位:千米/时)，且全程速度限定为不超过120千米/时.
　(1)求v关于t的函数表达式.
　(2)王老师上午8时驾驶小汽车从A地出发.
①王老师需要在当天13时至14时(含13时和14时)间到达B地，求小汽车行驶的平均速度v需达到的范围；
②王老师能否在当天11时30分前到达B地?说明理由.

答案： 【解】
(1)$\because vt = 480$，且全程速度限定为不超过$120$千米/时，$\therefore v$关于$t$的函数表达式为$v = \frac{480}{t}(t\geq4)$.
(2)①$8$时至$13$时的时间间隔为$5$小时，$8$时至$14$时的时间间隔为$6$小时.
将$t = 6$代入$v = \frac{480}{t}$，得$v = 80$；
将$t = 5$代入$v = \frac{480}{t}$，得$v = 96$，$\therefore$小汽车行驶的平均速度$v$需达到的范围为$80\leq v\leq96$.
②王老师不能在当天$11$时$30$分前到达B地. 理由如下：$8$时至$11$时$30$分的时间间隔为$\frac{7}{2}$小时. 将$t = \frac{7}{2}$代入$v = \frac{480}{t}$，得$v = \frac{960}{7} ＞ 120$.$\because$全程速度限定为不超过$120$千米/时，$\therefore$王老师不能在当天$11$时$30$分前到达B地.

3 [2024江苏苏州相城区质检]根据以下素材，探索完成任务.
素材1 如图，果农计划利用已有的一堵长为36 m的墙，用篱笆围成一个面积为600 m²的矩形种植基地ABCD，边AD的长不超过墙的长度.设$AB = x$ m，$AD = y$ m.
　　　　　　
素材2 现有80 m长的塑料薄膜可用于覆盖在篱笆的外围(其中薄膜宽度与篱笆高度相同，薄膜与篱笆的间隙忽略不计)
任务1 求y关于x的函数表达式
任务2 若x，y都是整数，请设计一个塑料薄膜用料最省的围建方案

答案： 【解】任务1：$\because xy = 600$，
$\therefore y = \frac{600}{x}(x\geq16\frac{2}{3})$，
故$y$关于$x$的函数表达式为$y = \frac{600}{x}(x\geq16\frac{2}{3})$.
任务2：$\because x$，$y$都是整数，$x\geq16\frac{2}{3}$且$y = \frac{600}{x}$，
$\therefore x$可以为$20,24,25,30,40,50,\cdots$.
又$\because 2x + y\leq80$，即$2x + \frac{600}{x}\leq80$，
$\therefore x$可以为$20,24,25,30$，
$\therefore$共有四种围建方案：
方案一：$AB = 20\mathrm{m}$，$BC = 30\mathrm{m}$，此时塑料薄膜用料为$70\mathrm{m}$；
易错警示：要时刻记住一个完整的函数应具备的三个要素，即自变量的取值范围、因变量的取值范围及函数表达式，因此，在根据实际情况列函数表达式或画函数图像时，一定要注意标明自变量的取值范围.
关键点拔：理解反比例函数图像的实际意义是解题关键.
方案二：$AB = 24\mathrm{m}$，$BC = 25\mathrm{m}$，此时塑料薄膜用料为$73\mathrm{m}$；
方案三：$AB = 25\mathrm{m}$，$BC = 24\mathrm{m}$，此时塑料薄膜用料为$74\mathrm{m}$；
方案四：$AB = 30\mathrm{m}$，$BC = 20\mathrm{m}$，此时塑料薄膜用料为$80\mathrm{m}$.
故塑料薄膜用料最省的围建方案为$AB = 20\mathrm{m}$，$BC = 30\mathrm{m}$.

4 [2024浙江台州一模]一辆出租车从甲地到乙地，当平均速度为v(km/h)时，所用时间为t(h)，则t关于v的函数图像大致是(　　)
　

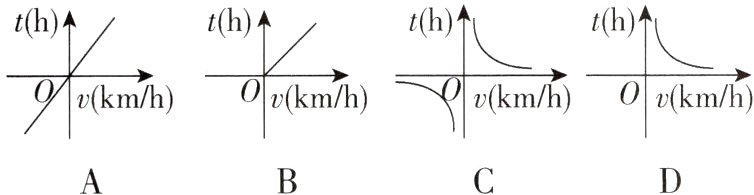
答案： D【解析】设甲、乙两地之间的距离为$s\mathrm{km}$，则$vt = s$(定值)，$\therefore t = \frac{s}{v}(v ＞ 0,t ＞ 0)$，符合反比例函数的一般形式，且速度和时间均为正数，图像应为在第一象限的双曲线.

5 某学校要种植一块面积为200 m²的长方形草坪，要求两边长均不小于10 m，则草坪的一边长y(单位:m)随另一边长x(单位:m)的变化而变化的图像可能是(　　)

答案： C【解析】$\because$草坪面积为$200\mathrm{m}^2$，$\therefore xy = 200$，则$y$与$x$之间的函数关系式为$y = \frac{200}{x}$.$\because$两边长均不小于$10\mathrm{m}$，$\therefore x\geq10$，$y\geq10$，则$10\leq x\leq20$，故选C.