第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
1[中]如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD交于点O. 关于四边形ABCD的形状,甲、乙、丙三人的说法如下:甲:若添加“AB//CD”,则四边形ABCD是菱形;乙:若添加“∠BAD=90°”,则四边形ABCD是矩形;丙:若添加“∠ABC=∠BCD=90°”,则四边形ABCD是正方形. 其中说法正确的是 ( )
A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙

A. 甲、乙 B. 甲、丙
C. 乙、丙 D. 甲、乙、丙

答案:
B【解析】
∵AB = AD,BC = DC,
∴AC垂直平分BD.若添加“AB//CD”,则∠ABD = ∠BDC.
∵BC = DC,
∴∠BDC = ∠DBC,
∴∠ABO = ∠CBO.又
∵BO = BO,∠BOA = ∠BOC,
∴△ABO≌△CBO(ASA),
∴BA = BC,
∴AB = BC = CD = DA,
∴四边形ABCD是菱形,故甲说法正确.若添加“∠BAD = 90°”,无法证明四边形ABCD是矩形,故乙说法错误;若添加“∠ABC = ∠BCD = 90°”,则∠ABC + ∠BCD = 180°,
∴AB//CD,由证选项A可知四边形ABCD是菱形.
∵∠ABC = 90°,
∴四边形ABCD是正方形,故丙说法正确.故选B.
∵AB = AD,BC = DC,
∴AC垂直平分BD.若添加“AB//CD”,则∠ABD = ∠BDC.
∵BC = DC,
∴∠BDC = ∠DBC,
∴∠ABO = ∠CBO.又
∵BO = BO,∠BOA = ∠BOC,
∴△ABO≌△CBO(ASA),
∴BA = BC,
∴AB = BC = CD = DA,
∴四边形ABCD是菱形,故甲说法正确.若添加“∠BAD = 90°”,无法证明四边形ABCD是矩形,故乙说法错误;若添加“∠ABC = ∠BCD = 90°”,则∠ABC + ∠BCD = 180°,
∴AB//CD,由证选项A可知四边形ABCD是菱形.
∵∠ABC = 90°,
∴四边形ABCD是正方形,故丙说法正确.故选B.
2[2023四川成都调研,中]如图,在边长为12的正方形ABCD中,点P在AD上,且不与A,D重合,点H在AB上,且不与A,B重合,连接BP,CH,BP与CH交于点E. 若BP=CH,AP=5,则线段BE的长是 ( )
A. 4 B. $\frac{30}{13}$ C. $\frac{60}{13}$ D. 5
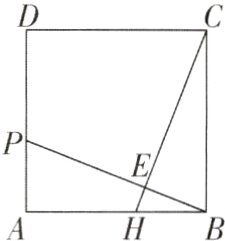
A. 4 B. $\frac{30}{13}$ C. $\frac{60}{13}$ D. 5

答案:
C【解析】
∵四边形ABCD是正方形,
∴AB = BC,∠A = ∠ABC = 90°.在Rt△PAB和Rt△HBC中,$\begin{cases}BP = HC,\\AB = BC,\end{cases} $
∴Rt△PAB≌Rt△HBC(HL),
∴BH = AP = 5,∠PBA = ∠BCH.
∵正方形ABCD的边长为12,
∴AB = BC = 12.在Rt△HBC中,由勾股定理,得$CH = \sqrt{BH² + BC²}=\sqrt{5² + 12²}=13.$
∵∠PBA = ∠BCH,∠BCH + ∠BHC = 90°,
∴∠PBA + ∠BHC = 90°,
∴∠BEH = 90°,
∴BP⊥CH,
∴$S_{△HBC}=\frac{1}{2}CH·BE=\frac{1}{2}HB·BC,$
∴$\frac{1}{2}×13×BE=\frac{1}{2}×5×12,$解得$BE = \frac{60}{13},$即线段BE的长为$\frac{60}{13}.$故选C.
∵四边形ABCD是正方形,
∴AB = BC,∠A = ∠ABC = 90°.在Rt△PAB和Rt△HBC中,$\begin{cases}BP = HC,\\AB = BC,\end{cases} $
∴Rt△PAB≌Rt△HBC(HL),
∴BH = AP = 5,∠PBA = ∠BCH.
∵正方形ABCD的边长为12,
∴AB = BC = 12.在Rt△HBC中,由勾股定理,得$CH = \sqrt{BH² + BC²}=\sqrt{5² + 12²}=13.$
∵∠PBA = ∠BCH,∠BCH + ∠BHC = 90°,
∴∠PBA + ∠BHC = 90°,
∴∠BEH = 90°,
∴BP⊥CH,
∴$S_{△HBC}=\frac{1}{2}CH·BE=\frac{1}{2}HB·BC,$
∴$\frac{1}{2}×13×BE=\frac{1}{2}×5×12,$解得$BE = \frac{60}{13},$即线段BE的长为$\frac{60}{13}.$故选C.
3[中]如图,在正方形ABCD中,AB=4,点P在对角线BD上,PE⊥BC,PF⊥CD,垂足分别为E,F,连接AP,EF,以下结论:①AP=EF;②AP⊥EF;③EF的最小值为2. 其中结论正确的是________. (填序号)
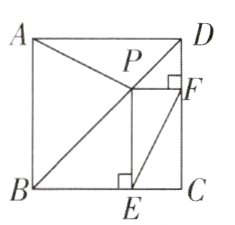

答案:
①②【解析】连接PC,如图
(1).
∵四边形ABCD是正方形,
∴∠BCD = 90°,AD = CD,∠ADP = ∠CDP.
∵PE⊥BC,PF⊥CD,
∴四边形PECF为矩形,
∴PC = EF.在△ADP和△CDP中,$\begin{cases}AD = CD,\\∠ADP = ∠CDP,\\DP = DP,\end{cases} $
∴△ADP≌△CDP(SAS),
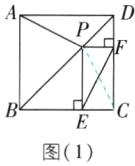
∴AP = PC,
∴AP = EF,故①正确.
延长FP与AB交于点M,延长AP与EF交于点H,如图
(2).易知PM⊥AB,
∵BD平分∠ABC,PE⊥BC,
∴PM = PE.
∵AP = EF,∠AMP = ∠EPF = 90°,
∴Rt△AMP≌Rt△FPE(HL),
∴∠BAP = ∠PFE.
∵∠AMP = 90°,
∴∠BAP + ∠APM = 90°.
∵∠APM = ∠HPF,
∴∠PFH + ∠HPF = 90°,
∴∠PHF = 90°,
∴AP⊥EF,故②正确.
∵EF = AP,
∴当AP的值最小时,EF的值最小,则当AP⊥BD,即$AP = \frac{1}{2}BD$时,EF的值最小.
∵AB = 4,
∴$BD = 4\sqrt{2},$
∴$AP = 2\sqrt{2},$
∴EF的最小值为$2\sqrt{2},$故③不正确.综上,结论正确的是①②.故答案为①②.
①②【解析】连接PC,如图
(1).
∵四边形ABCD是正方形,
∴∠BCD = 90°,AD = CD,∠ADP = ∠CDP.
∵PE⊥BC,PF⊥CD,
∴四边形PECF为矩形,
∴PC = EF.在△ADP和△CDP中,$\begin{cases}AD = CD,\\∠ADP = ∠CDP,\\DP = DP,\end{cases} $
∴△ADP≌△CDP(SAS),

∴AP = PC,
∴AP = EF,故①正确.
延长FP与AB交于点M,延长AP与EF交于点H,如图
(2).易知PM⊥AB,
∵BD平分∠ABC,PE⊥BC,
∴PM = PE.
∵AP = EF,∠AMP = ∠EPF = 90°,
∴Rt△AMP≌Rt△FPE(HL),
∴∠BAP = ∠PFE.
∵∠AMP = 90°,
∴∠BAP + ∠APM = 90°.
∵∠APM = ∠HPF,
∴∠PFH + ∠HPF = 90°,
∴∠PHF = 90°,
∴AP⊥EF,故②正确.
∵EF = AP,
∴当AP的值最小时,EF的值最小,则当AP⊥BD,即$AP = \frac{1}{2}BD$时,EF的值最小.
∵AB = 4,
∴$BD = 4\sqrt{2},$
∴$AP = 2\sqrt{2},$
∴EF的最小值为$2\sqrt{2},$故③不正确.综上,结论正确的是①②.故答案为①②.
4[2023江苏苏州姑苏区期中,中]如图,四边形ABCD是边长为8的正方形,点E在边CD上,DE=2. 作EF//BC,分别交AC,AB于点G,F,M,N分别是AG,BE的中点,则MN的长为_______.



答案:
5【解析】如图,连接FM,FC.
∵四边形ABCD是正方形,EF//BC,
∴∠BAC = 45°,
∴△AFG为等腰直角三角形.
∵M是AG的中点,
∴FM⊥AG,
∴△FMC是直角三角形.
∵N是BE的中点,易得四边形BCEF是矩形,
∴点N在CF上,且是CF的中点,
∴$MN = \frac{1}{2}FC.$
∵DE = 2,BC = DC = 8,
∴CE = 6,
∴$FC = BE = \sqrt{BC² + CE²}=10,$
∴$MN = \frac{1}{2}FC = 5.$
5【解析】如图,连接FM,FC.
∵四边形ABCD是正方形,EF//BC,
∴∠BAC = 45°,
∴△AFG为等腰直角三角形.
∵M是AG的中点,
∴FM⊥AG,
∴△FMC是直角三角形.
∵N是BE的中点,易得四边形BCEF是矩形,
∴点N在CF上,且是CF的中点,
∴$MN = \frac{1}{2}FC.$
∵DE = 2,BC = DC = 8,
∴CE = 6,
∴$FC = BE = \sqrt{BC² + CE²}=10,$
∴$MN = \frac{1}{2}FC = 5.$

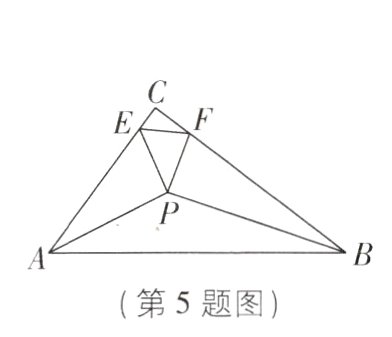
5[2024江苏盐城质检,较难]如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,AB=10,两锐角的角平分线交于点P,点E,F分别在边AC,BC上,且∠EPF=45°,连接EF,则△CEF的周长为________.
答案:
4【解析】如图,过点P作PM⊥AC于M,PN⊥BC于N,PK⊥AB于K,则∠C = ∠PMC = ∠PNC = 90°.在EA上取一点J,使得MJ = FN,连接PJ.
∵BP平分∠ABC,AP平分∠CAB,
∴PM = PK = PN,
∴四边形PMCN是正方形,
∴CM = CN = PM,∠MPN = 90°.在△PMJ和△PNF中,$\begin{cases}PM = PN,\\∠PMJ = ∠PNF = 90°,\\MJ = NF,\end{cases}$
∴△PMJ≌△PNF(SAS),
∴∠MPJ = ∠FPN,PJ = PF,
∴∠JPF = ∠MPN = 90°.
∵∠EPF = 45°,
∴∠EPF = ∠EPJ = 45°.在△PEF和△PEJ中,$\begin{cases}PE = PE,\\∠EPF = ∠EPJ,\\PF = PJ,\end{cases} $
∴△PEF≌△PEJ(SAS),
∴EF = EJ = EM + MJ = EM + FN,
∴△CEF的周长为CE + EF + CF = CE + EM + CF + FN = CM + CN = 2PM.
∵$S_{△ABC}=\frac{1}{2}BC·AC=\frac{1}{2}(AC + BC + AB)·PM,$
∴24 = 12PM,
∴PM = 2,
∴△ECF的周长为4.

4【解析】如图,过点P作PM⊥AC于M,PN⊥BC于N,PK⊥AB于K,则∠C = ∠PMC = ∠PNC = 90°.在EA上取一点J,使得MJ = FN,连接PJ.
∵BP平分∠ABC,AP平分∠CAB,
∴PM = PK = PN,
∴四边形PMCN是正方形,
∴CM = CN = PM,∠MPN = 90°.在△PMJ和△PNF中,$\begin{cases}PM = PN,\\∠PMJ = ∠PNF = 90°,\\MJ = NF,\end{cases}$
∴△PMJ≌△PNF(SAS),
∴∠MPJ = ∠FPN,PJ = PF,
∴∠JPF = ∠MPN = 90°.
∵∠EPF = 45°,
∴∠EPF = ∠EPJ = 45°.在△PEF和△PEJ中,$\begin{cases}PE = PE,\\∠EPF = ∠EPJ,\\PF = PJ,\end{cases} $
∴△PEF≌△PEJ(SAS),
∴EF = EJ = EM + MJ = EM + FN,
∴△CEF的周长为CE + EF + CF = CE + EM + CF + FN = CM + CN = 2PM.
∵$S_{△ABC}=\frac{1}{2}BC·AC=\frac{1}{2}(AC + BC + AB)·PM,$
∴24 = 12PM,
∴PM = 2,
∴△ECF的周长为4.

6[2024江苏苏州期末,中]如图,已知四边形ABCD和四边形CEFG都是正方形,在BC上截取BM,延长CD到点N,使BM=DN=CE,求证:四边形AMFN是正方形.


答案:
【证明】
∵四边形ABCD和四边形CEFG都是正方形,
∴AB = BC = CD = AD,∠B = ∠ADC = ∠E = ∠CGF = 90°,CE = EF = FG = CG,
∴∠FGN = ∠ADN = 90°.
∵BM = DN = CE,
∴BM = DN = EF = FG = CG,
∴BC = BM + CM = CE + CM = EM,CD = CG + DG = DN + DG = NG.
在△ABM,△MEF,△NGF,△ADN中,AB = ME = NG = AD,∠B = ∠E = ∠NGF = ∠ADN = 90°,BM = EF = GF = DN,
∴△ABM≌△MEF≌△NGF≌△ADN(SAS),
∴AM = MF = NF = AN,∠BAM = ∠DAN,
∴四边形AMFN是菱形.
∵∠BAD = ∠BAM + ∠DAM = 90°,
∴∠DAN + ∠DAM = 90° = ∠MAN,
∴四边形AMFN是正方形.
∵四边形ABCD和四边形CEFG都是正方形,
∴AB = BC = CD = AD,∠B = ∠ADC = ∠E = ∠CGF = 90°,CE = EF = FG = CG,
∴∠FGN = ∠ADN = 90°.
∵BM = DN = CE,
∴BM = DN = EF = FG = CG,
∴BC = BM + CM = CE + CM = EM,CD = CG + DG = DN + DG = NG.
在△ABM,△MEF,△NGF,△ADN中,AB = ME = NG = AD,∠B = ∠E = ∠NGF = ∠ADN = 90°,BM = EF = GF = DN,
∴△ABM≌△MEF≌△NGF≌△ADN(SAS),
∴AM = MF = NF = AN,∠BAM = ∠DAN,
∴四边形AMFN是菱形.
∵∠BAD = ∠BAM + ∠DAM = 90°,
∴∠DAN + ∠DAM = 90° = ∠MAN,
∴四边形AMFN是正方形.
7核心素养·推理能力[难]在Rt△AEB中,∠AEB=90°,以斜边AB为边向上作正方形ABCD,若正方形ABCD的对角线交于点O(如图(1)).
(1)求证:EO平分∠AEB.
(2)试猜想线段OE与EB,EA之间的数量关系,并证明你的结论.
(3)如图(2),过点C作CF⊥EB交EB延长线于F,过点D作GH//EF,分别交EA延长线和FC延长线于H,G. 求证:四边形EFGH为正方形.

(1)求证:EO平分∠AEB.
(2)试猜想线段OE与EB,EA之间的数量关系,并证明你的结论.
(3)如图(2),过点C作CF⊥EB交EB延长线于F,过点D作GH//EF,分别交EA延长线和FC延长线于H,G. 求证:四边形EFGH为正方形.

答案:
(1)【证明】如图,延长EA至点F,使AF = BE,连接OF.
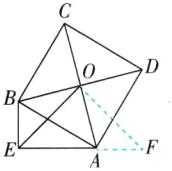
∵四边形ABCD是正方形,
∴∠ABC = ∠BAD = 90°,AC⊥BD,∠ABO = ∠BAO = 45°,OB = OA,
∴∠AOB = 90°,
∴∠AEB + ∠AOB = 90° + 90° = 180°,
∴∠OBE + ∠OAE = 180°.
又
∵∠OAE + ∠OAF = 180°,
∴∠OBE = ∠OAF,
∴△OBE≌△OAF(SAS),
∴OE = OF,∠BOE = ∠AOF.
∵∠BOE + ∠AOE = 90°,
∴∠AOF + ∠AOE = 90°,
∴∠EOF = 90°,
∴△EOF是等腰直角三角形,
∴∠OEF = ∠OFE = 45°,
∴∠OEB = ∠OEA = 45°,即EO平分∠AEB.
(2)【解$】EA + EB = \sqrt{2}OE.$证明如下:由
(1)知BE = AF,△EOF是等腰直角三角形,
∴2OE² = EF²,即2OE² = (EA + EB)²,
∴$EA + EB = \sqrt{2}OE.(3)【$证明】
∵四边形ABCD是正方形,
∴∠BAD = 90°,AB = AD.
∵GH//EF,
∴∠BEA + ∠H = 180°,
∴∠BEA = ∠H = ∠BAD = 90°,
∴∠EAB + ∠DAH = 90°,∠EAB + ∠ABE = 90°,
∴∠ABE = ∠DAH.
在△ABE与△DAH中,$\begin{cases}∠BEA = ∠H,\\∠ABE = ∠DAH,\\AB = DA,\end{cases}$
∴△ABE≌△DAH(AAS).
同理可得△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,
∴CG = BF = AE = DH,DG = CF = BE = AH,
∴CG + FC = BF + BE = AE + AH = DH + DG,即FG = EF = EH = GH.
又
∵∠H = 90°,
∴四边形EFGH为正方形.
(1)【证明】如图,延长EA至点F,使AF = BE,连接OF.

∵四边形ABCD是正方形,
∴∠ABC = ∠BAD = 90°,AC⊥BD,∠ABO = ∠BAO = 45°,OB = OA,
∴∠AOB = 90°,
∴∠AEB + ∠AOB = 90° + 90° = 180°,
∴∠OBE + ∠OAE = 180°.
又
∵∠OAE + ∠OAF = 180°,
∴∠OBE = ∠OAF,
∴△OBE≌△OAF(SAS),
∴OE = OF,∠BOE = ∠AOF.
∵∠BOE + ∠AOE = 90°,
∴∠AOF + ∠AOE = 90°,
∴∠EOF = 90°,
∴△EOF是等腰直角三角形,
∴∠OEF = ∠OFE = 45°,
∴∠OEB = ∠OEA = 45°,即EO平分∠AEB.
(2)【解$】EA + EB = \sqrt{2}OE.$证明如下:由
(1)知BE = AF,△EOF是等腰直角三角形,
∴2OE² = EF²,即2OE² = (EA + EB)²,
∴$EA + EB = \sqrt{2}OE.(3)【$证明】
∵四边形ABCD是正方形,
∴∠BAD = 90°,AB = AD.
∵GH//EF,
∴∠BEA + ∠H = 180°,
∴∠BEA = ∠H = ∠BAD = 90°,
∴∠EAB + ∠DAH = 90°,∠EAB + ∠ABE = 90°,
∴∠ABE = ∠DAH.
在△ABE与△DAH中,$\begin{cases}∠BEA = ∠H,\\∠ABE = ∠DAH,\\AB = DA,\end{cases}$
∴△ABE≌△DAH(AAS).
同理可得△ABE≌△BCF,△ADH≌△DCG,△DCG≌△CBF,
∴CG = BF = AE = DH,DG = CF = BE = AH,
∴CG + FC = BF + BE = AE + AH = DH + DG,即FG = EF = EH = GH.
又
∵∠H = 90°,
∴四边形EFGH为正方形.
查看更多完整答案,请扫码查看


