《2025年初中必刷题八年级数学下册苏科版》

1[2024广东中山一模]下列函数中,y是x的反比例函数的是　　　　　　　　　　　(　　　)
A. $y=-x$
B. $y=-\frac{2}{x}$
C. $y=1-\frac{1}{x}$
D. $y=x^{2}-2x+1$

答案： 1.B　[解析]A选项,y = -x,不符合反比例函数的定义，故此选项错误;B选项，y = -$\frac{2}{x}$,符合反比例函数的定义，故此选项正确;C选项，y = 1 - $\frac{1}{x}$，不符合反比例函数的定义，故此选项错误;D选项,y = x² - 2x + 1,不符合反比例函数的定义，故此选项错误.故选B.

2[2024浙江杭州江干区期末]已知x与y成反比例,z与x成正比例,则y是z的　　　(　　　)
A. 正比例函数
B. 反比例函数
C. 一次函数
D. 不能确定

答案： 2.B　[解析]
∵x与y成反比例,z与x成正比例,
∴设x = $\frac{k}{y}$(k为常数,k≠0),z = ax(a为常数，a≠0),
∴x = $\frac{z}{a}$,则$\frac{k}{y}$ = $\frac{z}{a}$,故yz = ka,
∴y = $\frac{ka}{z}$,则y是z的反比例函数,故选B.

3[2023浙江温州期中]已知反比例函数$y=-\frac{3}{2x}$.
(1)写出这个函数中k的值;
(2)求当$x=-10$时,函数y的值;
(3)求当$y=6$时,自变量x的值.

答案： 3.[解]
(1)y = -$\frac{3}{2x}$ = $\frac{-\frac{3}{2}}{x}$,故k = -$\frac{3}{2}$.
(2)当x = -10时,y = -$\frac{3}{2\times(-10)}$ = $\frac{3}{20}$.
(3)当y = 6时,-$\frac{3}{2x}$ = 6,解得x = -$\frac{1}{4}$.
经检验,x = -$\frac{1}{4}$是原方程的解.

4[2023上海青浦区期末]下列各种关系中,成反比例关系的是　　　　　　　　　　　(　　　)
A. 圆的面积S与半径r
B. 速度v一定,行驶路程s与时间t
C. 平行四边形面积S一定,它的底a和高h
D. 一个人的跑步速度与他的体重

答案： 4.C　[解析]A圆的面积S = πr²,S与r不成反比例关系，故A错误；B速度v一定时，行驶路程s和时间t的关系为s = vt，不成反比例关系，故B错误；C平行四边形面积S一定，它的底a和高h的关系为a = $\frac{S}{h}$，成反比例关系，故C正确；D一个人的跑步速度与他的体重，不成反比例关系，故D错误.

5[2023江苏宿迁调研]已知$\frac{1}{x^{2}}$和y成正比例,$\frac{1}{y}$与z成反比例,那么$x^{2}$和z　　　　　　(　　　)
A. 成正比例
B. 成反比例
C. 既不成正比例,也不成反比例
D. 既成正比例,也成反比例

答案： 5.B　[解析]因为$\frac{1}{x²}$和y成正比例,所以y = k₁$\frac{1}{x²}$.又因为$\frac{1}{y}$与z成反比例,所以z = $\frac{k₂}{\frac{1}{y}}$,所以z = k₂y = k₂k₁$\frac{1}{x²}$,即z与x²成反比例.故选B.

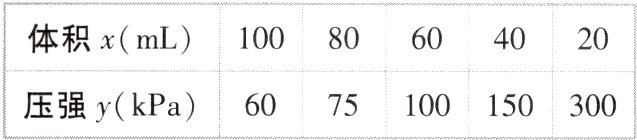
6[2024山东临沂质检]在温度不变的条件下,某气体的压强和气体体积对应数值如下表,则可以反映y与x之间的关系的式子是　　(　　　)

A. $y = 6000x$
B. $y = 3000x$
C. $y=\frac{6000}{x}$
D. $y=\frac{3000}{x}$

答案： 6.C　[解析]由表格知,xy = 6000,即y = $\frac{6000}{x}$,故选C.

7[2023江苏南京秦淮区期末]小明要把一篇27000字的调查报告录入电脑,则其录入的时间t(分)与录入文字的平均速度v(字/分)之间的函数表达式应为$t =$_______$(v＞0)$.

答案： 7.$\frac{27000}{v}$　[解析]由录入的时间 = 录入总量÷录入速度，可得t = $\frac{27000}{v}$(v＞0).

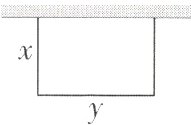
8如图,某养鸡场利用一面长为11m的墙和一段栅栏围了一个矩形空地,面积为60m²,设与墙垂直的边的长度为xm,与墙平行的边的长度为ym.
(1)直接写出y与x的函数关系式;
(2)现有两种方案:$x = 5$或$x = 6$,试选择合理的设计方案,并求此栅栏的总长.

答案： 8.[解]
(1)y = $\frac{60}{x}$.依题意得xy = 60,
∴y与x的函数关系式为y = $\frac{60}{x}$.
(2)当x = 5时,y = $\frac{60}{5}$ = 12.
∵12＞11,
∴不符合题意，舍去.
当x = 6时,y = $\frac{60}{6}$ = 10.
∵10＜11,
∴符合题意，此栅栏的总长为2x + y = 2×6 + 10 = 22.
故应选择x = 6的设计方案，此栅栏的总长为22m.

9若函数$y=(m + 1)x^{m^{2}-2}$是y关于x的反比例函数，则$m =$_______.

答案： 9.1　[解析]
∵函数$y = (m + 1)x^(m² - 2)$是y关于x的反比例函数,
∴m + 1≠0,m² - 2 = -1,
∴m = 1,故答案为1.