《2025年初中必刷题八年级数学下册苏科版》

1[2024河北沧州校级一模，中]已知△ABC（如图（1）），按图（2）、图（3）所示的尺规作图痕迹，（不需借助三角形全等）就能推出四边形ABCD是平行四边形的依据是（　　）

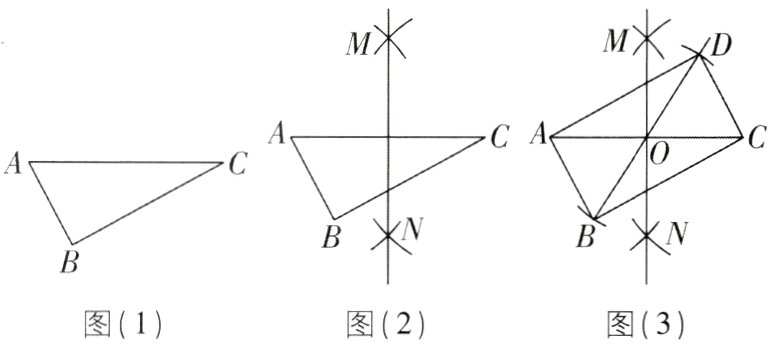
A. 两组对边分别平行的四边形是平行四边形
B. 一组对边平行且相等的四边形是平行四边形
C. 对角线互相平分的四边形是平行四边形
D. 两组对边分别相等的四边形是平行四边形

答案： C　[解析]由作图可知MN垂直平分线段AC,OB=OD,
∴OA=OC,
∴四边形ABCD是平行四边形(对角线互相平分的四边形是平行四边形).故选C.

2[2023北京海淀区期中，中]如图，▱ABCD的对角线交于点O，点M，N，P，Q分别是▱ABCD四条边上不重合的点. 下列条件：①AQ=CN，AM=CP；②MP，NQ均经过点O；③NQ经过点O，AQ=CN. 其中，能判定四边形MNPQ是平行四边形的有_______（填序号）.

答案：
①②　[解析]
∵四边形ABCD是平行四边形，
∴AB = CD，AD = BC，∠BAD = ∠BCD，∠ABC = ∠CDA.
∵AQ = CN，AM = CP，
∴DQ = BN，BM = DP，①△AMQ≌△CPN（SAS），
∴△BMN≌△DPQ（SAS），
∴MQ = NP，MN = PQ，则四边形MNPQ是平行四边形，故①符合题意；②
∵□ABCD的对角线交于点O，MP，NQ均经过点O，
∴OQ = ON，OP = OM，则四边形MNPQ是平行四边形，故②符合题意；③NQ经过点O，AQ = CN，M，P的位置未知，
∴不能判定四边形MNPQ是平行四边形，故③不符合题意；

3[2022山东临沂中考，中]如图，在正六边形ABCDEF中，M，N是对角线BE上的两点. 添加下列条件中的一个：①BM=EN；②∠FAN=∠CDM；③AM=DN；④∠AMB=∠DNE，能使四边形AMDN是平行四边形的是_______（填上所有符合要求的条件的序号）.

答案：
①②④　[解析]如图,连接AD,交BE于点O. 在正六边形ABCDEF中，∠OAF = ∠ODC，∠ABM = ∠DEN，AB = DE，OA = OD，OB = OE. ①
∵BM = EN，OB = OE，
∴OM = ON. 又
∵OA = OD，
∴四边形AMDN是平行四边形，故①符合题意. ②
∵∠FAN = ∠CDM，∠CDA = ∠DAF，
∴∠OAN = ∠ODM，
∴AN//DM. 又
∵OA = OD，∠AON = ∠DOM，
∴△AON≌△DOM（ASA），
∴AN = DM，
∴四边形AMDN是平行四边形，故②符合题意. ③无法得出四边形AMDN是平行四边形，故③不符合题意. ④
∵∠AMB = ∠DNE，∠ABM = ∠DEN，AB = DE，
∴△ABM≌△DEN（AAS），
∴AM = DN.
∵∠AMB + ∠AMN = 180°，∠DNM + ∠DNE = 180°，
∴∠AMN = ∠DNM，
∴AM//DN，
∴四边形AMDN是平行四边形，故④符合题意. 故答案为①②④.

4[2024山东青岛期末，中]如图，P是△ABC的边AB的中点，连接CP，作BE⊥CP于E，AD⊥CP交CP的延长线于点D，连接AE，BD.
（1）求证：四边形ADBE是平行四边形；
（2）若BE平分∠DBC，求△ABC与四边形ADBE的面积之比.

答案：
(1)[证明]
∵P为AB中点，
∴AP = BP.
∵BE⊥CP,AD⊥CP,
∴∠ADP = ∠BEP = 90°.在△ADP和△BEP中，$\begin{cases} \angle ADP=\angle BEP \\ \angle APD=\angle BPE \\ AP = BP \end{cases}$，
∴△ADP≌△BEP(AAS),
∴DP = EP.
∵AP = BP,
∴四边形ADBE是平行四边形.
(2)[解]
∵BE⊥CP,
∴∠BED = ∠BEC = 90°.
∵BE平分∠DBC,
∴∠DBE = ∠CBE.在△BED和△BEC中，$\begin{cases} \angle BED=\angle BEC \\ BE = BE \\ \angle DBE=\angle CBE \end{cases}$，
∴△BED≌△BEC(ASA),
∴CE = DE.由
(1)得DP = EP,
∴CP=$\frac{3}{2}$DE.由
(1)可知，四边形ADBE是平行四边形，
∴S四边形ADBE = 2S△ADE.
∵AP = BP,
∴S△ABC = 2S△ACP.
∵$\frac{S_{\triangle ACP}}{S_{\triangle ADE}}=\frac{\frac{1}{2}CP\cdot AD}{\frac{1}{2}DE\cdot AD}=\frac{CP}{DE}=\frac{3}{2}$，
∴$\frac{S_{\triangle ABC}}{S_{四边形ADBE}}=\frac{2S_{\triangle ACP}}{2S_{\triangle ADE}}=\frac{S_{\triangle ACP}}{S_{\triangle ADE}}=\frac{3}{2}$.

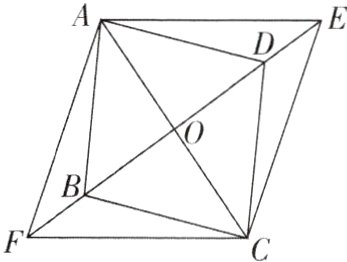
5[2023江苏宿迁质检，中]如图，在平行四边形ABCD中，对角线BD，AC相交于点O，点E，F分别在BD，DB的延长线上，且DE=BF，连接AE，AF，CF，CE.
（1）求证：四边形AFCE为平行四边形；
（2）若AC平分∠EAF，∠AEC=60°，OA=4，求四边形AFCE的周长；
（3）若DE=$\frac{1}{3}$OD，BF=$\frac{1}{3}$OB，四边形AFCE是平行四边形吗？若DE=$\frac{1}{n}$OD，BF=$\frac{1}{n}$OB，四边形AFCE是平行四边形吗？简单说明理由.

答案：
(1)[证明]
∵四边形ABCD为平行四边形，
∴OD = OB，OA = OC.
∵DE = BF，
∴OD + DE = OB + BF，
∴OE = OF. 又
∵OA = OC，
∴四边形AFCE为平行四边形.
(2)[解]
∵AC平分∠EAF，
∴∠EAC = ∠FAC.
∵四边形AFCE为平行四边形，OA = 4，
∴CE//AF，OC = OA = 4，
∴∠ECA = ∠FAC，AC = 4 + 4 = 8，
∴∠EAC = ∠ECA，
∴AE = CE，
∴AE = CE = FC = AF.
∵∠AEC = 60°，
∴△EAC是等边三角形，
∴AE = AC = 8，
∴AF + CF + CE + AE = 4AE = 32，
∴四边形AFCE的周长是32.
(3)[解]若DE=$\frac{1}{3}$OD，BF=$\frac{1}{3}$OB，四边形AFCE是平行四边形. 理由：
∵DE=$\frac{1}{3}$OD，BF=$\frac{1}{3}$OB，OD = OB，
∴DE = BF，
∴OB + BF = OD + DE，即OF = OE. 又
∵OA = OC，
∴四边形AFCE为平行四边形.若DE=$\frac{1}{n}$OD，BF=$\frac{1}{n}$OB，四边形AFCE是平行四边形. 理由：
∵DE=$\frac{1}{n}$OD，BF=$\frac{1}{n}$OB，OD = OB，
∴DE = BF，
∴OB + BF = OD + DE，即OF = OE.
∵OA = OC，
∴四边形AFCE是平行四边形.