第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
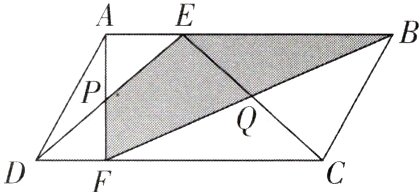
1[2023山东济南模拟,中]如图,F是▱ABCD的边CD上的点,Q是BF的中点,连接CQ并延长交AB于点E,连接AF与DE相交于点P.若$S_{\triangle APD}=2\ cm^{2},S_{\triangle BQE}=8\ cm^{2}$,则阴影部分的面积为( )
A. 24 cm²
B. 17 cm²
C. 18 cm²
D. 10 cm²

A. 24 cm²
B. 17 cm²
C. 18 cm²
D. 10 cm²
答案:
C【解析】如图,
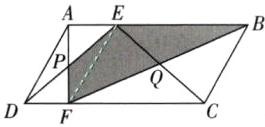
连接EF.
∵F是□ABCD的边CD上的点,
∴BE//CF,
∴∠EBF = ∠CFB,∠BEC = ∠FCE.
∵BQ = FQ,
∴△EBQ≌△CFQ(AAS),
∴BE = CF,EQ = CQ,
∴四边形EBCF是平行四边形,
∴$S_{△BEF}=2S_{△BQC}=16 cm². $易得四边形ADFE是平行四边形,
∴$S_{△APD}=S_{△EPF}=2 cm²,$
∴$S_{阴影}=S_{△EPF}+S_{△EBF}=18 cm². $故选C.
C【解析】如图,

连接EF.
∵F是□ABCD的边CD上的点,
∴BE//CF,
∴∠EBF = ∠CFB,∠BEC = ∠FCE.
∵BQ = FQ,
∴△EBQ≌△CFQ(AAS),
∴BE = CF,EQ = CQ,
∴四边形EBCF是平行四边形,
∴$S_{△BEF}=2S_{△BQC}=16 cm². $易得四边形ADFE是平行四边形,
∴$S_{△APD}=S_{△EPF}=2 cm²,$
∴$S_{阴影}=S_{△EPF}+S_{△EBF}=18 cm². $故选C.
2[2024江苏徐州期末,较难]如图,AB = CD = 2,∠A = 15°,∠C = 15°,∠D = 105°,则线段AD的长为_______.


答案:
$\sqrt{2}$【解析】过点A作AE//CD,且AE = CD,连接BE,CE,如图.
∵AE//CD,AE = CD,
∴四边形ADCE是平行四边形,
∴AD = CE,AD//CE.
∵AE//CD,AD//CE,∠D = 105°,
∴∠DAE = 180° - 105° = 75°,∠DCE = 180° - 105° = 75°. 又
∵∠DAB = 15°,∠DCB = 15°,
∴∠BAE = ∠DAE - ∠DAB = 75° - 15° = 60°,∠BCE = ∠DCE + ∠DCB = 75° + 15° = 90°.
∵∠BAE = 60°,AE = CD = AB,
∴△ABE是等边三角形,
∴BE = AB = 2,∠ABE = 60°.
∵∠DAB = ∠DCB,∠DOA = ∠COB,∠D = 105°,
∴∠D = ∠ABC = 105°,
∴∠EBC = ∠ABC - ∠ABE = 105° - 60° = 45°,
∴∠EBC = ∠BEC = 45°,
∴BC = EC. 在Rt△BCE中,EC² + BC² = BE²,即2BC² = BE²,
∴2BC² = 4,解得BC = $\sqrt{2}$(负值已舍去),即AD = CE = BC = $\sqrt{2}$. 故答案为$\sqrt{2}$.

$\sqrt{2}$【解析】过点A作AE//CD,且AE = CD,连接BE,CE,如图.
∵AE//CD,AE = CD,
∴四边形ADCE是平行四边形,
∴AD = CE,AD//CE.
∵AE//CD,AD//CE,∠D = 105°,
∴∠DAE = 180° - 105° = 75°,∠DCE = 180° - 105° = 75°. 又
∵∠DAB = 15°,∠DCB = 15°,
∴∠BAE = ∠DAE - ∠DAB = 75° - 15° = 60°,∠BCE = ∠DCE + ∠DCB = 75° + 15° = 90°.
∵∠BAE = 60°,AE = CD = AB,
∴△ABE是等边三角形,
∴BE = AB = 2,∠ABE = 60°.
∵∠DAB = ∠DCB,∠DOA = ∠COB,∠D = 105°,
∴∠D = ∠ABC = 105°,
∴∠EBC = ∠ABC - ∠ABE = 105° - 60° = 45°,
∴∠EBC = ∠BEC = 45°,
∴BC = EC. 在Rt△BCE中,EC² + BC² = BE²,即2BC² = BE²,
∴2BC² = 4,解得BC = $\sqrt{2}$(负值已舍去),即AD = CE = BC = $\sqrt{2}$. 故答案为$\sqrt{2}$.

3[2023浙江温州鹿城区期中,中]如图(1),在▱ABCD中,∠BAD的平分线恰好经过边CD的中点F,且与边BC的延长线交于点E.
(1)若AB = 6,求BE的长;
(2)如图(2),连接BF,过点D作DG⊥AE于点H,交AB于点G. 求证:四边形BFDG是平行四边形.
E D F c
D F c
A G B
图(2)
(1)若AB = 6,求BE的长;
(2)如图(2),连接BF,过点D作DG⊥AE于点H,交AB于点G. 求证:四边形BFDG是平行四边形.
E
 D F c
D F c A G B
图(2)
答案:
(1)【解】
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAF = ∠E.
∵AE是∠BAD的平分线,
∴∠DAF = ∠BAE,
∴∠BAE = ∠E,
∴BE = AB = 6.
(2)【证明】
∵四边形ABCD是平行四边形,
∴AB//CD,AD//BC,
∴∠DAF = ∠E.
∵F是CD的中点,
∴DF = CF. 在△ADF和△ECF中,$\begin{cases}∠DAF = ∠E, \\∠AFD = ∠EFC, \\DF = CF,\end{cases}$
∴△ADF≌△ECF(AAS),
∴AF = EF. 由
(1)可知,BE = AB,
∴BF⊥AE.
∵DG⊥AE,
∴DG//BF. 又
∵DF//BG,
∴四边形BFDG是平行四边形.
(1)【解】
∵四边形ABCD是平行四边形,
∴AD//BC,
∴∠DAF = ∠E.
∵AE是∠BAD的平分线,
∴∠DAF = ∠BAE,
∴∠BAE = ∠E,
∴BE = AB = 6.
(2)【证明】
∵四边形ABCD是平行四边形,
∴AB//CD,AD//BC,
∴∠DAF = ∠E.
∵F是CD的中点,
∴DF = CF. 在△ADF和△ECF中,$\begin{cases}∠DAF = ∠E, \\∠AFD = ∠EFC, \\DF = CF,\end{cases}$
∴△ADF≌△ECF(AAS),
∴AF = EF. 由
(1)可知,BE = AB,
∴BF⊥AE.
∵DG⊥AE,
∴DG//BF. 又
∵DF//BG,
∴四边形BFDG是平行四边形.
4[2024陕西渭南期末,较难]问题背景:
如图,在等边△ABC中,D,E两点分别在边BC,AC上,BD = CE,以AD为边作等边△ADF,连接BE,EF,CF.
问题探究:
(1)求证:△CEF为等边三角形;
(2)求证:四边形BDFE为平行四边形;
(3)若EF = 2,求四边形BDFE的面积.
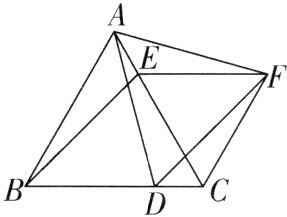
如图,在等边△ABC中,D,E两点分别在边BC,AC上,BD = CE,以AD为边作等边△ADF,连接BE,EF,CF.
问题探究:
(1)求证:△CEF为等边三角形;
(2)求证:四边形BDFE为平行四边形;
(3)若EF = 2,求四边形BDFE的面积.

答案:
(1)【证明】
∵△ABC是等边三角形,
∴AB = AC,∠BAC = ∠ACB = ∠ABC = 60°.
∵△ADF是等边三角形,
∴AD = AF,∠DAF = 60°,
∴∠BAC - ∠DAC = ∠DAF - ∠DAC,即∠BAD = ∠CAF. 在△BAD和△CAF中,$\begin{cases}BA = CA, \\∠BAD = ∠CAF, \\AD = AF,\end{cases}$
∴△BAD≌△CAF(SAS),
∴∠ACF = ∠ABD = 60°,BD = CF. 又
∵BD = CE,
∴CF = CE,
∴△CEF是等边三角形.
(2)【证明】由
(1)可知,△CEF是等边三角形,
∴∠CEF = 60°,EF = CE.
思路分析:
(3)过E作EG⊥BC于G,则∠EGC = 90°,在Rt△CEG中,求得∠CEG = 30°,则CG = $\frac{1}{2}$CE,由勾股定理求得EG的长度,进而即可得解.
思路分析:
(1)由非负数的性质求出a,b的值,再根据三角形ABP的面积等于平行四边形ABCD面积的四分之一列方程,解之即可.
∴∠BCA = ∠CEF = 60°,
∴EF//BD.
∵BD = CE,
∴EF = BD,
∴四边形BDFE为平行四边形.
(3)【解】如图,过E作EG⊥BC于G,则∠EGC = 90°.
∵CE = EF = 2,∠ACB = 60°,
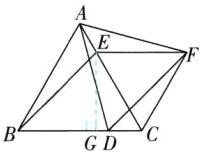
∴在Rt△CEG中,∠CEG = 90° - ∠ACB = 30°,
∴CG = $\frac{1}{2}$CE = 1,
∴EG = $\sqrt{CE^{2}-CG^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$,
∴S_{平行四边形BDFE}=BD·EG = 2×$\sqrt{3}$ = 2$\sqrt{3}$.
(1)【证明】
∵△ABC是等边三角形,
∴AB = AC,∠BAC = ∠ACB = ∠ABC = 60°.
∵△ADF是等边三角形,
∴AD = AF,∠DAF = 60°,
∴∠BAC - ∠DAC = ∠DAF - ∠DAC,即∠BAD = ∠CAF. 在△BAD和△CAF中,$\begin{cases}BA = CA, \\∠BAD = ∠CAF, \\AD = AF,\end{cases}$
∴△BAD≌△CAF(SAS),
∴∠ACF = ∠ABD = 60°,BD = CF. 又
∵BD = CE,
∴CF = CE,
∴△CEF是等边三角形.
(2)【证明】由
(1)可知,△CEF是等边三角形,
∴∠CEF = 60°,EF = CE.
思路分析:
(3)过E作EG⊥BC于G,则∠EGC = 90°,在Rt△CEG中,求得∠CEG = 30°,则CG = $\frac{1}{2}$CE,由勾股定理求得EG的长度,进而即可得解.
思路分析:
(1)由非负数的性质求出a,b的值,再根据三角形ABP的面积等于平行四边形ABCD面积的四分之一列方程,解之即可.
∴∠BCA = ∠CEF = 60°,
∴EF//BD.
∵BD = CE,
∴EF = BD,
∴四边形BDFE为平行四边形.
(3)【解】如图,过E作EG⊥BC于G,则∠EGC = 90°.
∵CE = EF = 2,∠ACB = 60°,

∴在Rt△CEG中,∠CEG = 90° - ∠ACB = 30°,
∴CG = $\frac{1}{2}$CE = 1,
∴EG = $\sqrt{CE^{2}-CG^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$,
∴S_{平行四边形BDFE}=BD·EG = 2×$\sqrt{3}$ = 2$\sqrt{3}$.
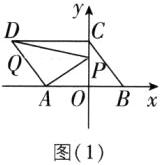
5[较难]在平面直角坐标系中,O为坐标原点,已知两点A(a,0),B(b,0),且a,b满足|a + 4| + (b - 3)² = 0,CD//AB,且CD = AB,点C(0,4)在y轴上.
(1)如图(1),动点P从C点出发,以每秒2个单位长度沿y轴向下运动,当时间t为何值时,三角形ABP的面积等于四边形ABCD面积的四分之一;
(2)如图(2),动点P从O点出发,沿y轴向上运动,连接PD,PA,∠CDP,∠APD,∠PAB之间存在什么样的数量关系?请说明理由(排除P与O,C两点重合的特殊情况).
 D y
D y
AO Bx 图(2)
(1)如图(1),动点P从C点出发,以每秒2个单位长度沿y轴向下运动,当时间t为何值时,三角形ABP的面积等于四边形ABCD面积的四分之一;
(2)如图(2),动点P从O点出发,沿y轴向上运动,连接PD,PA,∠CDP,∠APD,∠PAB之间存在什么样的数量关系?请说明理由(排除P与O,C两点重合的特殊情况).
 D y
D y AO Bx 图(2)
答案:
【解】
(1)
∵|a + 4|+(b - 3)² = 0,
∴a + 4 = 0,b - 3 = 0,
∴a = - 4,b = 3,
∴A(-4,0),B(3,0),
∴OA = 4,OB = 3,
∴AB = 7.
∵点C(0,4),
∴OC = 4.
∵CD//AB,且CD = AB,
∴四边形ABCD是平行四边形.
∵三角形ABP的面积等于平行四边形ABCD面积的四分之一,当点P在x轴上方时,OP = 4 - 2t,
∴$\frac{1}{2}$×(4 - 2t)×7 = $\frac{1}{4}$×7×4,解得t = 1;当点P在x轴的下方时,OP = 2t - 4,
∴$\frac{1}{2}$×(2t - 4)×7 = $\frac{1}{4}$×7×4,解得t = 3. 故当时间t为1或3时,三角形ABP的面积等于四边形ABCD面积的四分之一.
(2)如图
(1),当点P在CD下方时,∠DPA = ∠CDP + ∠PAB. 理由:过P作PQ//DC交AD于Q,
∴∠QPD = ∠CDP.
∵CD//AB,
∴PQ//AB,
∴∠QPA = ∠PAB.
∵∠DPA = ∠QPD + ∠QPA,
∴∠DPA = ∠CDP + ∠PAB. 如图
(2),当点P在CD的上方时,∠DPA = ∠PAB - ∠CDP. 理由:如图
(2),过P作PH//CD,
∴∠HPD = ∠CDP.
∵CD//AB,
∴PH//AB,
∴∠HPA = ∠PAB.
∵∠DPA = ∠HPA - ∠HPD,
∴∠DPA = ∠PAB - ∠CDP.

图
(1) 图
(2)
【解】
(1)
∵|a + 4|+(b - 3)² = 0,
∴a + 4 = 0,b - 3 = 0,
∴a = - 4,b = 3,
∴A(-4,0),B(3,0),
∴OA = 4,OB = 3,
∴AB = 7.
∵点C(0,4),
∴OC = 4.
∵CD//AB,且CD = AB,
∴四边形ABCD是平行四边形.
∵三角形ABP的面积等于平行四边形ABCD面积的四分之一,当点P在x轴上方时,OP = 4 - 2t,
∴$\frac{1}{2}$×(4 - 2t)×7 = $\frac{1}{4}$×7×4,解得t = 1;当点P在x轴的下方时,OP = 2t - 4,
∴$\frac{1}{2}$×(2t - 4)×7 = $\frac{1}{4}$×7×4,解得t = 3. 故当时间t为1或3时,三角形ABP的面积等于四边形ABCD面积的四分之一.
(2)如图
(1),当点P在CD下方时,∠DPA = ∠CDP + ∠PAB. 理由:过P作PQ//DC交AD于Q,
∴∠QPD = ∠CDP.
∵CD//AB,
∴PQ//AB,
∴∠QPA = ∠PAB.
∵∠DPA = ∠QPD + ∠QPA,
∴∠DPA = ∠CDP + ∠PAB. 如图
(2),当点P在CD的上方时,∠DPA = ∠PAB - ∠CDP. 理由:如图
(2),过P作PH//CD,
∴∠HPD = ∠CDP.
∵CD//AB,
∴PH//AB,
∴∠HPA = ∠PAB.
∵∠DPA = ∠HPA - ∠HPD,
∴∠DPA = ∠PAB - ∠CDP.


图
(1) 图
(2)
查看更多完整答案,请扫码查看


