《2025年初中必刷题八年级数学下册苏科版》

1[2024江苏连云港期中，中]如图，菱形ABCD的对角线交于点O，AB = 5，AC = 6，DE⊥BC于点E，连接OE，则OE的长为（ ）

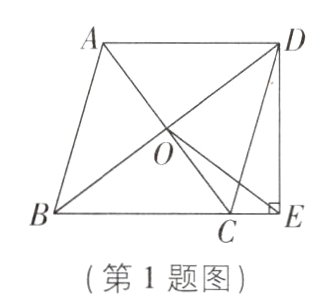
A. 3
B. 4
C. 4.5
D. 5

答案： B　[解析]
∵四边形ABCD是菱形，
∴AD = AB = 5,AC⊥BD,AO = $\frac{1}{2}$AC = $\frac{1}{2}$×6 = 3,OB = OD.在Rt△AOD中，由勾股定理得OD = $\sqrt{AD^{2}-AO^{2}}$ = $\sqrt{25 - 9}$ = 4,
∴BD = 2OD = 8.
∵DE⊥BC,
∴∠DEB = 90°.
∵OD = OB,
∴OE = $\frac{1}{2}$BD = $\frac{1}{2}$×8 = 4.

2[2023江苏苏州吴江区调研，中]如图，在菱形ABCD中，AB = 3，过点A作AE⊥BC于点E，交BD于点F，点G为DF的中点.若∠BAG = 90°，则AG的长为（ ）

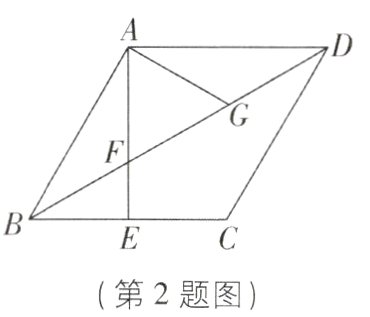
A. √3/3
B. 1
C. 3/2
D. √3

答案： D　[解析]
∵四边形ABCD为菱形，
∴AD//BC,AB = AD,
∴∠ABD = ∠ADB.
∵AE⊥BC,
∴AE⊥AD.
∵点G为DF的中点，
∴AG = DG,
∴∠GAD = ∠GDA,
∴∠AGB = 2∠ADB.
∵∠BAG = 90°,
∴∠AGB + ∠ABG = 2∠ADB + ∠ABG = 3∠ABG = 90°,
∴∠ABG = 30°,
∴BG = 2AG.在Rt△BAG中,$AB^{2}+AG^{2}=BG^{2}$,即$3^{2}+AG^{2}=(2AG)^{2}$,
∴AG = $\sqrt{3}$.故选D.

3[中]如图，在菱形ABCD中，AB的垂直平分线交对角线BD于点F，垂足为点E，连接AF，AC.若∠DCB = 80°，则∠FAC = ________.

答案： 10°　[解析]
∵EF是线段AB的垂直平分线，
∴AF = BF,
∴∠FAB = ∠FBA.
∵四边形ABCD是菱形，∠DCB = 80°,
∴BC = AB,AC⊥BD,∠BCA = $\frac{1}{2}$∠DCB = 40°,
∴∠BAC = ∠BCA = 40°,
∴∠FBA = 90° - ∠BAC = 50°,
∴∠FAB = 50°,
∴∠FAC = ∠FAB - ∠BAC = 50° - 40° = 10°,故答案为10°.

4新考法[2024陕西西安雁塔区模拟，中]小方在学习菱形时，发现可以利用菱形纸片拼出著名的“赵爽弦图”：把图(1)中的菱形沿对角线分成四个全等的直角三角形，这四个直角三角形可以拼出如图(2)所示的面积为7的正方形ABCD和如图(3)所示的边长为1的正方形EFGH，则图(1)中菱形的边长为________.

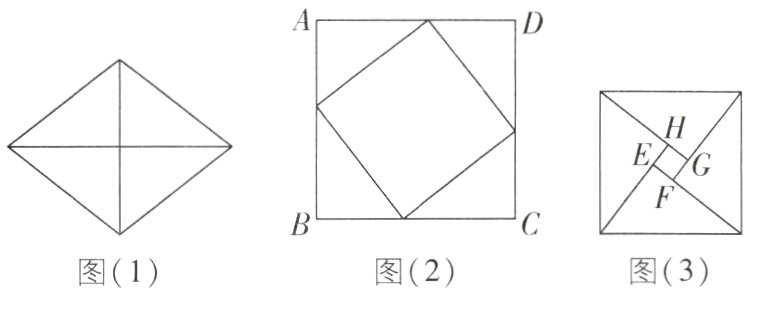
答案： 4.2　[解析]设菱形中直角三角形的较长的直角边长为a，较短的直角边长为b，则$\begin{cases}(a + b)^{2}=7\\(a - b)^{2}=1\end{cases}$，化简得ab = $\frac{3}{2}$,
∴ $a^{2}+b^{2}=(a + b)^{2}-2ab = 7 - 3 = 4$,
∴菱形的边长为$\sqrt{a^{2}+b^{2}}$ = 2.

5[2024江苏苏州工业园区校级期中，中]如图，四边形ABCD为菱形，∠ABC = 70°，延长BC到E，在∠DCE内作射线CM，使得∠ECM = 15°，过点D作DF⊥CM，垂足为F.若DF = √10，则对角线BD的长为________.

答案：
$2\sqrt{10}$　[解析]如图，连接AC交BD于点H.
∵四边形ABCD是菱形，∠ABC = 70°,
∴BH = DH,AC⊥BD,CB = CD,∠CBD = $\frac{1}{2}$∠ABC = 35°,AB//CD,
∴∠DHC = 90°,∠CDB = ∠CBD = 35°,∠DCE = ∠ABC = 70°.
∵∠ECM = 15°,
∴∠DCF = ∠DCE - ∠ECM = 70° - 15° = 55°.
∵DF⊥CM,
∴∠DFC = 90°,
∴∠CDF = 90° - ∠DCF = 35°,
∴∠CDH = ∠CDF.在△CDH和△CDF中,$\begin{cases}\angle DHC = \angle DFC = 90^{\circ}\\\angle CDH = \angle CDF\\CD = CD\end{cases}$,
∴△CDH≌△CDF(AAS),
∴DH = DF = $\sqrt{10}$,
∴BD = 2DH = $2\sqrt{10}$,故答案为$2\sqrt{10}$.

6[较难]如图，在菱形ABCD中，AE⊥BC于点E.作AF⊥CD于点F，连接EF，BD.
(1)求证：EF//BD；
(2)设AE与对角线BD相交于点G，若CE = 4，BE = 6，四边形CDGE和△AGD的面积分别是S₁和S₂，求S₁ - S₂的值.

答案：

(1)[证明]
∵四边形ABCD是菱形，
∴∠ABE = ∠ADF,AB = AD = BC = CD.
∵AE⊥BC,AF⊥CD,
∴∠AEB = ∠AFD = 90°.在△ABE和△ADF中,$\begin{cases}\angle AEB = \angle AFD\\\angle ABE = \angle ADF\\AB = AD\end{cases}$,
∴△ABE≌△ADF(AAS),
∴BE = DF.
∵BC = CD,
∴∠CBD = ∠CDB,CE = CF,
∴∠CEF = ∠CFE,
∴∠CEF = ∠CBD = $\frac{1}{2}(180^{\circ}-\angle C)$,
∴EF//BD.
(2)[解]连接CG，如图所示.
∵四边形ABCD是菱形，
∴∠ADG = ∠CDG,AD = CD.在△ADG和△CDG中,$\begin{cases}AD = CD\\\angle ADG = \angle CDG\\DG = DG\end{cases}$,
∴△ADG≌△CDG(SAS),
∴AG = CG,△ADG和△CDG的面积相等，
∴ $S_{1}-S_{2}=S_{\triangle CGE}$.
∵四边形ABCD是菱形，
∴AB = BC = CE + BE = 4 + 6 = 10.
∵AE⊥BC，
∴AE = $\sqrt{AB^{2}-BE^{2}}$ = 8.设EG = x，则AG = CG = 8 - x.在Rt△CEG中,$EG^{2}+EC^{2}=CG^{2}$,即$x^{2}+4^{2}=(8 - x)^{2}$,解得x = 3，即EG = 3,
∴ $S_{1}-S_{2}=S_{\triangle CGE}=\frac{1}{2}CE\cdot EG=\frac{1}{2}\times4\times3 = 6$.

7核心素养·推理能力[较难]如图，菱形ABCD中，AB = 5，∠ABC = 60°，∠EAF = 60°，∠EAF的两边分别交直线BC，CD于点E，F.
(1)如图(1)所示，当点E，F分别在边BC，CD上时，求CE + CF的值；
(2)如图(2)所示，当点E，F分别在CB，DC的延长线上时，CE，CF又存在怎样的数量关系?证明你的结论.

答案：
[解]
(1)如图
(1)，连接AC.
∵四边形ABCD是菱形，∠B = 60°，
∴△ABC，△ACD都是等边三角形，
∴∠BAC = 60°，AB = AC = BC = 5，∠ACD = 60°.
∵∠EAF = 60°，
∴∠BAC - ∠CAE = ∠EAF - ∠CAE，即∠BAE = ∠CAF.又
∵AB = AC，∠B = ∠ACF = 60°，
∴△ABE≌△ACF(ASA)，
∴BE = CF，
∴CE + CF = CE + BE = BC = 5.
(2)CE - CF = 5. 证明：如图
(2)，连接AC. 由
(1)得△ABC，△ACD都是等边三角形，
∴∠BAC = ∠ACD = 60°，AB = AC = BC = 5.
∵∠EAB = 60° - ∠BAF，∠CAF = 60° - ∠BAF，
∴ ∠EAB = ∠FAC.
∵ AB = AC，∠ABE = ∠ACF = 120°，
∴ △ABE≌△ACF(ASA)，
∴ BE = CF，
∴ CE - CF = CE - BE = BC = 5.