《2025年初中必刷题八年级数学下册苏科版》

1[2023江苏扬州邗江区调研，中]若反比例函数的图像经过点$A(a - b,a)$，其中$a$，$b$为实数，则这个反比例函数的图像一定经过点 （ ）
A. $(b,a - b)$
B. $(b - a,a)$
C. $(a,a - b)$
D. $(a - b,b)$

答案： 刷提升
1. C 【解析】设该反比例函数的关系式为y=$\frac{k}{x}$（k≠0）。
∵该反比例函数的图像经过点A(a−b,a)，
∴k=a(a−b)，只有C选项的点的横、纵坐标的积为a(a−b)。故选C。

2[2023江苏南京秦淮区期末，中]如图，在平面直角坐标系中，将一块含有$45^{\circ}$角的直角三角板按如图所示的方式放置，直角顶点$C$的坐标为$(2,0)$，顶点$A$的坐标为$(0,4)$，顶点$B$恰好落在第一象限内，反比例函数$y=\frac{k}{x}(x＞0)$的图像经过点$B$，则$k$的值为 （ ）


A. 4
B. 6
C. 8
D. 12

答案： 刷提升
2. D 【解析】过点B作BD⊥x轴于点D。由题意可知，AC=BC，∠ACB=∠AOC=90°，
∴∠ACO+∠BCD=90°，∠OAC+∠ACO=90°，
∴∠OAC=∠BCD。又
∵∠AOC=∠BDC=90°，AC=CB，
∴△ACO≌△CBD（AAS），
∴OC=BD，OA=CD。
∵A(0,4)，C(2,0)，
∴OA=4，OC=2，
∴OD=6，BD=2，
∴B(6,2)。
∵反比例函数y=$\frac{k}{x}$的图像经过点B，
∴k=6×2=12。故选D。

3[2024新疆乌鲁木齐二模，中]如图，在$Rt\triangle AOB$中，$\angle AOB = 90^{\circ}$，$OB = 4$，$AB// x$轴，双曲线$y=\frac{k}{x}$经过点$B$，将$\triangle AOB$绕点$B$逆时针旋转，使点$O$的对应点$D$恰好落在$x$轴正半轴上，$AB$的对应线段$CB$恰好经过点$O$，则$k$的值是________.

答案： 刷提升
3. 4$\sqrt{3}$ 【解析】
∵AB//x轴，
∴∠ABO=∠BOD。由旋转的性质可得，∠ABO=∠CBD，OB=BD，
∴∠BOD=∠OBD，
∴BD=OD，即BD=OB=OD，
∴△BOD是等边三角形，
∴∠OBD=60°。过点B作BE⊥OD于点E，
∴∠OBE=$\frac{1}{2}$∠OBD=30°，
∴OE=$\frac{1}{2}$OB=2，
∴BE=2$\sqrt{3}$，
∴B(2,2$\sqrt{3}$)。
∵双曲线y=$\frac{k}{x}$经过点B，
∴k=2×2$\sqrt{3}$=4$\sqrt{3}$。故答案为4$\sqrt{3}$。

4[2024四川南充模拟，中]如图，点$A$在双曲线$y=\frac{a}{x}(x＜0)$上，过点$A$作$AD\perp x$轴于点$D$，与双曲线$y=\frac{b}{x}(x＜0)$交于点$B$，点$C$是$OA$的中点，若$\triangle ABC$的面积为$3$，则$1 - 2a + 2b$的值为________.

答案： 刷提升
4. 25 【解析】连接OB。
∵点C是OA的中点，
∴S△ABC=$\frac{1}{2}$S△AOB=3，
∴S△AOB=6。
∵A、B分别在双曲线y=$\frac{a}{x}$（x＜0）、y=$\frac{b}{x}$（x＜0）上，AD⊥x轴，
∴设A(m,$\frac{a}{m}$)，B(m,$\frac{b}{m}$)，
∴OD=−m，AB=AD−BD=$\frac{a}{m}$−$\frac{b}{m}$。
∵S△AOB=$\frac{1}{2}$AB×OD=6，
∴$\frac{1}{2}$($\frac{a}{m}$−$\frac{b}{m}$)×(−m)=6，
∴−a+b=12，
∴1−2a+2b=1+2(−a+b)=1+2×12=25。故答案为25。

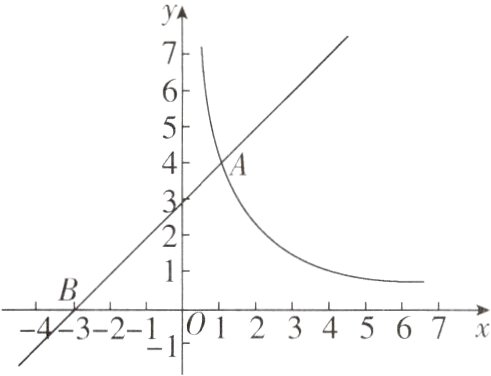
5[中]如图，在平面直角坐标系$xOy$中，直线$y = x + 3$与反比例函数$y=\frac{k}{x}(x＞0)$的图像交于点$A(1,m)$，与$x$轴交于点$B$.
(1)求$m$，$k$的值.
(2)过动点$P(0,n)$作平行于$x$轴的直线，交反比例函数$y=\frac{k}{x}(x＞0)$的图像于点$C$，交直线$y = x + 3$于点$D$，点$C$在点$D$右侧，当$CD = 3$时，求$n$的值.

答案： 刷提升
5. 【解】
(1)
∵直线y=x+3经过点A(1,m)，
∴m=1+3=4。
∵反比例函数y=$\frac{k}{x}$（x＞0）的图像经过点A(1,4)，
∴k=1×4=4。
(2)由
(1)知，反比例函数表达式为y=$\frac{4}{x}$（x＞0）。
∵点P的坐标为(0,n)，
∴点C的坐标为($\frac{4}{n}$,n)，点D的坐标为(n−3,n)。
∵CD=3，点C在点D右侧，
∴$\frac{4}{n}$−(n−3)=3，解得n=2或n=−2。经检验，n=2或n=−2均是原方程的解。
∵y=$\frac{4}{x}$（x＞0），
∴n=2。

6核心素养·模型观念[难]如图，点$M(0,m)$为$y$轴上一点，$m＜0$，过点$M$作$y$轴的垂线$l$，与反比例函数$y=\frac{1}{x}$的图像交于点$P$. 把直线$l$下方反比例函数的图像沿着直线$l$翻折，其他部分保持不变，所形成的新图像称为“$G$图像”.
(1)当$m = -1$时，求“$G$图像”与$x$轴的交点横坐标.
(2)过$y$轴上另一点$N(0,n)$作$y$轴垂线，与“$G$图像”交于点$A$，$B$.
①若$n = 2$，且$AN = 2BN$，求$m$的值；
②若$AN = 2BN$，求$m$与$n$的数量关系.

答案：
刷素养
6. 【解】
(1)当m=−1时，M(0,−1)。
∵“G图像”与x轴的交点纵坐标为0，则它关于直线l对称点的纵坐标为−2，
∴把y=−2代入y=$\frac{1}{x}$，得x=−$\frac{1}{2}$，
∴“G图像”与x轴的交点横坐标为−$\frac{1}{2}$。
(2)①由题知，N(0,2)，则点A和点B的纵坐标都是2。当点A在y轴的右侧，点B在y轴的左侧时，如图
(1)。
∵点A在反比例函数的图像上，
∴点A的横坐标为$\frac{1}{2}$，则A($\frac{1}{2}$,2)，
∴AN=$\frac{1}{2}$。
∵AN=2BN，
∴点B的横坐标为−$\frac{1}{4}$，则B(−$\frac{1}{4}$,2)。根据题意知，点B关于直线y=m的对称点B'的坐标为(−$\frac{1}{4}$,m−(2−m))，且点B'在反比例函数y=$\frac{1}{x}$的图像上，
∴−$\frac{1}{4}$×(2m−2)=1，解得m=−1。当点A在y轴的左侧，点B在y轴的右侧时，如图
(2)。
∵点B在反比例函数的图像上，
∴点B的横坐标为$\frac{1}{2}$，则B($\frac{1}{2}$,2)，
∴BN=$\frac{1}{2}$。
∵AN=2BN，
∴点A的横坐标为−1，则A(−1,2)。根据题意知，点A关于直线y=m的对称点A'的坐标为(−1,m−(2−m))，且点A'在反比例函数图像上，
∴−(2m−2)=1，解得m=$\frac{1}{2}$＞0，与题中m＜0的条件矛盾，
∴不符合题意，舍去。综上所述，m的值为−1。


②由题知，N(0,n)，则点A和点B的纵坐标都是n。当n＞0，点A在y轴的右侧，点B在y轴的左侧时，如图
(1)。
∵点A在反比例函数的图像上，
∴点A的横坐标为$\frac{1}{n}$，则A($\frac{1}{n}$,n)，
∴AN=$\frac{1}{n}$。
∵AN=2BN，
∴点B的横坐标为−$\frac{1}{2n}$，则B(−$\frac{1}{2n}$,n)。根据题意知，点B关于直线y=m的对称点B'的坐标为(−$\frac{1}{2n}$,m−(n−m))，且点B'在反比例函数图像上，
∴−$\frac{1}{2n}$(2m−n)=1，
∴m=−$\frac{1}{2}$n。当n＞0，点A在y轴的左侧，点B在y轴的右侧时，如图
(2)。
∵点B在反比例函数的图像上，
∴点B的横坐标为$\frac{1}{n}$，则B($\frac{1}{n}$,n)，
∴BN=$\frac{1}{n}$。
∵AN=2BN，
∴点A的横坐标为−$\frac{2}{n}$，则A(−$\frac{2}{n}$,n)。根据题意知，点A关于直线y=m的对称点A'的坐标为(−$\frac{2}{n}$,m−(n−m))，且点A'在反比例函数图像上，
∴−$\frac{2}{n}$(2m−n)=1，
∴m=$\frac{1}{4}$n。
∵n＞0，
∴m＞0，与题中的m＜0的条件矛盾，
∴不符合题意，舍去。如图
(3)，当m＜n＜0时，点A和点B在第三象限。又
∵AN=2BN，
∴点A在点B的左侧。
∵点A在反比例函数的图像上，
∴点A的横坐标为$\frac{1}{n}$，则A($\frac{1}{n}$,n)。
∵n＜0，
∴AN=−$\frac{1}{n}$。
∵AN=2BN，
∴点B的横坐标为$\frac{1}{2n}$，则B($\frac{1}{2n}$,n)。根据题意知，点B关于直线y=m的对称点B'的坐标为($\frac{1}{2n}$,m−(n−m))，且点B'在反比例函数图像上，
∴$\frac{1}{2n}$(2m−n)=1，
∴m=$\frac{3}{2}$n。综上所述，m与n的数量关系为m=−$\frac{1}{2}$n或m=$\frac{3}{2}$n。

关键点拨
(2)②分情况讨论：当n＞0，点A在y轴的右侧，点B在y轴的左侧时；当n＞0，点A在y轴的左侧，点B在y轴的右侧时；当m＜n＜0时。
关键点拨
由x₁＜0＜x₂时，y₁＜y₂得到2024−k＞0是解题关键。