《2025年初中必刷题八年级数学下册苏科版》

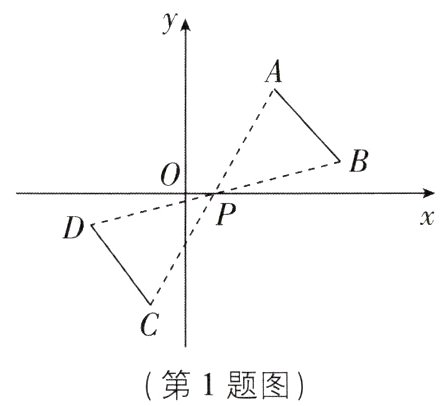
1[2023湖北黄石期末，中]如图，线段AB与线段CD关于点P成中心对称，若点A(a,b)，B(5,1)，D( - 3, - 1)，则点C的坐标为（ ）

A. ( - a, - b)
B. ( - a + 2, - b)
C. ( - a - 1, - b + 1)
D. ( - a + 1, - b - 1)

答案： B【解析】设C(m,n).
∵线段AB与线段CD关于点P成中心对称，
∴点P为线段AC，BD的中点，
∴$\frac{a + m}{2}=\frac{5 - 3}{2}$，$\frac{b + n}{2}=\frac{1 - 1}{2}$，
∴m = -a + 2，n = -b，
∴C(-a + 2,-b)，故选B.

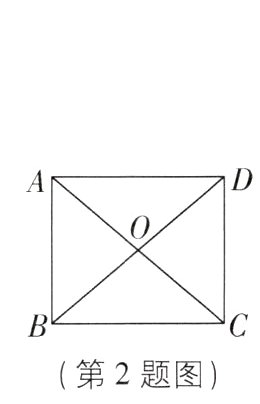
2新情境[2024江苏连云港质检，中]如图，△AOD与△COB关于点O成中心对称，连接AB，CD，以下结论错误的是（ ）

A. OA=OB
B. △AOD≌△COB
C. AD=BC
D. S△ACD = S△BCD

答案： A【解析】OA与OB不一定相等，故选项A错误；
∵△AOD与△COB关于点O成中心对称，
∴△AOD≌△COB，故选项B正确；
∵△AOD≌△COB，
∴AD = BC，故选项C正确；
∵△AOD≌△COB，
∴$S_{\triangle AOD}=S_{\triangle COB}$，
∴$S_{\triangle AOD}+S_{\triangle COD}=S_{\triangle COB}+S_{\triangle COD}$，即$S_{\triangle ACD}=S_{\triangle BCD}$，故选项D正确.

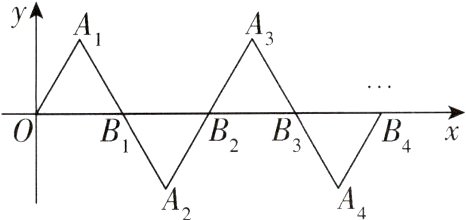
3[2024山东济宁一模，较难]如图，平面直角坐标系中，△OA₁B₁是边长为2的等边三角形，作△B₁A₂B₂与△B₁A₁O关于点B₁成中心对称，再作△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，…，如此作下去，则△B₂ₙ₋₁A₂ₙB₂ₙ(n是正整数)的顶点A₂ₙ的坐标是（ ）

A. (4n - 1, - $\sqrt{3}$)
B. (4n - 1,$\sqrt{3}$)
C. (4n + 1, - $\sqrt{3}$)
D. (4n + 1,$\sqrt{3}$)

答案： A【解析】
∵△OA₁B₁是边长为2的等边三角形，
∴A₁的坐标为(1,$\sqrt{3}$)，B₁的坐标为(2,0).
∵△B₁A₂B₂与△B₁A₁O关于点B₁成中心对称，
∴点A₂与点A₁关于点B₁成中心对称，
∴点A₂的坐标是(3,-$\sqrt{3}$).
∵△B₂A₃B₃与△B₂A₂B₁关于点B₂成中心对称，
∴点A₃与点A₂关于点B₂成中心对称，
∴点A₃的坐标是(5,$\sqrt{3}$).
∵△B₃A₄B₄与△B₃A₃B₂关于点B₃成中心对称，
∴点A₄与点A₃关于点B₃成中心对称，
∴点A₄的坐标是(7,-$\sqrt{3}$)，…，
∵1 = 2×1 - 1，3 = 2×2 - 1，5 = 2×3 - 1，7 = 2×4 - 1，…，
∴Aₙ的横坐标是2n - 1，
∴A₂ₙ的横坐标是2×2n - 1 = 4n - 1.
∵当n为奇数时，Aₙ的纵坐标是$\sqrt{3}$，当n为偶数时，Aₙ的纵坐标是-$\sqrt{3}$，
∴A₂ₙ的纵坐标是-$\sqrt{3}$，
∴顶点A₂ₙ的坐标是(4n - 1,-$\sqrt{3}$). 故选A.

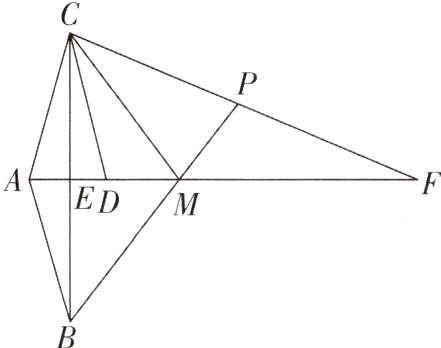
4[2023江苏盐城调研，中]如图，△ABM与△ACM关于直线AF成轴对称，△ABE与△DCE关于点E成中心对称，点E，D，M都在线段AF上，BM的延长线交CF于点P.
(1)求证：AC = CD；
(2)若∠BAC = 2∠MPC，请你判断∠F与∠MCD的数量关系，并说明理由.

答案：
(1)【证明】
∵△ABM与△ACM关于直线AF成轴对称，
∴△ABM≌△ACM，
∴AB = AC. 又
∵△ABE与△DCE关于点E成中心对称，
∴△ABE≌△DCE，
∴AB = CD，
∴AC = CD.
(2)【解】∠F = ∠MCD. 理由：由
(1)可得∠BAE = ∠CAE = ∠CDE，∠CMA = ∠BMA. 又
∵∠BAC = 2∠MPC，∠BMA = ∠PMF，
∴设∠MPC = α，则∠BAE = ∠CAE = ∠CDE = α. 设∠BMA = β，则∠PMF = ∠CMA = β，
∴∠F = ∠CPM - ∠PMF = α - β，∠MCD = ∠CDE - ∠DMC = α - β，
∴∠F = ∠MCD.

5核心素养·几何直观[难]课外兴趣小组活动时，老师提出了如下问题：
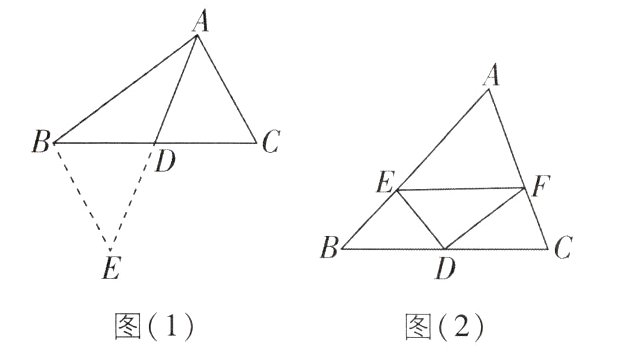
如图(1)，在△ABC中，若AB = 5，AC = 3，求BC边上的中线AD的取值范围.
小明在组内经过讨论，最终得到了如下的解决方法：延长AD到E，使得DE = AD，再连接BE（或将△ACD绕点D逆时针旋转180°得到△EBD），把AB，AC，2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，即1＜AD＜4.
感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中.
解决问题：受到上述问题的启发，请你证明下列命题：(1)如图(2)，在△ABC中，D是BC边的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF. 求证：BE + CF＞EF.
(2)在(1)的条件下，若∠A = 90°，探索线段BE，CF，EF之间的等量关系，并加以证明.

答案：

(1)【证明】如图，延长FD到G，使得DG = DF，连接BG，EG(或把△CFD绕点D逆时针旋转180°得到△BGD，连接EG)，易证△CFD≌△BGD，
∴CF = BG.

∵DE⊥DF，DF = DG，
∴EF = EG.
在△BEG中，BE + BG ＞ EG，即BE + CF ＞ EF.
(2)【解】等量关系为$BE^{2}+CF^{2}=EF^{2}$.
证明：若∠A = 90°，则∠EBC + ∠C = 90°.
由
(1)得EF = EG. 由△CFD≌△BGD得∠C = ∠DBG，CF = BG，
∴∠EBC + ∠DBG = 90°，即∠EBG = 90°.
在Rt△EBG中，$BE^{2}+BG^{2}=EG^{2}$，
∴$BE^{2}+CF^{2}=EF^{2}$.