《2025年初中必刷题八年级数学下册苏科版》

1[2024江苏南通调研]下列命题正确的是(　　　)
A. 矩形的四个角都相等
B. 矩形的四条边都相等
C. 矩形的对角线互相垂直
D. 矩形的对角线平分内角

答案： A　[解析]A选项，矩形的四个角都相等，原命题正确，符合题意;B选项，矩形的四条边不相等，故原命题错误，不符合题意;C选项，矩形的对角线相等但不垂直，故原命题错误，不符合题意;D选项，矩形的对角线相等但不平分内角，故原命题错误，不符合题意.故选A.

2[2024江苏宿迁期末]如图,直线a//b,线段AB和矩形CDEF在直线a,b之间,点A,E分别在a,b上,点B,C,F在同一直线上.若∠α = 70°,∠β = 60°,则∠ABC=(　　　)

A. 130°　　
　B. 135°　　
　C. 140°　　
　D. 150°

答案：
C　[解析]分别过点B，F作$l_1// a$，$l_2// a$，如图.
∵$a// b$，
∴$l_1// l_2// a// b$.
∵四边形CDEF是矩形，
∴$\angle 1+\angle 2 = 90^{\circ}$.
∵$l_2// b$，$\angle \beta = 60^{\circ}$，
∴$\angle 1 = \angle \beta = 60^{\circ}$，则$\angle 2 = 90^{\circ}-60^{\circ}=30^{\circ}$.
∵$l_1// l_2$，
∴$\angle 4 = \angle 2 = 30^{\circ}$.
∵$l_1// a$，$\angle \alpha = 70^{\circ}$，
∴$\angle 3 = 180^{\circ}-\angle \alpha = 180^{\circ}-70^{\circ}=110^{\circ}$，
∴$\angle ABC=\angle 3+\angle 4 = 110^{\circ}+30^{\circ}=140^{\circ}$. 故选C.

3[新考法][2023江苏镇江期中]如图,在直角坐标系中,矩形OABC的顶点B的坐标是(1,3),连接AC,则AC的长是(　　　)

A. 3　　　
　B. $\sqrt{7}$　　　
　C. $\sqrt{10}$　　
　D. 4

答案：
C　[解析]如图，连接OB，过B作$BM\perp x$轴于M.
∵点B的坐标是(1,3)，
∴$OM = 1$，$BM = 3$，由勾股定理可得$OB=\sqrt{1^{2}+3^{2}}=\sqrt{10}$.
∵四边形OABC为矩形，
∴$OB = AC$，
∴$AC=\sqrt{10}$. 故选C.

4[2024上海金山区期中]如图,矩形ABCD中,点E,F分别为AD,BC边上的任意点,△ABG,△DCH的面积分别为15和25,那么四边形EGFH的面积为________.

答案： 40　[解析]连接EF.
∵$S_{\triangle ABF}=S_{\triangle EBF}$，
∴$S_{\triangle EFG}=S_{\triangle ABG}=15$. 同理$S_{\triangle EFH}=S_{\triangle DCH}=25$，
∴$S_{四边形EGFH}=S_{\triangle EFG}+S_{\triangle EFH}=15 + 25 = 40$. 故答案为40.

5[2024江苏无锡新吴区期末]如图,在矩形ABCD中,AB = 8,BC = 7,点P在CD上,点Q在AD上,P,Q分别从C,A同时出发,以相同的速度向点D运动,则AP + BQ的最小值为________.

答案：
17　[解析]如图，延长CB至E，使得$CE = AB$，连接PE. 在矩形ABCD中，$AB = 8$，$BC = 7$，
∴$CE = AB = 8$，$\angle PCE=\angle QAB = 90^{\circ}$. 依题意，$AQ = PC$，
∴$\triangle PCE\cong\triangle QAB$，
∴$BQ = PE$. 作点E关于DC的对称点F，连接AF，PF，则$PE = PF = BQ$.
∵$AF\leqslant AP + PF = AP + BQ$，则A，P，F三点共线时，$AP + BQ$取得最小值，
∴$AF=\sqrt{AB^{2}+BF^{2}}=\sqrt{8^{2}+15^{2}} = 17$，
∴$AP + BQ$的最小值为17. 故答案为17.

6[2024吉林四平模拟]如图,将矩形纸片ABCD沿EF折叠后,点D,C分别落在点D',C'的位置,ED'的延长线恰好经过B点.若DE = DC = 6,CF = 4,则AE等于________.

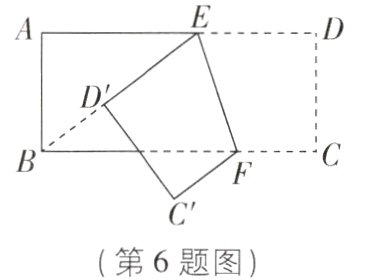
答案： 8　[解析]
∵四边形ABCD是矩形，$DE = DC = 6$，
∴$AB = CD = 6$，$AD = BC$，$AD// BC$，$\angle A = 90^{\circ}$，
∴$\angle BFE=\angle DEF$.
∵将矩形纸片ABCD沿EF折叠后，点D，C分别落在点$D'$，$C'$的位置，$ED'$的延长线恰好经过B点，
∴$\angle BEF=\angle DEF$，
∴$\angle BEF=\angle BFE$，
∴$BF = BE$. 设$AD = BC = x$，
∴$AE = AD - DE = x - 6$，$BE = BF = BC - CF = x - 4$. 在$Rt\triangle ABE$中，$AB^{2}+AE^{2}=BE^{2}$，即$6^{2}+(x - 6)^{2}=(x - 4)^{2}$，解得$x = 14$，
∴$AE = x - 6 = 14 - 6 = 8$. 故答案为8.

7如图,已知矩形ABCD中,点E在边BC的延长线上,且CE = BD,连接AE交BD于F,如果∠E = 20°,那么∠AFB的度数为________.

答案：
$60^{\circ}$ 思路分析：连接AC交BD于点O.由矩形的性质得出AC=BD，OB=OC，则∠OBC=∠OCB，证出AC=CE，则∠CAE=∠E=20°，由三角形的外角性质求出∠OBC=∠OCB=40°，再由三角形的外角性质计算即可得出答案.
[解析]连接AC交BD于点O，如图所示.
∵四边形ABCD是矩形，
∴$AC = BD$，$OB = OC$，
∴$\angle OBC=\angle OCB$.
∵$CE = BD$，
∴$AC = CE$，
∴$\angle CAE=\angle E = 20^{\circ}$，
∴$\angle OBC=\angle OCB=\angle CAE+\angle E = 40^{\circ}$，
∴$\angle AFB=\angle OBC+\angle E = 40^{\circ}+20^{\circ}=60^{\circ}$. 故答案为$60^{\circ}$.

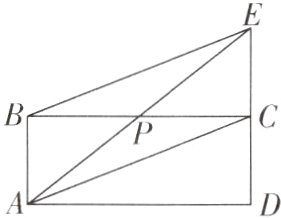
8[2024贵州贵阳模拟]如图,矩形ABCD中,点P是BC边的中点,线段AP的延长线与DC的延长线交于点E.
(1)求证:△ABP≌△ECP;
(2)连接AC,BE,求证:四边形ABEC是平行四边形.

答案： [证明]
(1)
∵四边形ABCD是矩形，
∴$AB// CD$，
∴$\angle ABC=\angle ECP$.
∵点P是BC边的中点，
∴$BP = CP$.
在$\triangle ABP$和$\triangle ECP$中，$\begin{cases}\angle ABC=\angle ECP,\\BP = CP,\\\angle APB=\angle EPC,\end{cases}$
∴$\triangle ABP\cong\triangle ECP$.
(2)
∵四边形ABCD是矩形，
∴$AB// CD$，
∴$AB// CE$.
由
(1)知$\triangle ABP\cong\triangle ECP$，
∴$AB = EC$，
∴四边形ABEC是平行四边形.

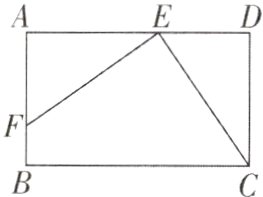
9如图,已知矩形ABCD中,E是AD边上一点,F是AB边上的一点,EF⊥EC,且EF = EC.
(1)求证:△AEF≌△DCE.
(2)若DE = 5 cm,矩形ABCD的周长为38 cm,求AE的长.

答案：
(1)[证明]
∵$EF\perp CE$，
∴$\angle FEC = 90^{\circ}$，
∴$\angle AEF+\angle DEC = 90^{\circ}$.
又
∵$\angle ECD+\angle DEC = 90^{\circ}$，
∴$\angle AEF=\angle ECD$.
∵四边形ABCD是矩形，
∴$\angle A=\angle D = 90^{\circ}$.
在$\triangle AEF$和$\triangle DCE$中，$\angle A=\angle D$，$\angle AEF=\angle ECD$，$EF = EC$，
∴$\triangle AEF\cong\triangle DCE(AAS)$.
(2)[解]
∵$\triangle AEF\cong\triangle DCE$，
∴$AE = CD$，
∴$AD = AE + DE = CD + DE$.
∵矩形ABCD的周长为38 cm，
∴$2(AD + DC)=2(AE + DE + DC)=2(AE + AE + DE)=4AE + 10 = 38$，
∴$AE = 7$ cm.