《2025年初中必刷题八年级数学下册苏科版》

1[2024新疆库尔勒一模]已知分式方程$\frac{x}{x - 2}-\frac{1}{x^{2}-4}=1$，去分母得（ ）
A. $x(x + 2)-1 = 1$
B. $x(x - 2)-1 = x^{2}-4$
C. $x(x + 2)-1 = x^{2}-4$
D. $x - 1 = x^{2}-4$

答案： C [解析]方程两边都乘最简公分母$(x + 2)(x - 2)$，得$x(x + 2) - 1 = (x + 2)(x - 2)$，即$x(x + 2) - 1 = x^{2}-4$。

2[2024安徽合肥模拟]若代数式$\frac{1}{x - 2}$和$\frac{3}{x}$的值互为相反数，则$x$等于（ ）
A. 1
B. $\frac{3}{2}$
C. 2
D. $\frac{2}{3}$

答案： B [解析]根据题意得$\frac{1}{x - 2}+\frac{3}{x}=0$，去分母得$x + 3(x - 2)=0$，解得$x=\frac{3}{2}$，检验：当$x=\frac{3}{2}$时，$x(x - 2)\neq0$，
∴分式方程的解为$x=\frac{3}{2}$。

3新考法[2024辽宁朝阳一模]解分式方程$\frac{2}{x + 1}+\frac{3}{x - 1}=\frac{6}{x^{2}-1}$分以下四步，其中错误的一步是（ ）
A. 方程两边各分式的最简公分母是$(x - 1)(x + 1)$
B. 方程两边都乘$(x - 1)(x + 1)$，得整式方程$2(x - 1)+3(x + 1)=6$
C. 解这个整式方程，得$x = 1$
D. 原方程的解为$x = 1$

答案： D [解析]分式方程的最简公分母为$(x - 1)(x + 1)$，方程两边都乘$(x - 1)(x + 1)$，得整式方程$2(x - 1)+3(x + 1)=6$，解得$x = 1$，经检验，$x = 1$是增根，分式方程无解，故A、B、C选项正确，D选项错误。故选D。

4分式方程$\frac{x + 1}{2x - 1}=1$的解为__________.

答案： $x = 2$ [解析]方程的两边都乘$(2x - 1)$，得$x + 1 = 2x - 1$，解得$x = 2$。检验：当$x = 2$时，$2x - 1\neq0$，
∴$x = 2$是原方程的解。故答案为$x = 2$。

5如图，点$A$，$B$在数轴上所对应的数分别为$-2$和$\frac{x}{x + 3}$，且点$A$，$B$到原点的距离相等，则$x$的值是__________.

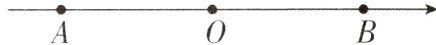
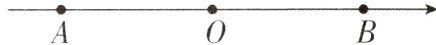
答案： -6 [解析]
∵点A，B在数轴上所对应的数分别为-2和$\frac{x}{x + 3}$，且点A，B到原点的距离相等，
∴$-2+\frac{x}{x + 3}=0$，去分母，得$-2x - 6 + x = 0$，解得$x = - 6$。检验：当$x = - 6$时，$x + 3 = - 3\neq0$，
∴分式方程的解为$x = - 6$。故答案为-6。

6解方程：(1)$\frac{x}{x + 1}+\frac{3}{x}=1$. (2)$\frac{2x}{x - 2}=1+\frac{1}{x - 2}$.

答案： [解]
(1)方程两边同乘$x(x + 1)$，得$x^{2}+3(x + 1)=x(x + 1)$，解整式方程得$x=-\frac{3}{2}$。检验：当$x=-\frac{3}{2}$时，$x(x + 1)\neq0$，
∴$x=-\frac{3}{2}$是原方程的解。
(2)方程两边同乘$(x - 2)$，得$2x = x - 2 + 1$，解得$x = - 1$。检验：当$x = - 1$时，$x - 2\neq0$，
∴$x = - 1$是原方程的解。

7关于$x$的分式方程$\frac{m}{x - 1}-\frac{2}{x - 1}=3$有增根，则$m$的值是（ ）
A. 1
B. 2
C. -1
D. -2

答案： B [解析]$\frac{m}{x - 1}-\frac{2}{x - 1}=3$，方程两边同乘$(x - 1)$，得$m - 2 = 3(x - 1)$，解得$x=\frac{m + 1}{3}$。
∵分式方程有增根，
∴$x = 1$。把$x = 1$代入$x=\frac{m + 1}{3}$中，得$1=\frac{m + 1}{3}$，解得$m = 2$，故选B。

8关于$x$的方程$\frac{x - 1}{x - 3}=2+\frac{k}{x - 3}$有增根，则增根是________，$k$的值是________.

答案： $x = 3$ 2 [解析]方程两边同乘$(x - 3)$，得$x - 1 = 2(x - 3)+k$，解得$x = 5 - k$。
∵方程有增根，
∴$x = 3$。把$x = 3$代入$x = 5 - k$中，得$3 = 5 - k$，解得$k = 2$，
∴关于$x$的方程$\frac{x - 1}{x - 3}=2+\frac{k}{x - 3}$的增根是$x = 3$，$k$的值是2，故答案为$x = 3$，2。

9解分式方程：$\frac{x + 1}{x - 1}-\frac{4}{x^{2}-1}=1$.

答案： [解]去分母，得$(x + 1)^{2}-4=x^{2}-1$，解得$x = 1$。检验：当$x = 1$时，$x^{2}-1 = 0$，
∴$x = 1$是原方程的增根，
∴原分式方程无解。

10已知关于$x$的分式方程$\frac{2}{x - 1}+\frac{mx}{(x - 1)(x + 2)}=\frac{1}{x + 2}$.
(1)若方程的增根为$x = 1$，求$m$的值；
(2)若方程有增根，求$m$的值；
(3)若方程无解，求$m$的值.

答案： [解]方程两边同乘$(x + 2)(x - 1)$，得$2(x + 2)+mx=x - 1$，移项、合并同类项得$(m + 1)x=-5$。
(1)
∵$x = 1$是分式方程的增根，
∴$1 + m=-5$，解得$m=-6$。
(2)
∵原分式方程有增根，
∴$(x + 2)(x - 1)=0$，解得$x=-2$或$x = 1$。当$x=-2$时，$m = 1.5$；当$x = 1$时，$m=-6$。综上，$m$的值为1.5或-6。
(3)当$m + 1 = 0$时，该方程无解，此时$m=-1$；当$m + 1\neq0$时，要使原方程无解，由
(2)得$m=-6$或$m = 1.5$。综上，$m$的值为-1或-6或1.5。

11对于分式方程$\frac{x - 3}{x - 2}+1=\frac{3}{2 - x}$，小明的解法如下：
解：方程两边同乘$(x - 2)$，得$x - 3+1=-3$，①
解得$x=-1$. ②
检验：当$x=-1$时，$x - 2\neq0$. ③
所以$x=-1$是原分式方程的解.
小明的解法有错误吗？如果有错误，请你指出从第几步开始出错，并写出正确的解题过程.

答案： [解]有错误，从第①步开始出错。正确的解题过程如下：方程两边同乘$(x - 2)$，得$x - 3 + x - 2=-3$，解得$x = 1$。检验：当$x = 1$时，$x - 2\neq0$。所以原分式方程的解为$x = 1$。