《2025年初中必刷题八年级数学下册苏科版》

1[2024江苏苏州虎丘区校级期中]根据下列四边形中所标的数据，一定能判定其为平行四边形的是（ ）

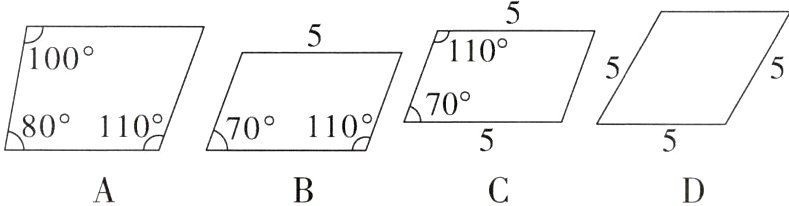
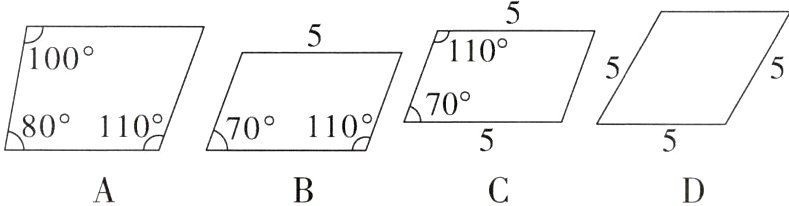
答案： C【解析】A选项，由同旁内角互补，两直线平行判定四边形上下一组对边平行，左右一组对边不平行，故四边形不是平行四边形，故A不符合题意；B选项，由同旁内角互补，两直线平行判定四边形左右一组对边平行，不能判定左右一组对边相等或上下一组对边平行，故不能判定四边形是平行四边形，故B不符合题意；C选项，由同旁内角互补，两直线平行判定四边形上下一组对边平行，结合上下一组对边相等，可以判定四边形是平行四边形，故C符合题意；D选项，四边形的左右一组对边相等，但不能判定上下一组对边相等或左右一组对边平行，故不能判定四边形是平行四边形，故D不符合题意. 故选C.

2已知四边形ABCD中，AB//CD，AB = CD，四边形ABCD的周长为40 cm，两邻边的比是3:2，则较长边的长是（ ）
A. 8 cm
B. 10 cm
C. 12 cm
D. 14 cm

答案： C【解析】$\because AB// CD$，$AB = CD$，$\therefore$四边形$ABCD$是平行四边形，$\therefore AD = BC$. 设平行四边形$ABCD$的两邻边长分别是$3x\ cm$，$2x\ cm$.$\because$平行四边形$ABCD$的周长是$40\ cm$，$\therefore 2(3x + 2x)=40$，解得$x = 4$，$\therefore$较长边的长是$3\times4 = 12(cm)$.

3[2023江苏扬州江都区期末]如图，点A，B，C，D在网格中小正方形的顶点处，AD与BC相交于点O，若小正方形的边长为1，则DO的长为________.

答案：
3【解析】如图，取一点$E$，使$CE = AB$，连接$AE$.$\because AB// EC$，$AB = EC = 2$，$\therefore$四边形$AECB$是平行四边形，$\therefore AE// BC$.$\because AD=\sqrt{3^{2}+4^{2}} = 5$，$DE = 5$，$\therefore AD = DE$，$\therefore \angle DAE=\angle DEA$.$\because AE// BC$，$\therefore \angle DAE=\angle DOC$，$\angle DEA=\angle DCO$，$\therefore \angle DOC=\angle DCO$，$\therefore DO = DC = 3$.

4[2024陕西西安校级模拟]如图，△ABC与△DEF的边BC，EF在同一条直线上，AB//DE，AC//DF且BE = CF，求证：四边形ABED是平行四边形.

答案： 【证明】$\because BE = CF$，$\therefore BE + EC = EC + CF$，即$BC = EF$.$\because AB// DE$，$AC// DF$，$\therefore \angle B=\angle DEF$，$\angle ACE=\angle F$，$\therefore \triangle ABC\cong \triangle DEF(ASA)$，$\therefore AB = DE$.又$\because AB// DE$，$\therefore$四边形$ABED$是平行四边形.

5如图，点A，F，C，D在同一直线上，AB = DE，AF = CD，BC = EF.
（1）求证：∠ACB = ∠DFE；
建议用时20分钟答案D13
（2）连接BF，CE，直接判断四边形BFEC的形状.

答案： （1）【证明】$\because AF = CD$，$\therefore AF + CF = CD + CF$，即$AC = DF$. 在$\triangle ABC$和$\triangle DEF$中，$\begin{cases}AB = DE,\\BC = EF,\\AC = DF,\end{cases}$$\therefore \triangle ABC\cong \triangle DEF(SSS)$，$\therefore \angle ACB=\angle DFE$.
（2）【解】四边形$BFEC$是平行四边形.由（1）可知，$\angle ACB=\angle DFE$，$\therefore BC// EF$. 又$\because BC = EF$，$\therefore$四边形$BFEC$是平行四边形.

6[2024四川成都模拟]如图，在四边形ABCD中，AD//BC，若添加一个条件，使四边形ABCD为平行四边形，则下列正确的是（ ）

A. AB = CD
B. AB = AD
C. ∠ADB = ∠DBC
D. ∠ABC = ∠ADC

答案： D【解析】A选项，$\because AD// BC$，$AB = CD$，$\therefore$四边形$ABCD$可能是平行四边形，也可能是等腰梯形，$\therefore$四边形$ABCD$不一定是平行四边形，故A不符合题意. B选项，$\because AD// BC$，$AB = AD$，$\therefore$四边形$ABCD$是一组对边平行且一组邻边相等的四边形，$\therefore$四边形$ABCD$不一定是平行四边形，故B不符合题意. C选项，$\because AD// BC$，$\therefore \angle ADB=\angle DBC$.$\because$只知道四边形$ABCD$有一组对边平行，$\therefore$四边形$ABCD$不一定是平行四边形，故C不符合题意. D选项，$\because BC// AD$，$\therefore \angle DBC=\angle ADB$.$\because \angle ABC=\angle ADC$，$\therefore \angle ABC-\angle DBC=\angle ADC-\angle ADB$，$\therefore \angle ABD=\angle CDB$，$\therefore AB// CD$，$\therefore$四边形$ABCD$是平行四边形，故D符合题意，故选D.

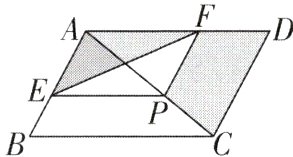
7如图，▱ABCD的面积为4，点P在对角线AC上，E，F分别在边AB，AD上，且PE//BC，PF//CD，连接EF，图中阴影部分的面积为（ ）

A. 1.8
B. 2
C. 2.4
D. 3

答案： B【解析】设$EF$交$AC$于点$O$.$\because$四边形$ABCD$是平行四边形，$\therefore AB// CD$，$AD// BC$.$\because PE// BC$，$PF// CD$，$\therefore AE// PF$，$AF// EP$，$\therefore$四边形$AEPF$是平行四边形，$\therefore S_{\triangle AEO}=S_{\triangle PFO}$，$\therefore S_{阴影}=S_{\triangle ACD}=\frac{1}{2}S_{\square ABCD}=\frac{1}{2}\times4 = 2$，故选B.

8[2024北京通州区期中]如图，在四边形ABCD中，AE⊥BD，CF⊥BD，垂足分别为E，F. 请你只添加一个条件：____________（不另加辅助线），使得四边形AECF为平行四边形.

答案： $\angle AFE=\angle CEF$(答案不唯一)【解析】添加条件$\angle AFE=\angle CEF$，理由：$\because AE\perp BD$，$CF\perp BD$，$\therefore AE// CF$.$\because \angle AFE=\angle CEF$，$\therefore AF// CE$，$\therefore$四边形$AECF$为平行四边形. 故答案为$\angle AFE=\angle CEF$(答案不唯一).

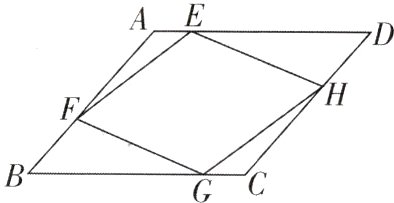
9如图，E，F，G，H分别为▱ABCD的边AD，AB，BC，CD上的点，且AE = CG，BF = DH. 求证：四边形EFGH是平行四边形.

答案： 【证明】$\because$四边形$ABCD$是平行四边形，$\therefore \angle A=\angle C$，$AB = CD$.$\because BF = DH$，$\therefore AB - BF = CD - DH$，即$AF = CH$.在$\triangle AEF$和$\triangle CGH$中，$\begin{cases}AF = CH,\\\angle A=\angle C,\\AE = CG,\end{cases}$$\therefore \triangle AEF\cong \triangle CGH(SAS)$，$\therefore EF = GH$，同理可得$\triangle BGF\cong \triangle DEH$，$\therefore FG = EH$，$\therefore$四边形$EFGH$是平行四边形.