1. 以下列长度的线段为边,不能构成三角形的是(
A.5,12,13
B.3,4,5
C.101,102,103
D.5,7,12
D
)A.5,12,13
B.3,4,5
C.101,102,103
D.5,7,12
答案:
D
2. 在下列长度的四根木棒中,能与4cm,9cm长的两根木棒首尾相接构成一个三角形的是(
A.4cm
B.5cm
C.9cm
D.13cm
C
)A.4cm
B.5cm
C.9cm
D.13cm
答案:
C
3. 如图,D是△ABC的边BC上的一点,则图中三角形个数为
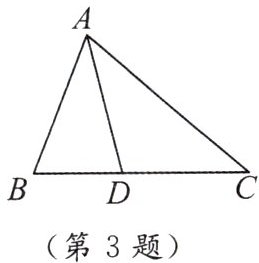
3
个.
答案:
3
4. 若△ABC中,∠A:∠B:∠C= 2:3:5,则∠A=
36°
,∠B=54°
,∠C=90°
.
答案:
$\angle A = 36^{\circ}$,$\angle B = 54^{\circ}$,$\angle C = 90^{\circ}$(按题目要求填写对应角度值即可,这里以具体值呈现答案形式)即分别填$36^{\circ}$,$54^{\circ}$,$90^{\circ}$。
5. 按角分类,下列△ABC是什么三角形?说明理由.
(1)∠A= 60°,∠C= 80°.
(2)∠B= 40°,∠C= 50°.
(3)∠A= 30°,∠C= 45°.
(1)∠A= 60°,∠C= 80°.
(2)∠B= 40°,∠C= 50°.
(3)∠A= 30°,∠C= 45°.
答案:
(1)
∵∠A=60°,∠C=80°,
∴∠B=180°-∠A-∠C=180°-60°-80°=40°.
∵∠A、∠B、∠C均为锐角,
∴△ABC是锐角三角形.
(2)
∵∠B=40°,∠C=50°,
∴∠A=180°-∠B-∠C=180°-40°-50°=90°.
∵∠A=90°,
∴△ABC是直角三角形.
(3)
∵∠A=30°,∠C=45°,
∴∠B=180°-∠A-∠C=180°-30°-45°=105°.
∵∠B=105°>90°,
∴△ABC是钝角三角形.
(1)
∵∠A=60°,∠C=80°,
∴∠B=180°-∠A-∠C=180°-60°-80°=40°.
∵∠A、∠B、∠C均为锐角,
∴△ABC是锐角三角形.
(2)
∵∠B=40°,∠C=50°,
∴∠A=180°-∠B-∠C=180°-40°-50°=90°.
∵∠A=90°,
∴△ABC是直角三角形.
(3)
∵∠A=30°,∠C=45°,
∴∠B=180°-∠A-∠C=180°-30°-45°=105°.
∵∠B=105°>90°,
∴△ABC是钝角三角形.
6. 如图,已知D,E分别为△ABC中AC,AB边上任意两点(与点A不重合),比较AB+AC与BE+DE+CD的大小,并说明理由.
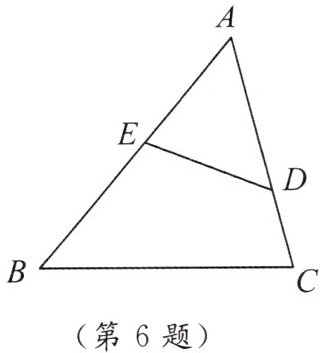

答案:
AB+AC>BE+DE+CD.
理由如下:
∵E在AB上,
∴AB=AE+BE.
∵D在AC上,
∴AC=AD+CD.
∴AB+AC=AE+BE+AD+CD.
在△AED中,根据三角形两边之和大于第三边,得AE+AD>DE.
∴AE+AD+BE+CD>DE+BE+CD,即AB+AC>BE+DE+CD.
理由如下:
∵E在AB上,
∴AB=AE+BE.
∵D在AC上,
∴AC=AD+CD.
∴AB+AC=AE+BE+AD+CD.
在△AED中,根据三角形两边之和大于第三边,得AE+AD>DE.
∴AE+AD+BE+CD>DE+BE+CD,即AB+AC>BE+DE+CD.
查看更多完整答案,请扫码查看


