《2025年期中期末名校名区真题精编高一数学上册人教版》

1. 设集合$A = \{ - 2, - 1,0,1\}$，$B = \{ x|x^{2} \lt 1\}$，则$A\cap (\complement_{\mathbf{R}}B)=$（D）
A.$\{ - 2\}$
B.$\{ 0\}$
C.$\{ - 2,0,1\}$
D.$\{ - 2, - 1,1\}$

答案： 1.D 本题考查集合的交集、补集运算 解不等式$x^2＜1$可得$B=\{x|-1＜x＜1\}$，所以$\complement_{R}B=\{x|x\leq -1或x\geq 1\}$，又$A=\{-2,-1,0,1\}$，所以$A\cap(\complement_{R}B)=\{-2,-1,1\}$.故选D.

2. 对于任意实数$a$，$b$，$c$，$d$，下列结论正确的是（B）
A.若$a^{2} \lt b^{2}$，则$a \lt b$
B.若$a \lt b$，$c \gt d$，则$a - c \lt b - d$
C.若$a + c \lt b + d$，$c \lt d$，则$a \lt b$
D.若$a \lt b$，$c \lt d$，则$ac \lt bd$

答案： 2.B 本题考查不等式的基本性质 对于A，取$a=2$，$b=-3$，满足$a^2 ＜ b^2$，但$a ＞ b$，故A错误；对于B，因为$c ＞ d$，所以$-c ＜ -d$，又因为$a ＜ b$，所以$a - c ＜ b - d$，故B正确；对于C，取$a=1$，$b=0$，$c=10$，$d=20$，满足$a + c ＜ b + d$，$c ＜ d$，但$a ＞ b$，故C错误；对于D，取$a=0$，$b=3$，$c=-5$，$d=-4$，满足$a ＜ b$，$c ＜ d$，但$ac=0$，$bd=-12$，$ac ＞ bd$，故D错误.故选B.

3. 已知幂函数$f(x) = (2m^{2} - m)x^{m - \frac{1}{2}}$在区间$(0,+\infty)$上单调递增，则$m =$（B）
A.$- 2$
B.$1$
C.$- \frac{1}{2}$
D.$- 1$

答案： 3.B 本题考查幂函数的概念、幂函数的单调性 由题意有$2m^2 - m = 1$，解得$m = 1$或$m = -\frac{1}{2}$.①当$m = -\frac{1}{2}$时，$f(x)=x^{-1}$，$f(x)$在区间$(0, +\infty)$上单调递减，不符合题意；②当$m = 1$时，$f(x)=x^{\frac{1}{2}}$，$f(x)$在区间$(0, +\infty)$上单调递增，符合题意.故选B.

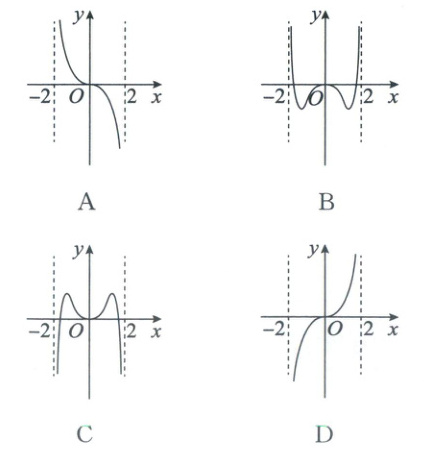
4. 函数$f(x) = x^{2}\log_{4}\frac{2 + x}{2 - x}$的大致图象是（D）

答案： 4.D 本题考查函数图象的识别 由$\frac{2 + x}{2 - x} ＞ 0$，得$(x + 2)(x - 2) ＜ 0$，所以$-2 ＜ x ＜ 2$，所以函数$f(x)=x^2\log_{4}\frac{2 + x}{2 - x}$的定义域为$(-2, 2)$，定义域关于原点对称，又$f(-x)=(-x)^2\log_{4}\frac{2 - x}{2 + x}=-f(x)$，所以函数$f(x)$是奇函数，其图象关于原点对称，排除BC；当$x\in(0, 2)$时，$\frac{2 + x}{2 - x} ＞ 1$，则$\log_{4}\frac{2 + x}{2 - x} ＞ 0$，因此$f(x) ＞ 0$，排除A.故选D.
一题多解
由第一种解法，知函数$f(x)$是奇函数，其图象关于原点对称，排除BC；因为$f(1)=\frac{1}{2}\log_{2}3 ＞ 0$，所以排除A.故选D.
规律方法
函数图象识别的三种常用方法
(1)抓住函数的性质，定性分析
①利用函数的定义域，判断函数图象左右的位置，利用函数的值域，判断函数图象上下的位置；
②利用函数的单调性，判断函数图象的变化趋势；
③利用函数的奇偶性，判断函数图象的对称性；
④利用函数的周期性，判断函数图象的循环往复；
⑤利用函数的最值判断函数图象的变化.
(2)抓住函数的特征，定量计算
注意联系基本初等函数的图象，当选项无法排除时，可代入特殊值判断.
(3)根据实际背景、图形判断函数图象
①根据题目所给条件确定函数解析式，从而判断函数图象(定量分析)；
②根据自变量取不同值时函数值的变化、增减速度等判断函数图象(定性分析).

5. 已知函数$f(x) = \begin{cases}a^{x} + 1,x \lt 1,\\ - x^{2} + (2a + 1)x - 4a + 2,x\geqslant 1\end{cases}$在$\mathbf{R}$上是减函数，则$a$的取值范围是（C）
A.$(0,\frac{1}{2})$
B.$(0,\frac{1}{2}]$
C.$[\frac{1}{3},\frac{1}{2}]$
D.$[\frac{1}{2},+\infty)$

答案： 5.C 本题考查分段函数的单调性 因为$f(x)$在$\mathbf{R}$上是减函数，所以$\begin{cases}0 ＜ a ＜ 1\frac{2a + 1}{2}\leq 1\\-1 + (2a + 1) - 4a + 2\leq a + 1\end{cases}$，解得$\frac{1}{3}\leq a\leq\frac{1}{2}$，所以$a$的取值范围是$[\frac{1}{3},\frac{1}{2}]$.故选C.

6. 荀子在《劝学》中说：“不积跬步，无以至千里；不积小流，无以成江海.”所以说学习是日积月累的过程，每天进步一点点，前进不止一小点.我们可以把$(1 + 1\%)^{365}$看作每天的“进步”率都是$1\%$，一年后是$1.01^{365} \approx 37.7834$；而把$(1 - 1\%)^{365}$看作每天的“退步”率都是$1\%$，一年后是$0.99^{365} \approx 0.0255$.若李响同学和肖济同学基础相同，从现在开始，李响同学每天“进步”$1\%$，而肖济同学每天“退步”$1\%$，经过$230$天后，李响同学的水平大约是肖济同学的（D）（参考数据：$\lg101 \approx 2.0043$，$\lg99 \approx 1.9956$）
A.$50$倍
B.$70$倍
C.$90$倍
D.$100$倍

答案： 6.D 本题考查指、对数运算 设两人现在的水平均为1，经过230天后，李响同学的水平大约是肖济同学的$t$倍.则$t=\frac{1.01^{230}}{0.99^{230}}=\frac{(101)^{230}}{(99)^{230}}$，$\lg t=\lg(\frac{101}{99})^{230}=230(\lg101 - \lg99)\approx2$，所以$t\approx100$.故选D.

7. 已知$a = 0.9^{13}$，$b = 1.3^{0.9}$，$c = \log_{2}3$，则（C）
A.$a \lt c \lt b$
B.$c \lt a \lt b$
C.$a \lt b \lt c$
D.$c \lt b \lt a$

答案： 7.C 本题考查指对数比较大小 由$0.9^{13}＜0.9^0 = 1$，得$a ＜ 1$，由$1.3^{0.9}＞1.3^0 = 1$，$1.3^{0.9}＜1.3^1 = 1.3$，得$1 ＜ b ＜ 1.3$，由$1.5=\log_{2}\sqrt{8}＜\log_{2}\sqrt{9}=\log_{2}3$，得$c ＞ 1.5$.故$a ＜ b ＜ c$.故选C.

8. 已知函数$f(x) = \frac{e^{x} - 1}{e^{x} + 1}$，若对任意的正数$a$，$b$，满足$f(a) + f(2b - 2) = 0$，则$\frac{2}{a} + \frac{1}{b}$的最小值为（4）
A.$2$
B.$4$
C.$6$
D.$8$

答案： 8.B 本题考查基本不等式及其应用、函数的奇偶性与单调性
思路探寻：先判断函数$f(x)$的单调性和奇偶性，利用基本不等式求$\frac{2}{a}+\frac{1}{b}$的最小值. 乘法展开$a + 2b = 2$
对任意的$x\in\mathbf{R}$，$e^x + 1 ＞ 0$，所以函数$f(x)=\frac{e^x - 1}{e^x + 1}$的定义域为$\mathbf{R}$，关于原点对称.因为$f(-x)=\frac{e^{-x} - 1}{e^{-x} + 1}=\frac{e^x(e^{-x} - 1)}{e^x(e^{-x} + 1)}=\frac{1 - e^x}{1 + e^x}=-f(x)$，所以函数$f(x)$为奇函数.因为$f(x)=\frac{e^x + 1 - 2}{e^x + 1}=1-\frac{2}{e^x + 1}$，且函数$y = e^x + 1$在$\mathbf{R}$上为增函数，所以函数$f(x)=\frac{e^x - 1}{e^x + 1}$在$\mathbf{R}$上为增函数.因为对任意的正数$a$，$b$，满足$f(a)+f(2b - 2)=0$，所以$f(a)=-f(2b - 2)=f(2 - 2b)$，所以$a = 2 - 2b$，即$a + 2b = 2$，所以$\frac{2}{a}+\frac{1}{b}=\frac{1}{2}(a + 2b)(\frac{2}{a}+\frac{1}{b})=\frac{1}{2}(4+\frac{a}{b}+\frac{4b}{a})\geq\frac{1}{2}[4 + 2\sqrt{\frac{a}{b}·\frac{4b}{a}}]=4$，当且仅当$\begin{cases}\frac{a}{b}=\frac{4b}{a}\\a + 2b = 2\\a ＞ 0\\b ＞ 0\end{cases}$，即$\begin{cases}a = 1\\b=\frac{1}{2}\end{cases}$时，等号成立，故$\frac{2}{a}+\frac{1}{b}$的最小值为4.故选B.